Ch 3 - Exponential and Logarithmic Functions

sequence

function from the whole number to the real number

arithmetic sequence

a(n) = a(0) + dn

common difference

a(n) = a(k) + d(n - k)

geometric sequence

g(n) = g(0) * r^h

common ratio

g(n) = g(k) * r^(h-k)

arithmetic creates _______ while geometric create ________

linear functions; exponential functions

linear function based on table bc

equal length input value intervals have output values of function change at a constant rate

exponential

consistent ration that is multiplied between equa distant input intervals

rate of change is increasing when

concave up (quadratic) or going up (exponential)

rate of change is decreasing when

concave down (quadratic) or going near asymptote (exponential)

exponential function parts

f(x) = a * b ^(x - c) + d

a = vertical stretch or compression

b = base

c = horizontal shift

d = vertical shift

reflect over x-axis when (-) negative is in front of

a

reflect over y-axis when (-) negative is in front of

x

increasing at an increasing rate

f(x) = e^x

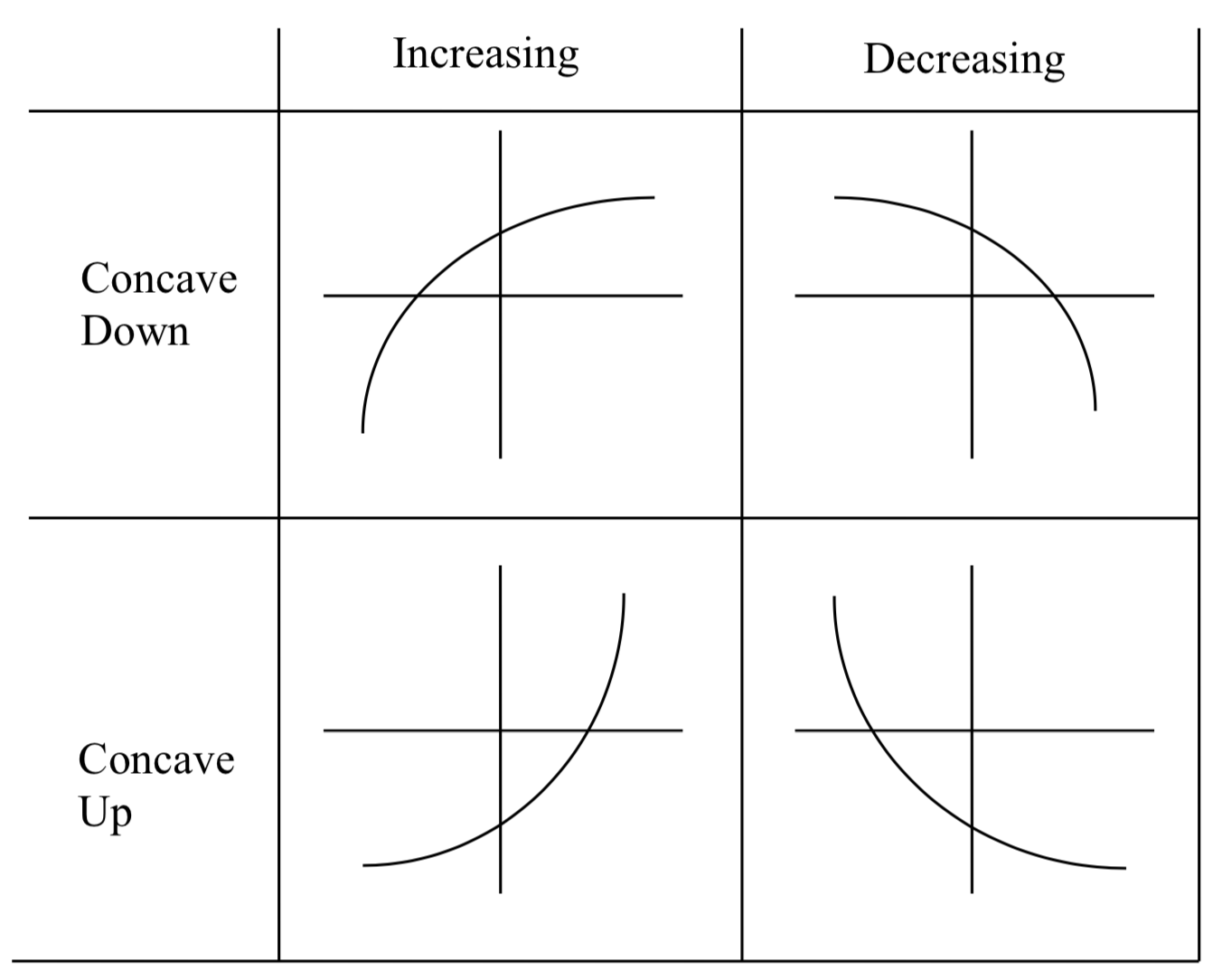
increasing at a decreasing rate

f(x) = e^-x

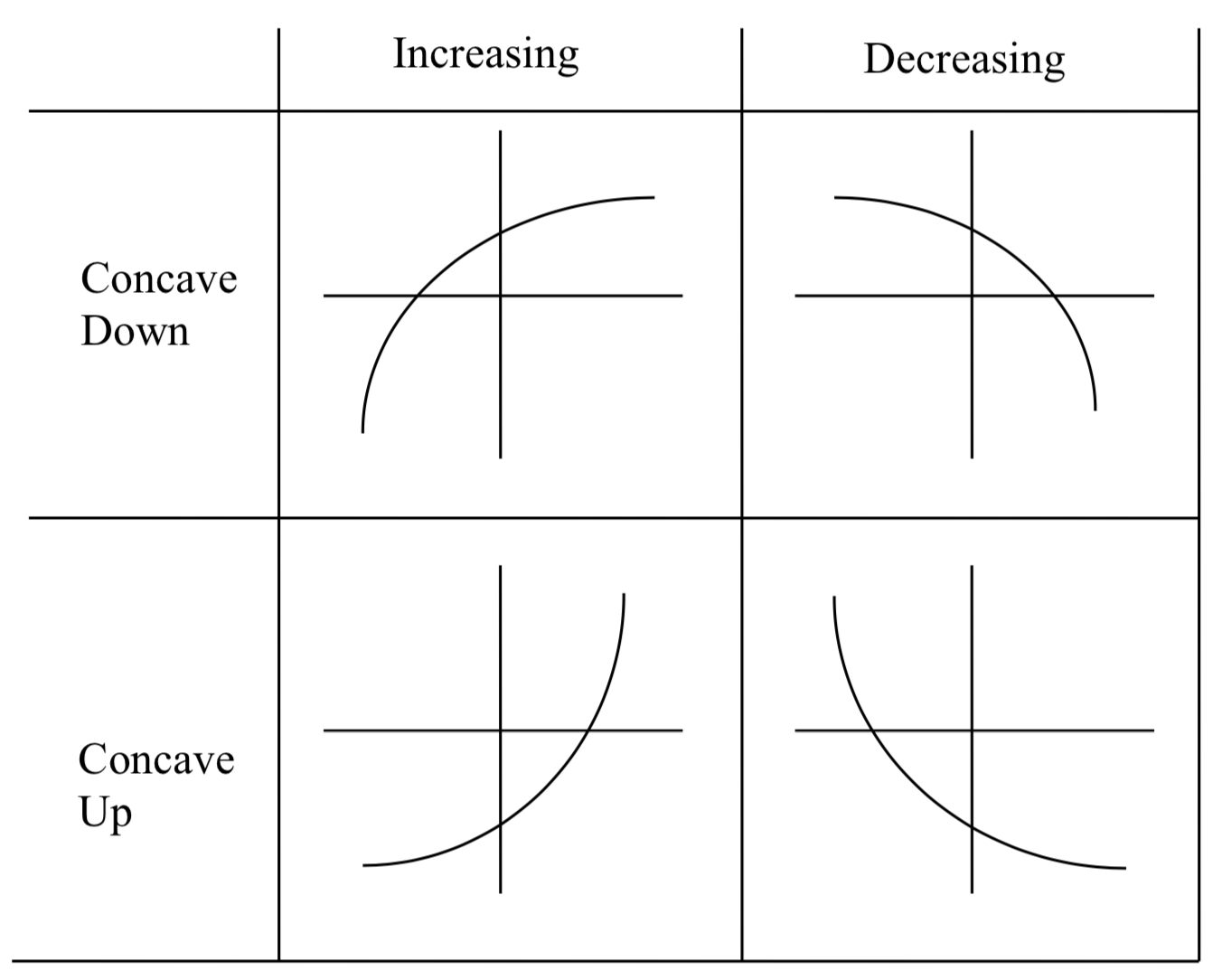
decreasing at a decreasing rate

f(x) = -e^x

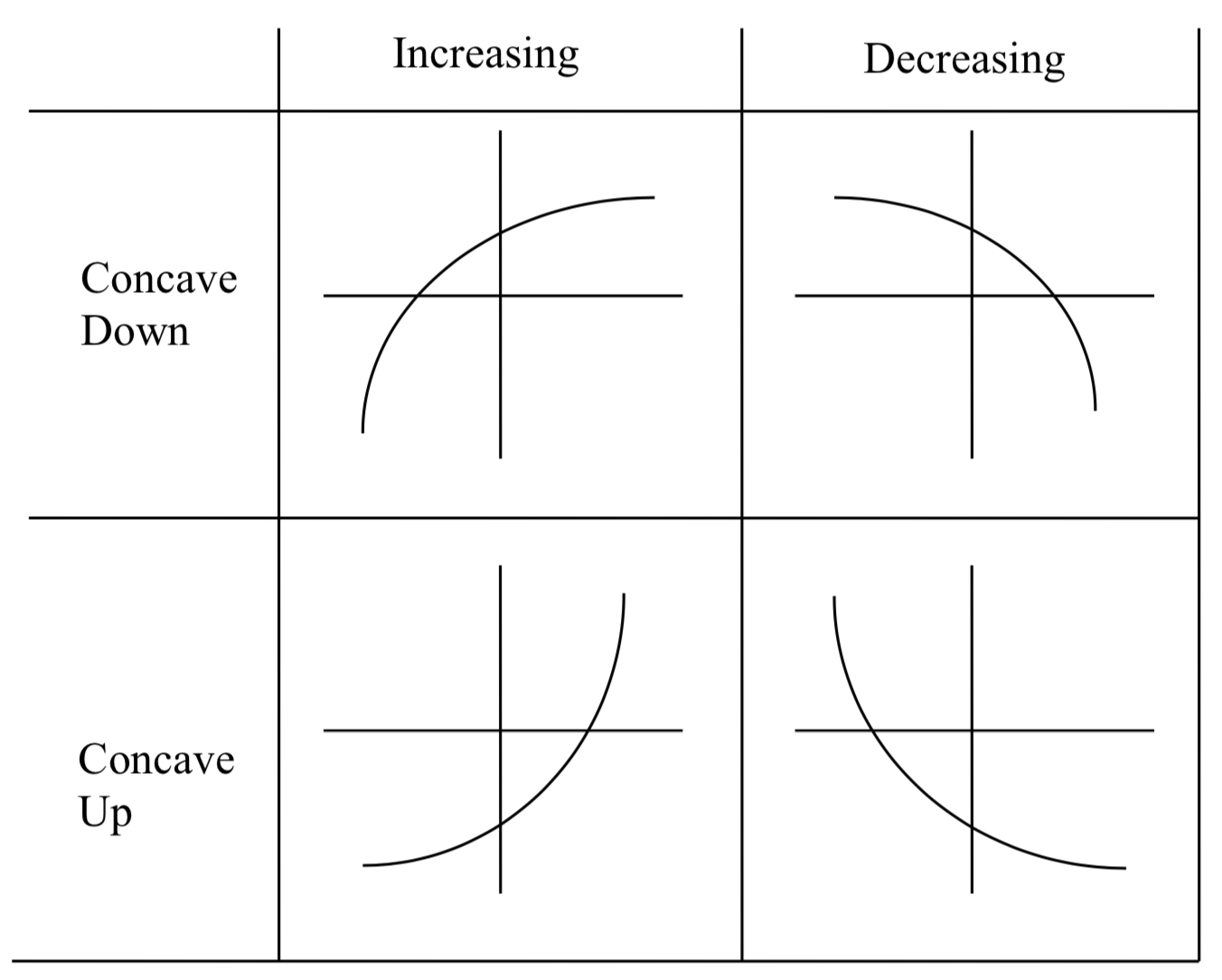
decreasing at an increasing rate

f(x) = -e^-x

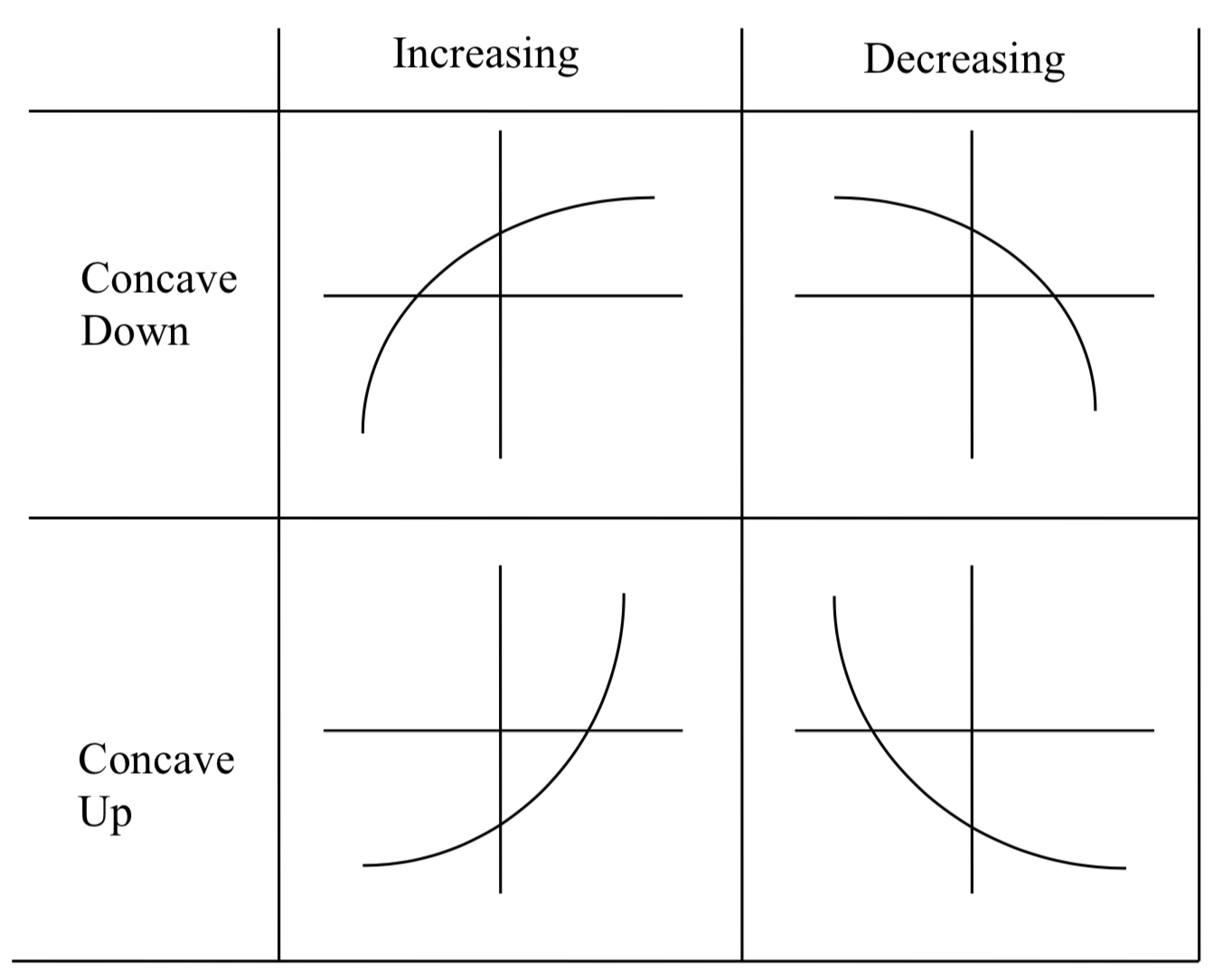
vertical stretch or compression

stretch = a > 1

compress/shrink = 0 < a < 1

half life formula

A = P (1/2) ^ t/h

compound interest

A = P (1 + r/n) ^ nt

compound continuous

A = Per^rt

logarithmic function

y = log(b) * (x - h) + k; vertical asymptote = h

log(a) 1 = 0 means

a^0 = 1

log(a) a = 1 means

a^1 = a

inverse property

log(a) a^x = x means a^log(a)x = x

one to one property

log(a) x = log(a) = y means x= y

for logs and ln, what must x always be

x > 0

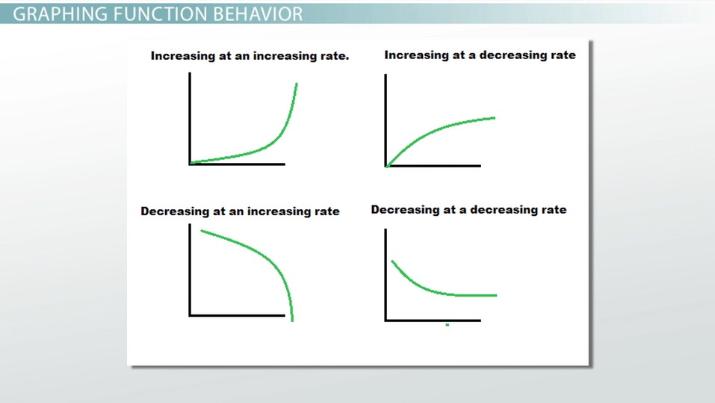
increasing at a decreasing rate

f(x) = -ln(x)

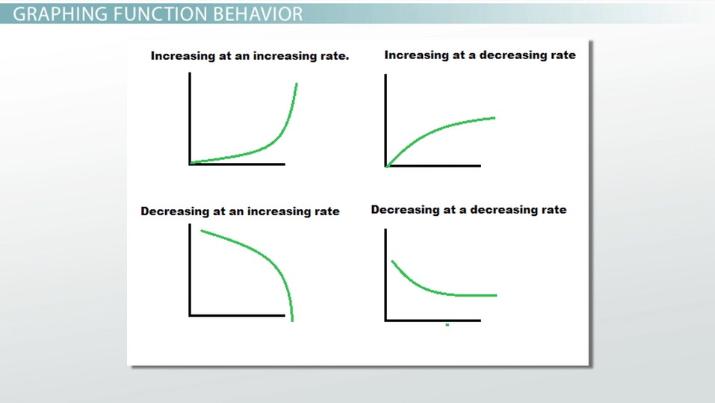
decreasing at an increasing rate

f(x) = ln (-x)

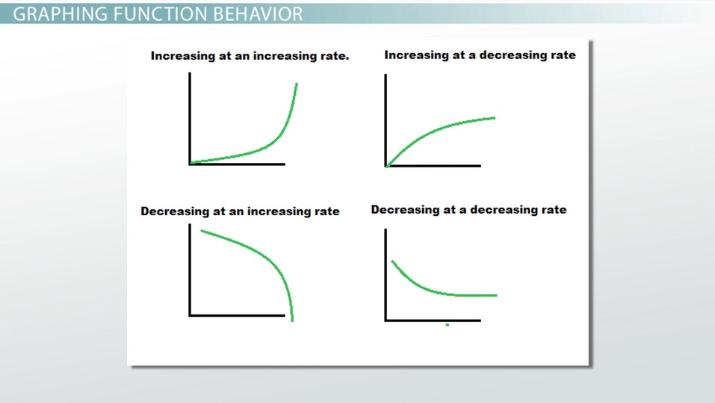
increasing at an increasing rate

f(x) = -ln (-x)

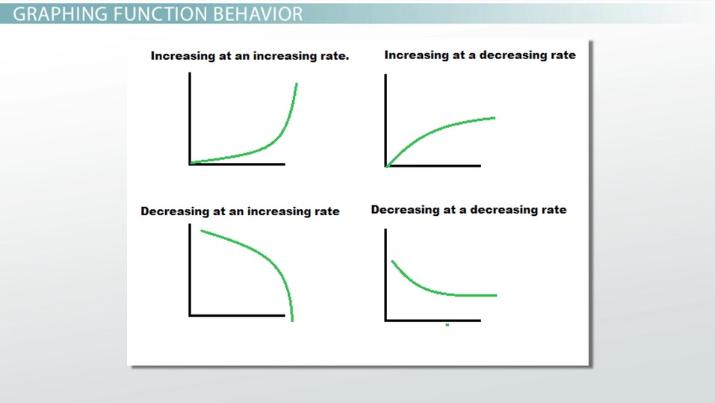
decreasing at a increasing rate

f(x) = ln (x)

ln (-x+3)

reflect across the y-axis at x = 3

-x +3 > 0 = x < 3

change of base formula

log (a) x = log x / log a

product property of logs

log (a) uv = log (a) u + log (a) v

quotient property of logs

log (a) u/v = log (a) u - log (a) v

log power property

log (a) u^v = v log (a) u

gaussian model

y = ae^-(x-b)² / c

logistic model

y = a/ 1 + be^-rx

exponential model regression

y = a * b^x

coefficient of determination

r² ; measure that provides information about goodness of fit of a model; closer to 0.99 is best fit

correlation coefficient

r ; defined correlation between independent and depend variables between -1 and + 1;

power model regression

y = a * x^b

LnReg - Logarithmic Model

y = a + b ln x

LinReg - Linear Model

y = ax + b