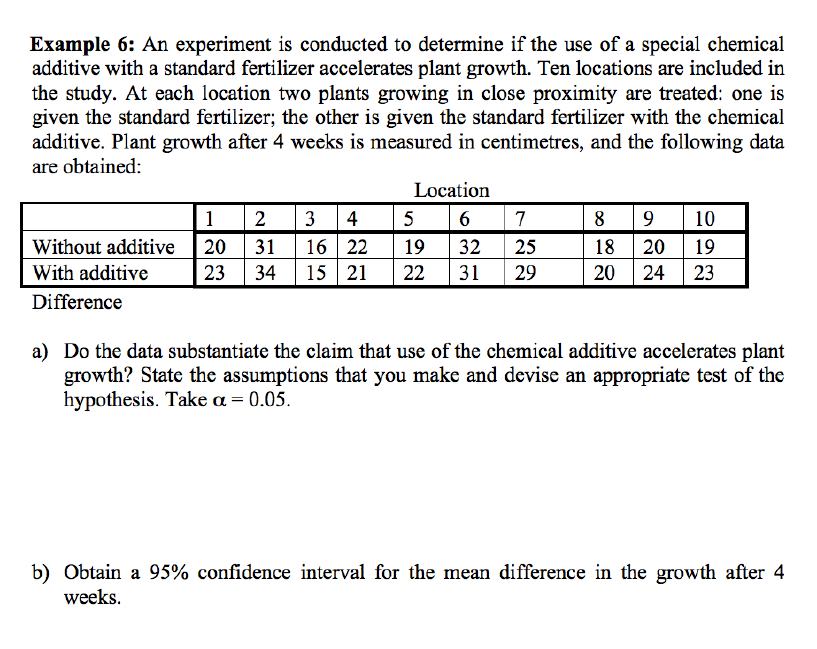
week 8 - Introduction to Confidence Intervals & Hypothesis Testing and Comparing Two Means

explain a 95% confidence interval

on average, 95% of the confidence intervals contain mu - success rate rate of the procedure

what is the general structure of a confidence interval for a known sigma? draw a distribution to illustrate a 90% CI

as the level of confidence increases, what happens to the width of the interval? why is this the case?

• as the level of confidence increases, the interval becomes wider

• this is because the only thing changing is the multiplier - as level of confidence increases, multiplier also increases

what 3 factors must you consider when trying to determine the required sample size?

how do you achieve a smaller margin of error (d)?

lower level of confidence, thus lower z multiplier

how do you calculate the appropriate sample size given a desired accuracy and margin of error?

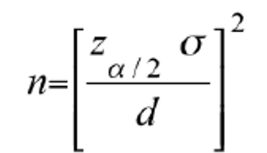
why do we tend to use wider intervals and a larger n when sigma is unknown?

to account for the extra variability from using s rather than sigma

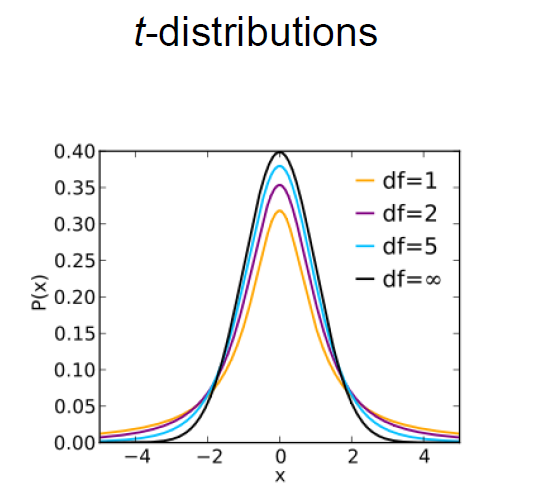
describe the features of t distributions. what are the differences between t distributions and the normal distribution and when does the t dist = the normal dist?

• longer tails thus give larger CIs - harder to reject H0

• does not have a fixed width - changes depending on the sample size

• normal dist is a single curve, t dist is a family of curves that changes with df

• when df = infinity, you get the normal distribution

define a 95% confidence interval for mu with an unknown sigma

• a) iv - success rate of procedure

• b) all employees of the company near you

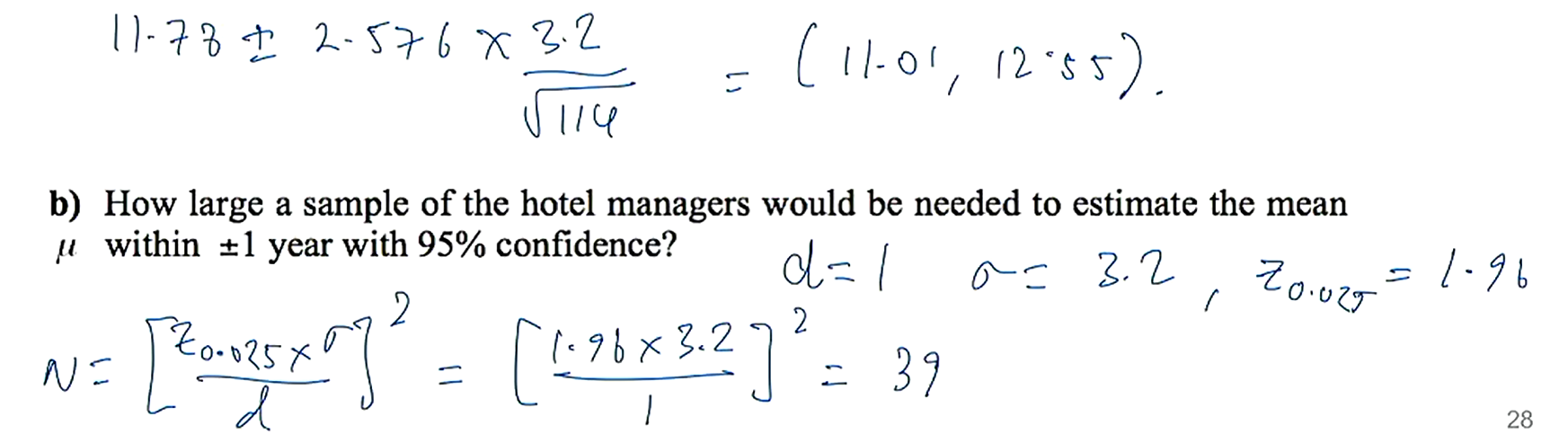
define the test statistic for a known sigma

when is there a relationship between confidence intervals and tests of significance?

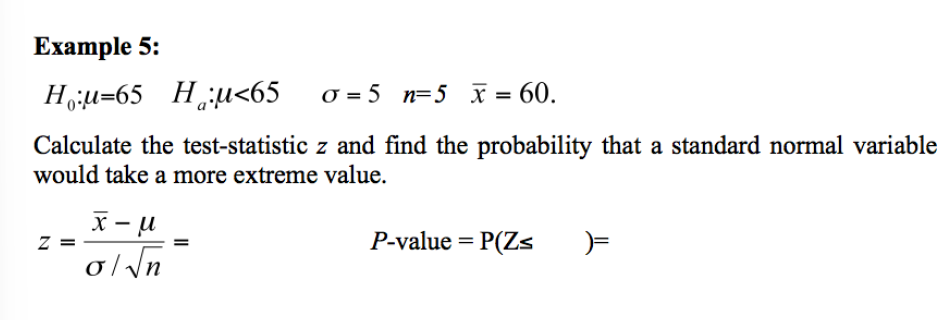
no answer?

p between 0.1, 0.2 (2 sided)

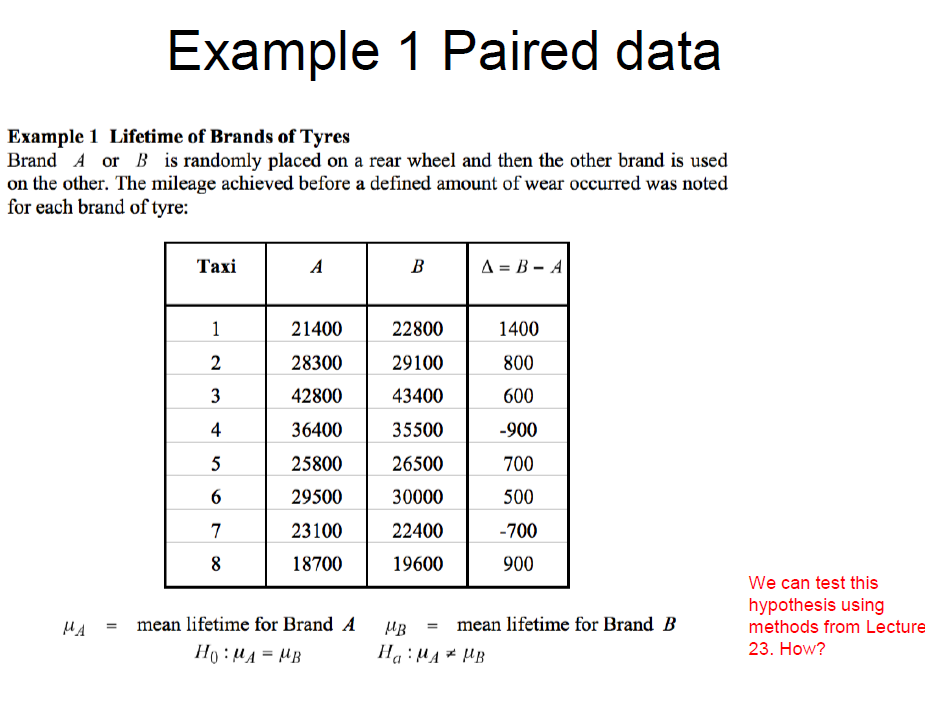
we are finding the prob that men will have a higher average, thus X1 (females) - X2 (males) will be negative → we are finding the prob that Z is less than a certain value

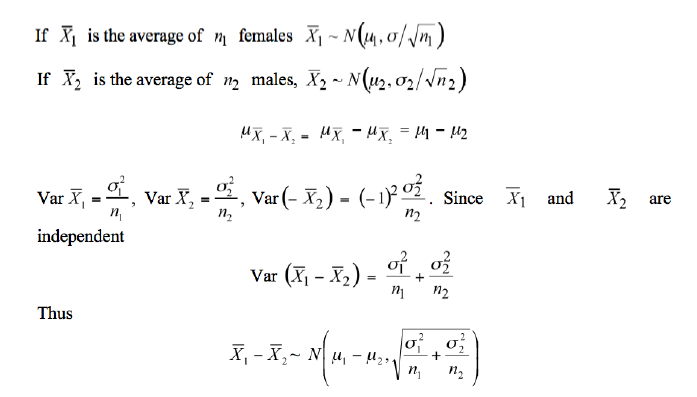
explain these calculations

• we can take the means of the differences, as the expectation of the differences is simply X1-X2

• we can find SD by adding the expected variances. each independent variance = SD^2/n

• thus, SD of each independent sample is sqrt (SD^2/n). we can add the SDs as they are independent (E(X1-X2))

how do you calculate the 2 sample Z statistic? how is the 2 sample t statistic different to this?

t statistic using s rather than sigma

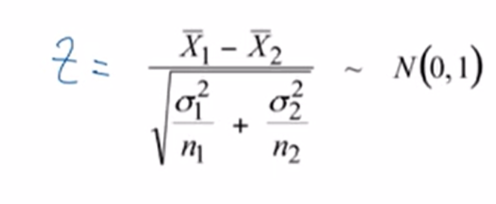
how do you construct a confidence interval for a 2 sample t test?

we want to know if zero is within the confidence interval

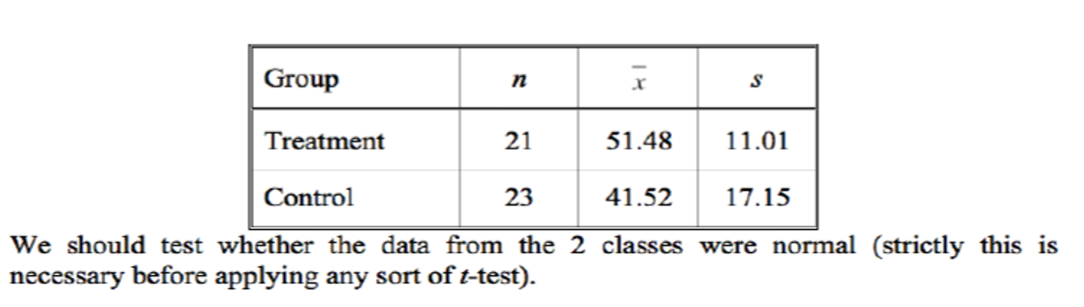
does the treatment group result in a significantly larger mean?