F6

15.4

Modellantaganden

Modeller bygger på antaganden. Exempelvis bygger hypotestest/konfidensintervall på antagande om normalfördelning

• Om antagandet inte håller kan du inte lita på delarna eller resultatet

Om antagandena stämmer har OLS-skattningen två bra egenskaper

• Den är unbiased, dvs 𝐸 (𝑏j) = Bj

• Den har minsta variationen mellan stickprov

• pålitlig och exakt - ”Gauss-Markov-teoremet”

Om något av dessa antaganden inte stämmer blir modellen fel

1 Modellen är linjär i parametrarna (koefficenterna) och korrekt specificerad

Förändringen i y är lika stor vid en förändring i x oavsett värdet på x

• det är en rät linje

• x värden kan kvadreras men inte koefficenterna. Koefficenterna förändras ej och är samma för lika x-värden

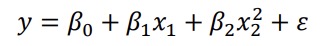
”Modellen ska innehålla allt det den ska innehålla”

Modellen är linjär i parametrarna och har additivt fel ε

Varför problem?

• Om det verkliga sambandet inte är linjärt borde vi få olika koefficienter för olika värden på x

Hur upptäcka?

• Residualplot: scatterplot av residualer mot x-variabler - mönster?

Lösning?

• använd icke-linjär metod

• transformera variablerna

• “utöka modellen” - svårt att göra ny enkänt

2 Det finns ingen multikolinjäritet

Inget tydligt samband mellan olika x-variabler

• Om 𝑥1ökar när 𝑥2 ökar, hur ska vi då mäta varifrån förändringen i y kommer?

• Viss samvariation finns alltid men får ej vara för stark (korrelation över 80%). Ju lägre desto bättre

Hur upptäcker vi? Skattade koefficenter

• har fel tecken

• har stora standardfel = är inte statistiskt signifikanta

• Högt R2 och signifikant modell samtidigt som skattade koefficienter inte är signifikanta

Vad gör vi?

• Ta bort en av de korrelerade variablerna - modellen kan bli sämre

• skaffa större stickprov

• Transformera någon av de korrelerade variablerna (avstånd i kvadrat) = för att bryta det linjära sambandet

3 Homoskedasticitet

Vi antar att spridningen bland residualerna är densamma (runt nollvärdet) oavsett värde på x

• Om detta inte stämmer (heteroskedasticitet) har vi problem

Varför problem?

• Inte med skattade koefficienter (de är rätt!) men

• Standardfelen blir felaktigt uppskattade och därav kan inte t- eller F-test användas

Hur upptäcka?

• Scatter plot över residualer mot x-variabel eller predikterade yvärden

• 

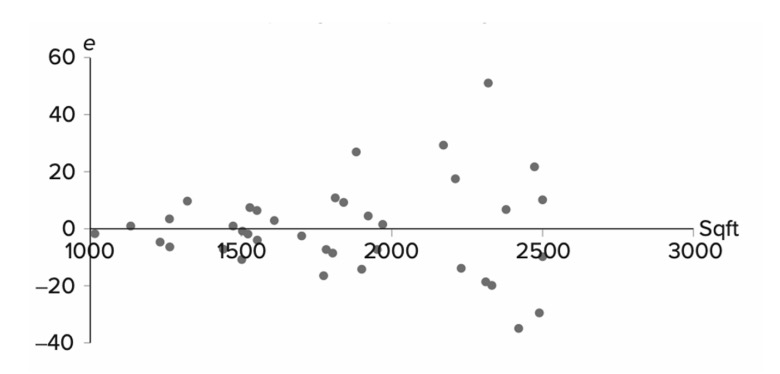
Vad ska vi göra?

• konstaterar problem kan man förhålla sig till dem

• skattade koefficienter stämmer men standardfel och därav t.test eller F-test kan bli felaktiga

4 Ingen autokorrelation (”serial correlation”)

Observationer av feltermen är okorrelerade

• Feltermerna är inte slumpmässiga utan systematiska

• Skattade koefficienter är dock fortfarande unbiased

Varför problem?

• Standardfelen blir underskattade

• Felaktigt högt R2

• Felaktig signifikans

Hur upptäcka?

• Scatter plot med residualer över tid - mönster = problem

5 Ingen endogenitet

Att feltermen inte är korrelerad med någon av de oberoende variablerna

• Om korrelation finns är de oberoende variablerna faktiskt inte oberoende

Viss korrelation förekommer ofta

• Om korrelationen är för stor får vi problem

• Beror vanligen på att det finns förklaringsvariabler som vi missat

• omitted variables

Varför problem?

• Vi kan inte lita på de skattade koefficienterna

• omitted variable bias

Hur upptäcka? Att vi kan lita på att vi fått med det som behövs i modellen

Vad göra? Se till att ha en så bra modell som möjligt

6 Normalfördelade residualer

Förutsätter att små avvikelser är vanligare än stora och att fördelningen är symmetrisk

Varför problem?

• Om residualerna inte är normalfördelade kan vi inte lita på våra konfidensintervall eller hypotestest

Hur upptäcka?

• Histogram över feltermerna

Vad göra?

• Använda tillräckligt stora stickprov

• Använda mer avancerade metoder

Att testa antagandena

• Vi kan inte testa alla antaganden

• Det vi kan testa utgår från analys av residualerna

• Vi kan inte observera den faktiska feltermen 𝜀 eftersom den bara finns i populationen men vi kan se och mäta residualerna e = y-ytak

• Bra första steg: scatter plot av residualer mot a) förklaringsvariablerna, b) predikterade värden (ytak)