geometrie - teil 1

Satz Innenwinkelsumme im Dreieck

In jedem Dreieck beträgt die Summe der Innenwinkelgrößen 180 Grad.

Beweis IWS Dreieck

Es sei ABC ein Dreieck mit den Eckpunkten A, B und C und es seien α, β und γ die Größen der Innenwinkel bei A, B bzw. C . Wir betrachten die Parallele h zur Geraden g = AB durch den Punkt C . Es sei A′ ein Punkt auf h derart, dass A′ nicht in der gleichen Halbebene bezüglich der Geraden BC liegt wie A. Weiter sei B′ ein Punkt auf h derart, dass B′ nicht in der gleichen Halbebene bezüglich der Geraden AC liegt wie B .

Bild

Dann sind ∠BAC und ∠B ′CA Wechselwinkel an den Parallelen g und h. Nach dem Wechselwinkelsatz gilt daher |∠B ′CA| = |∠BAC | = α.

Weiter sind ∠CBA und ∠BCA′ ebenfalls Wechselwinkel an den Parallelen g und h. Nach dem Wechselwinkelsatz gilt daher |∠BCA′| = |∠CBA| = β.

Die Punkte B‘, C und A′ liegen in dieser Reihenfolge auf der Geraden h, weswegen ∠B ′CA′ ein gestreckter Winkel ist und daher |∠B ′CA′| = 180◦ gilt. Andererseits ergänzen sich die Winkel ∠B ′CA, ∠ACB und ∠BCA′ zum Winkel ∠B ′CA′.

Folglich gilt 180 Grad = |∠B ′CA′| = |∠B ′CA| + |∠ACB | + |∠BCA′| = α + γ + β.

Erster Strahlensatz

Zwei verschiedene Strahlen mit gemeinsamen Anfangspunkt O werden beide durch zueinander parallele Geraden in von O verschiedenen Punkten geschnitten. Dann verhalten sich die von O aus gemessenen Abschnittslängen auf dem einen Strahl wie die von O aus gemessenen Abschnittslängen auf dem anderen Strahl.

Genauer: Wenn A und B die Schnittpunkt der ersten Geraden mit den beiden Strahlen und A′ und B ′ die Schnittpunkt der zweiten Geraden mit den beiden Strahlen (in gleicher Reihenfolge) sind, dann gilt |AO| : |A′O| = |BO| : |B ′O|.

Beweis 1. Strahlensatz

Satz des Pythagoras

In jedem rechtwinkligen Dreieck ist das Hypothenusenlängenquadrat gleich der Summe aus den Kathetenlängenquadraten.

Beweis Satz des Pythagoras

Sphärische Geometrie

Definition Induktives Schließen

Meint das Schließen vom Besonderen auf das Allgemeine.

• typisch für Naturwissenschaften und and. nicht-math. Wissenschaften

• Vorgehen: Beobachtung spezieller Phänomene, Erkennen von Gemeinsamkeiten zwischen den Phänomenen, Verallgemeinerung als (hypothetische) Theorie

• Bsp.: viele reale Dreiecke betrachten, Innenwinkelgrößen ausmessen und addieren → Ergebnis: IWS ca. 180 Grad, wobei Abweichungen als Messfehler interpretiert werden → Behauptung: IWS 180 Grad

• Theorien können nicht bewiesen werden → daher Ziel der Wiederlegung von Theorien durch Experimente

• Bsp.: nach sphärischer Geometrie existieren reale Dreiecke mit IWS > 180 Grad → Satz der IWS nicht allgemein gültig

Def. Deduktives Schließen

• Meint das Schließen vom Allgemeinen auf das Besondere

• typisches Schließen in Mathematik

• es ex. kleine Auswahl an als wahr angenommenen Aussagen → Axiome

• auf Grundlage der Axiome wird durch logisches Schließen auf weitere wahre Aussagen geschlossen

• Axiome so gewählt, dass man mit ihnen naturwiss. Phänomene beschreiben (Theorien) kann

• solche Theorien heißen mathematische Modelle

• Modelle müssen keinen Bezug zur Realität haben

Die Elemente von Euklid

• stellen Grundlagen der euklidischen Geometrie dar

• von Euklid von Alexandria ca. 360 bis 280 v.Chr. entwickelt

• unterscheidet zwischen Definitionen, Axiomen und Postulaten

Was sind die Definitionen nach Euklid?

1. Was keine Teile hat, ist ein Punkt.

2. Eine Länge ohne Breite ist eine Linie.

3. Die Enden einer Linie sind Punkte.

4. Eine Linie ist gerade, wenn sie gegen die in ihr befindlichen Punkte auf einerlei Art gelegen ist.

5. Was nur Länge und Breite hat, ist eine Fläche.

Was sind die Axiome nach Euklid?

1. Dinge, die demselben Dinge gleich sind, sind einander gleich.

2. Fügt man Gleichem Gleiches hinzu, so sind die Summen gleich.

3. Nimmt man von Gleichem Gleiches weg, so sind die Reste gleich.

4. Was zur Deckung miteinander gebracht werden kann, ist einander gleich.

5. Das Ganze ist größer als sein Teil.

Was sind die Postulate nach Euklid?

1. Es soll gefordert werden, dass sich von jedem Punkte nach jedem Punkte eine gerade Linie ziehen lasse.

2. Ferner, dass sich eine begrenzte Gerade stetig in gerader Linie verlängern lasse.

3. Ferner, dass sich mit jedem Mittelpunkt und Halbmesser ein Kreis beschreiben lasse.

4. Ferner, dass alle rechten Winkel einander gleich seien.

5. Endlich, wenn eine Gerade zwei Geraden trifft und mit ihnen auf derselben Seite innere Winkel bildet, die zusammen kleiner sind als zwei Rechte, so sollen die beiden Geraden, ins Unendliche verlängert, schließlich auf der Seite zusammentreffen, auf der die Winkel liegen, die zusammen kleiner sind als zwei Rechte.

Kritik an den Elementen von Euklid

• nicht umfassend genau

• Definitionen sind im strengen Sinn keine Definitionen, weil Neues nicht durch Bekanntes definiert wird

• Postulate stellen die eigentlichen geometrischen Aussagen und Axiome der Geometrie dar

Moderne Axiomensysteme der euklid. Geometrie (Begriffe, Kategorien von Aussagen und Ziele)

• gehen auf David Hilbert (19.-20. Jahrhundert) zurück

• unterscheidet zwei Arten von Begriffen:

  1. undefinierte Grundbegriffe, deren Inhalte durch Axiome bestimmt wird

  2. definierte Begriffe, die auf Basis der Grundbegriffe definiert werden

• unterscheidet zwei Kategorien von Aussagen:

  1. Axiome (unbewiesene Grundaussagen)

  2. Sätze (Aussagen, die auf logischen Weg aus Axiomen abgeleitet werden können)

Ziele:

1. Axiomensystem soll widerspruchsfrei sein

2. soll minimal sein (kein Axiom aus anderen ableitbar)

3. soll vollständig sein

Definition Inzidenz

Symmetrische Relation (I) zwischen Punkten und Geraden sowie zwischen Geraden und Punkten.

Inzidenzaxiom 1 (Inz-1)

Zu je zwei voneinander verschiedenen Punkten aus der Punktmenge P gibt es genau eine Gerade aus G, die mit den beiden Punkten inzidiert.

∀A ∈ P ∀B ∈ P \{A}∃=1 g ∈ G : g | A ∧ g | B .

Inzidenzaxiom 2 (Inz-2)

Zu jeder Geraden aus G gibt es zwei verschiedene Punkte aus P, die mit dieser Geraden inzidieren.

∀g ∈ G ∃A ∈ P ∃B ∈ P \{A}: A | g ∧ B | g

Inzidenzaxiom 3 (Inz-3)

Es existieren drei paarweise verschiedene Punkte aus P, die nicht mit der gleichen Gerade aus G inzidieren.

∃A,B,C ∈ P : (A # B ∧ B # C ∧ A # C )∧ (∀g ∈ G : A ̸ | g ∨ B ̸ | g ∨ C ̸ | g).

→ #: ungleich

→ /|: inzidieren nicht

Definition Inzidenzgeometrie

Das Tripel (P, G, |) heißt Inzidenzgeometrie, wenn die Axiome Inz-1 bis 3 erfüllt sind.

Definition schneidende Geraden

Wir nennen zwei Geraden g und h einander schneidend, falls es einen Punkt P gibt, der mit beiden Geraden inzidiert. Den Punkt P nennen wird dann Schnittpunkt von g und h.

Inzidenzaxiom 0 (Inz-0)

Jede Gerade aus G ist eine Menge von Punkten aus der Punktemenge P. Ein Punkt inzidiert mit einer Geraden genau dann, wenn er Element dieser Geraden ist.

G ⊆ 2^P, ∀P ∈ P∀g ∈ G : P | g ⇐⇒ P ∈ g.

Definition P liegt auf g/ g verläuft durch P

Ein Punkt P aus P liegt auf der Geraden g aus G, wenn P mit g und damit g mit P inzidiert. Eine Gerade g verläuft durch einen Punkt P, wenn P mit g und damit g mit P inzidiert.

Definition Kollinearität

Es sei M ⊂ P eine Menge von Punkten. Die Menge M bzw. die Punkte in M heißen kollinear, falls es eine Gerade g gibt, mit der alle Punkte aus M inzidieren, also M ⊆ g gilt.

Definition Verbindungsgerade

Die Gerade, welche mit den verschiedenen Punkten A und B inzidiert, heißt Verbindungsgerade von A und B und wird mit AB bezeichnet.

Satz identische Punkte/Geraden

1. Für alle Geraden g und h aus G und alle Punkte P und Q aus P, welche auf g und h liegen, gilt: Wenn g ̸= h gilt, dann gilt P = Q.

   Umgangssprachlich: Zwei verschiedene Geraden aus G haben höchstens einen Punkt gemeinsam.

2. Für alle Geraden g und h aus G und alle Punkte P und Q aus P, welche auf g und h liegen, gilt: Wenn P ̸= Q gilt, dann gilt g= h.

   Umgangssprachlich: Liegen zwei verschiedene Punkte beide auf zwei Geraden, dann sind diese Geraden gleich.

Da 2. Kontraposition zu 1. reicht Beweis von 2.:

• Nach Inz-1 ex. genau eine Gerade aus G, die P und Q enthält. Daher muss es sich bei g und h um dieselbe Gerade handeln.

Satz Teilmenge von Gerade

Für alle Geraden g aus G und alle Teilmengen h von g gilt: Wenn h eine Gerade ist, dann gilt h= g.

Umgangssprachlich: Wenn eine Gerade Teilmenge einer Geraden ist, dann sind diese Geraden gleich zueinander.

Beweis: !!!!!

Affines Inzidenzaxiom 1

Zu je zwei voneinander verschiedenen Punkten aus P gibt es genau eine Gerade aus G, die mit den beiden Punkte inzidiert.

Affines Inzidenzaxiom 2 (Aff-2)

Zu jeder Geraden aus G gibt es zwei verschiedene Punkte aus P, die mit dieser Geraden inzidieren.

Affines Inzidenzaxiom 3 (Aff-3)

Es existieren drei paarweise verschiedene Punkte aus P, die nicht mit der gleichen Geraden aus G inzidieren.

Affines Inzidenzaxiom (Aff-3)

Es existieren drei paarweise verschiedene Punkte aus P, die nicht mit der gleichen Geraden aus G inzidieren.

Affines Inzidenzaxiom 4 (Aff-4)

Es gibt eine Äquivalenzrelation || auf G.

Affines Inzidenzaxiom 5 (Parallelenaxiom)

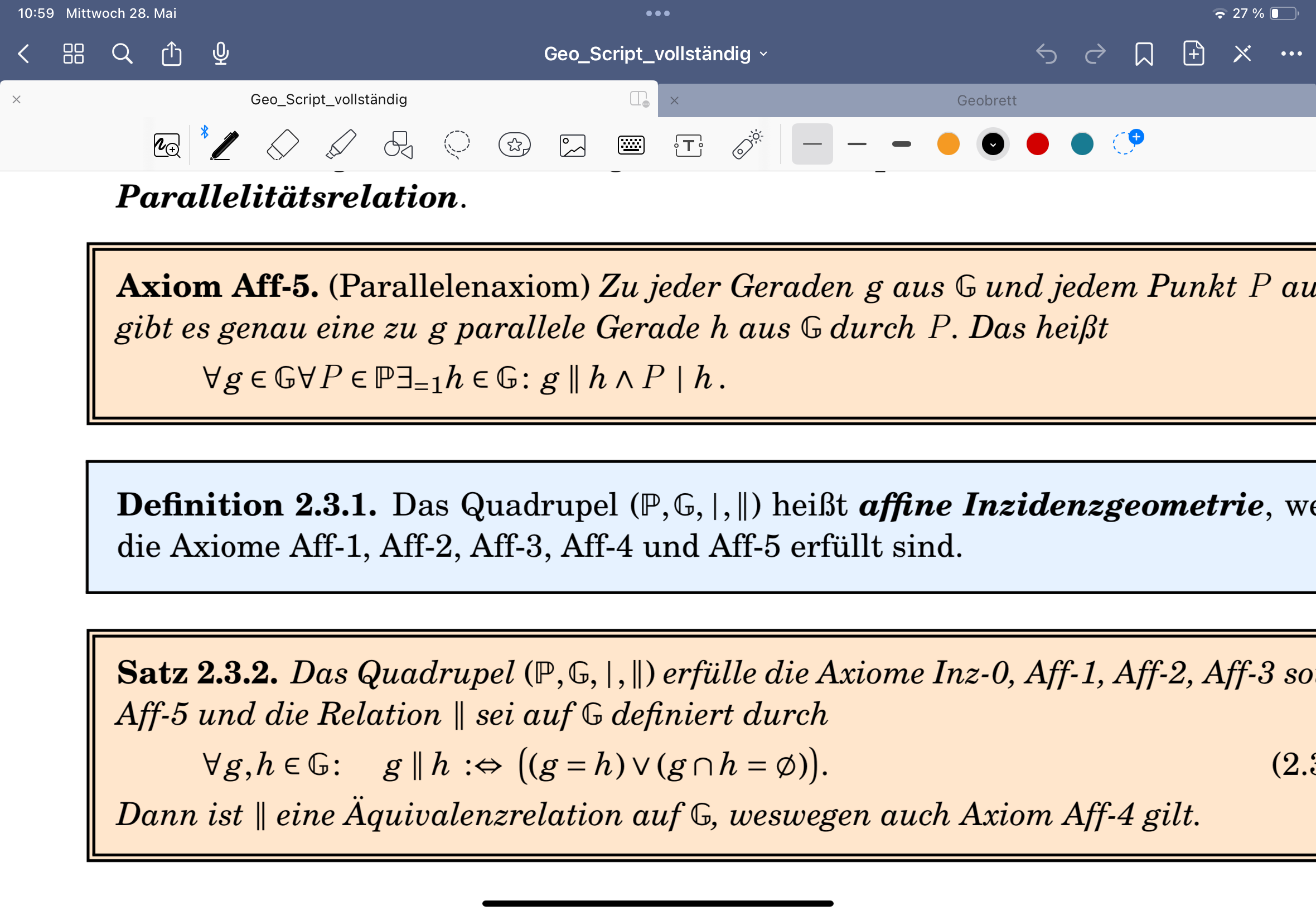
Definition affine Inzidenzgeometrie

Das Quadrupel (P, G, | , ↓) heißt affine Inzidenzgeometrie, wenn die Axiome Aff-1, Aff-2, Aff-3, Aff-4 und Aff-5 erfüllt sind.

Satz affine Inzidenzgeometrie

Das Quadrupel (P, G, | , ||) erfülle die Axiome Inz-0, Aff-1, Aff-2, Aff-3 sowie Aff-5 und die Relation || sei auf G definiert durch

∀g,h ∈ G : g ∥ h :⇔ (g= h)∨ (g ∩ h =leere Menge)).

Dann ist || eine Äquivalenzrelation auf G, weswegen auch Axiom Aff-4 gilt.

Beweis Satz: Unter den Axiomen Aff-1, ff-2, Aff-3, Aff-4 und Aff-5 gilt für alle Geraden

g, h und k aus G: Wenn g || h und g /|| k gelten, dann gilt auch h /|| k.

Zeichen /||: nicht parallel.

Es seien g, h und k Geraden aus G mit g || h und g /|| k. Angenommen, es

gilt h || k. Wegen der Transitivität der Parallelität folgt dann im Widerspruch zur

Voraussetzung g || k.

Projektive Inzidenzgeometrie (Inz-1