Pressure

Open to Atmosphere

(1)

p(y)A

(2)

h

(3)

Δm

(4)

Fluid

(5)

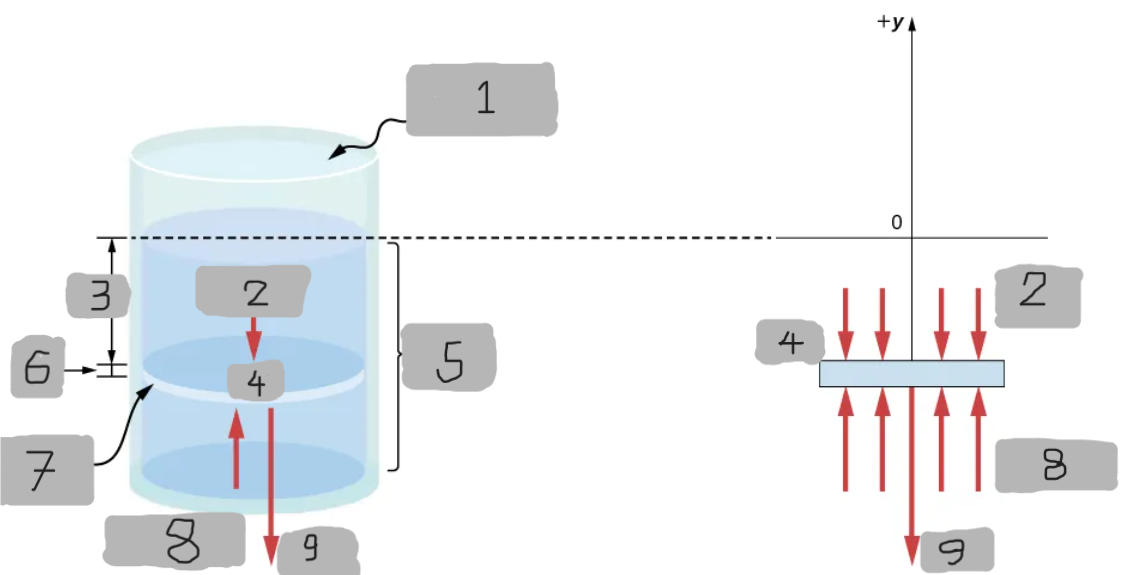
Δy

(6)

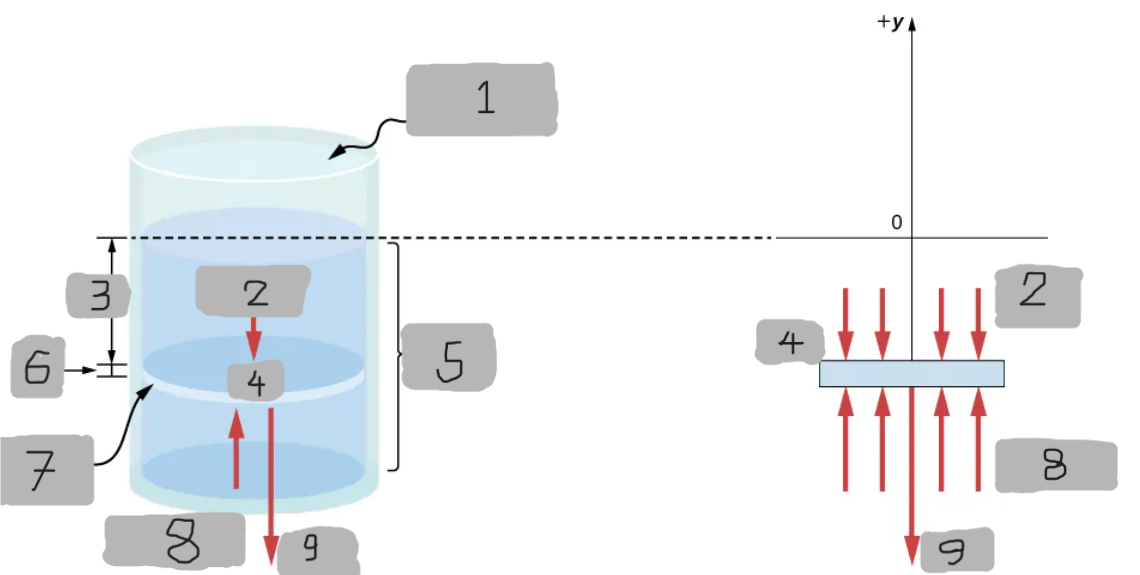
Area, A

(7)

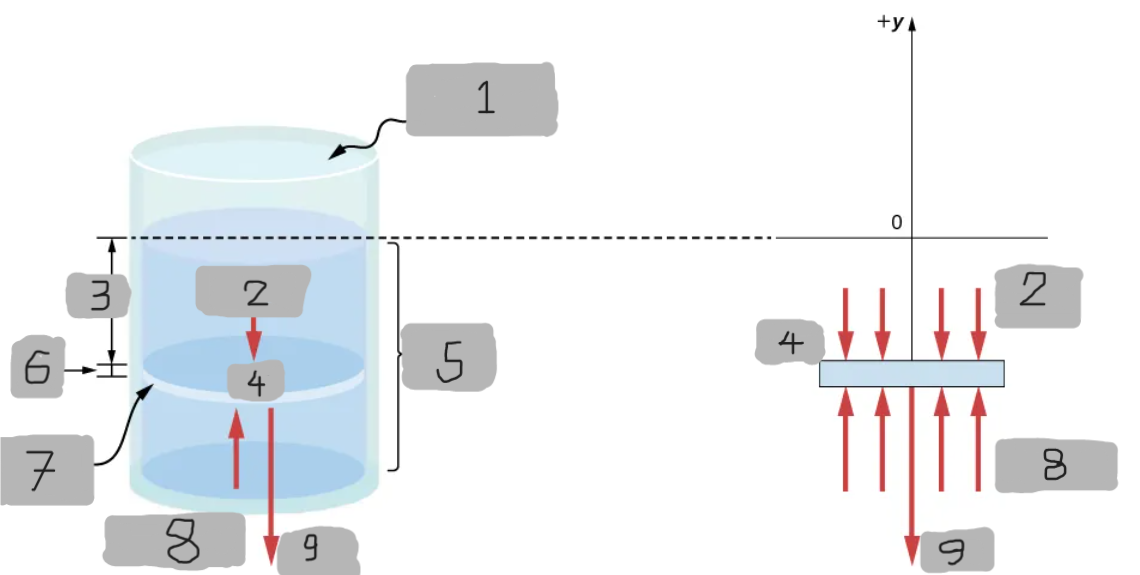
p(y + Δy)

(8)

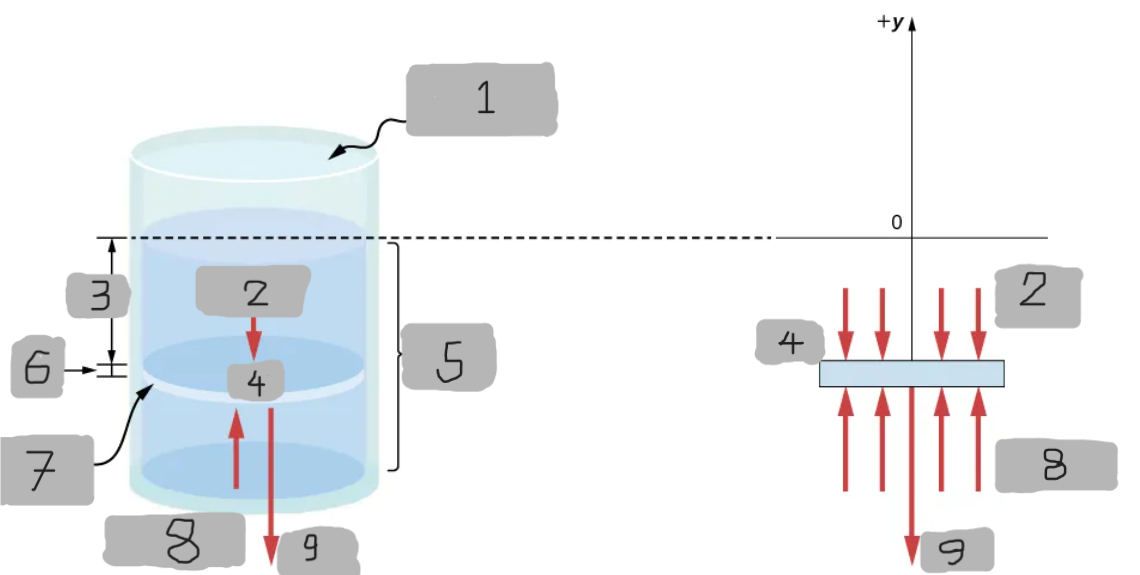
(Δm)g

(9)

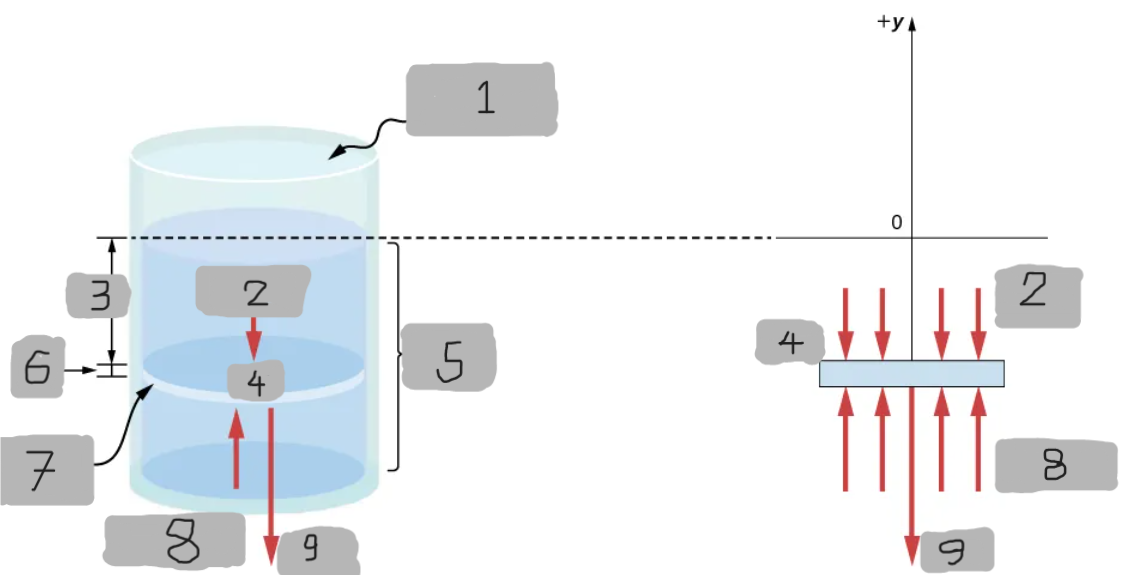
p(y)

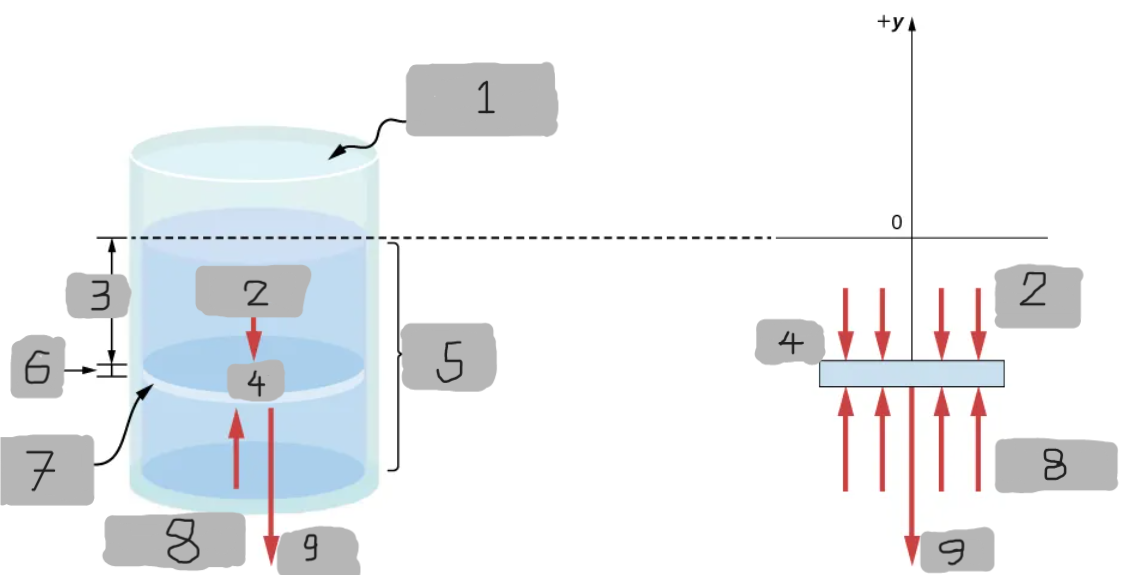
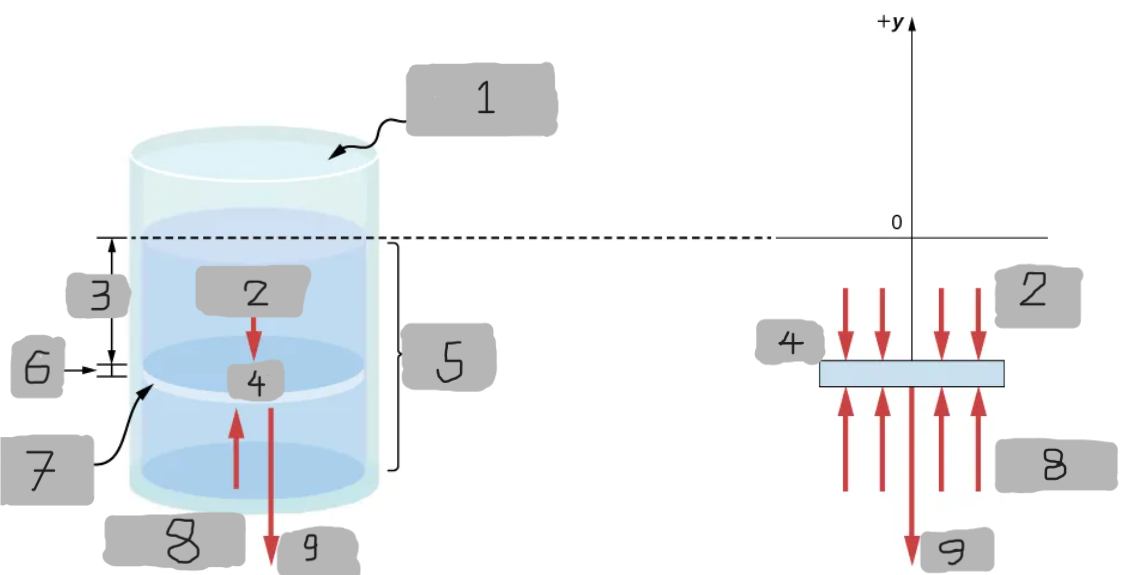
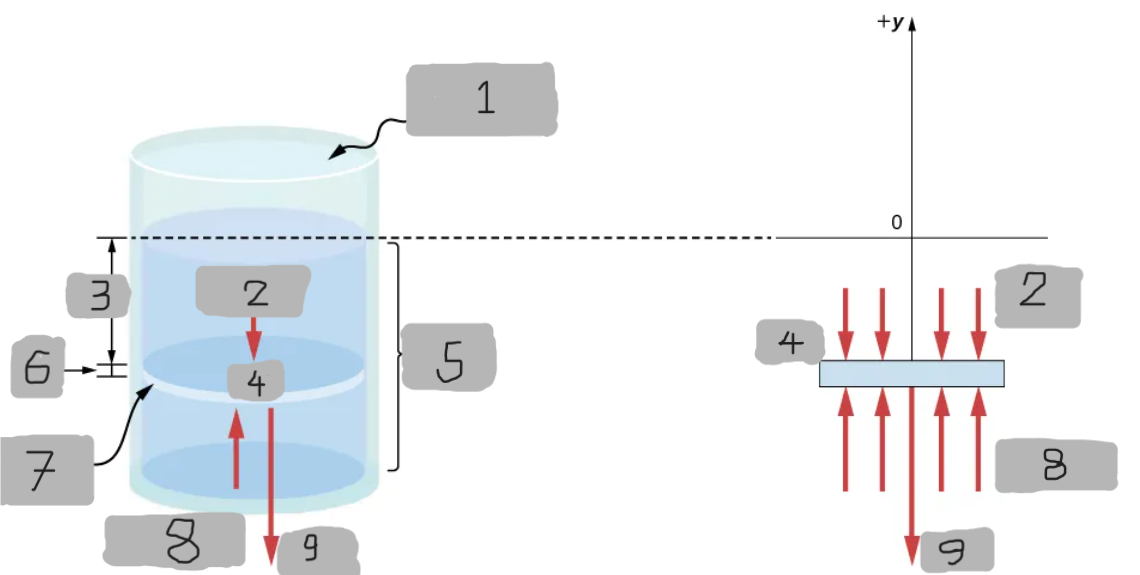
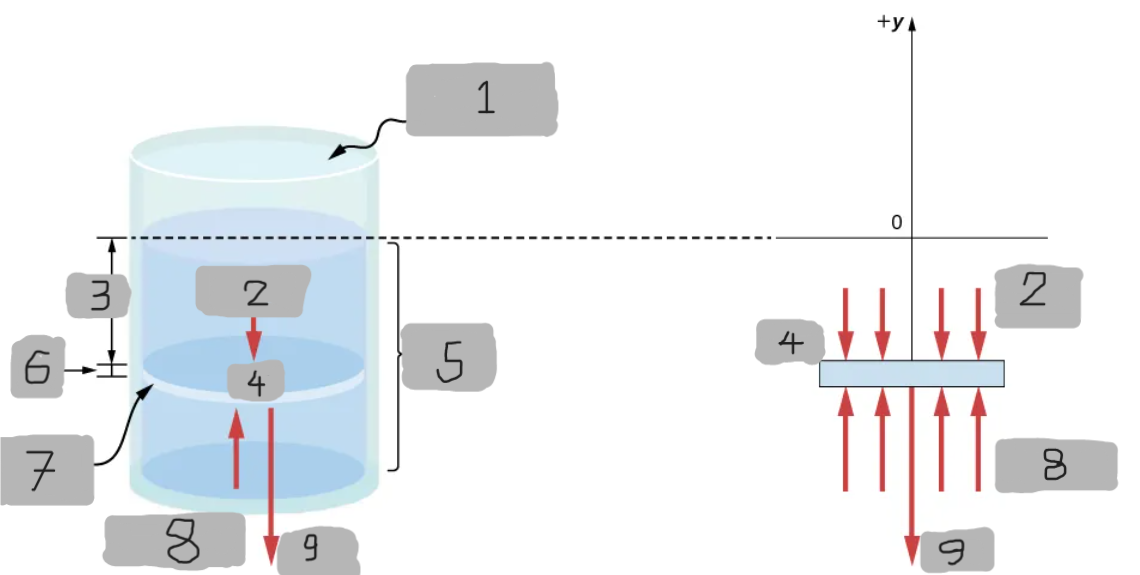
Represents all the forces acting upon the element from above.

p(y + Δy)

Represents all the forces acting upon the element from below.

y, y + Δy

Since the element of the fluid between _ and ______ is not accelerating, the forces are balanced.

p(y + Δy)A - p(y)A - gΔm = 0(Δy < 0)

Equation for the y-component using the Cartesian y-axis oriented upwards.

For the static case.

Basically Newton’s 2nd law with acceleration = 0 (static fluid)

The right hand side becomes mass × y-acceleration, instead of zero.

What happens to the force balance equation if the fluid element has a non-zero y-acceleration?

Δm = ρ × Volume

How can a mass of a small fluid element can be expressed?

AΔy, where A is the cross-sectional area and Δy is thickness.

What’s the volume of a thin fluid element?

Δm = |ρAΔy| = -ρAΔy (for Δy < 0)

Formula for the mass of fluid element in terms of ρ, A, and Δy?

[p(y + Δy) - p(y)]/Δy = -ρg

Equation that we get after substituting Δm equation into Newton’s second law equivalent equation, and then dividing both of that equation’s sides by AΔy

dp/dy = -ρg

The differential equation that we obtain by taking the limit of the infinitesimally thin element Δy → 0.

The equation represents the rate of change of pressure with depth in a fluid being proportional to the fluid’s density.

Whether the density ρ is constant or varies with the depth ρ(y)

What does solving dp/dy = -ρg depends on?

When the range of depth being analyzed is not too great, such as in most liquids like water.

When is it reasonable to assume constant density?

When depth is large enough for density to vary significantly, as in the atmosphere.

When can density not be assumed constant?

y = 0

(i)

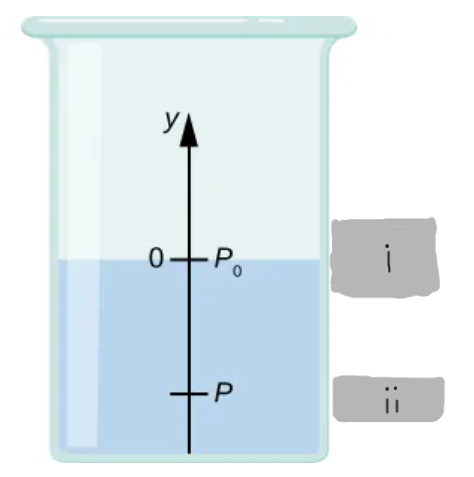
y = -h

(ii)

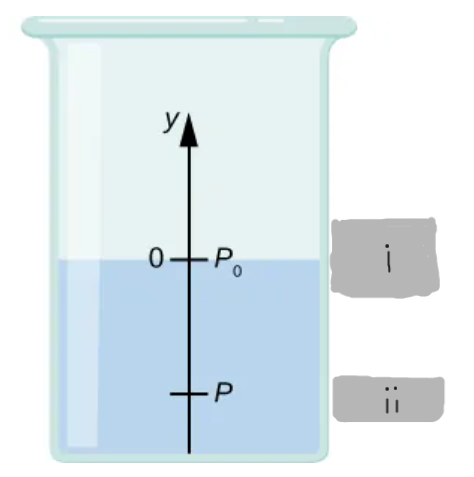
At y = 0, where pressure is atmospheric pressure p0.

At what reference point is the pressure defined in a fluid column?

∫[from p0 to p] dp = - ∫[from 0 to -h] ρg dy

What’s the pressure equation applied between y = 0 and y = -h?

p - p0 = ρgh

What’s the result of evaluating the pressure integral?

p = p0 + ρgh

What’s the final expression for pressure at depth h?

It determines how pressure decreases with altitude and is especially useful for studying the atmosphere.

Why is the change in atmospheric pressure with height important?

Air temperature is constant, and atmosphere approximately behaves like an ideal gas.

What assumptions are made when deriving pressure variation with height

p(y)

Symbol that represents the atmospheric pressure at height y in the atmosphere.

p = ρ(kBT/m)

Equation that explains how does the ideal gas law connect pressure and density in the atmosphere?

1.38 × 10^-23 J/K

Value of the Boltzmann’s constant (kB)

In terms of density ρ instead of volume V, showing that if pressure p changes, with height, density also changes.

How is the ideal gas law written in this derivation?

dp/dy = -(mg/kBT)p

What’s the differential equation for pressure variation with height

α

The symbol replaced with the constant (mg/kBT) to simplify the equation

∫(from p0 to p(y)) dp/p = ∫(from 0 to y) -α dy

How is the equation separated for the integration?

ln(p) - ln(p0) = -αy

Integrated result before simplification

p(y) = p0*e^-αy

Final expression for pressure as a function of height

Atmospheric pressure variation with height

Atmospheric pressure decreases exponentially as altitude increases above sea level.

Pressure scale height (1/α)

The characteristic length over which atmospheric pressure decreases by a factor of 1/e

Value of α at 300 K (nitrogen molecule approximation)

α = mg/kBT ≈ 1/8800 m

Physical meaning of scale height (8800m)

For every 8800 m of altitude pressure falls to about 1/3 of its original value

Limitations of constant-T, constant-g model

It provides only a rough estimate since both temperature and gravity vary with altitude

Nature of pressure

pressure is a scale of quantity having magnitude, but no direction

Direction of pressure forces

Always exerted perpendicular to surface because fluids cannot withstand shear

Pressure on tank walls

Exerted perpendicular to the inside surface at all points

Pressure on objects in fluids

Exerted perpendicular to all surfaces with greater pressure at deeper points

Net vertical force on a swimmer

Equal to the upper buoyant force minus the swimmer’s downward weight