Linear Equations, Matrices (Chapter 11, 12, 13, 14)

linear eqn is of the form

a1x1 + a2x2 + . . . + anxn = b

ai and b are real numbers (scalars) and xi are unknowns/variables/indeterminants

linear system

collection of linear eqns

solution to a linear system

• solution to ALL eqns of the system simultaneously

general solution

set of all solutions; may be infinite solutions presented w parameters

linear system is consistent when

there exists at LEAST one soln; otherwise the system is inconsistent

linear system is homogenous if

all the CONSTANT TERMS (terms w/o variables) = 0, otherwise the linear system is inhomogenous

types of general solutions

• no solution

• a unique solution

• infinite solutions (could be w parameters)

gaussian elimination

• method for solving linear systems systematically

• involves elementary row operations

• using an AUGMENTED matrix

valid operations on an AUGMENTED MATRIX

1. add a MULTIPLE of a row to another

2. exchange two rows in the matrix

3. multiply a row by a NON-ZERO scalar

homogeneous systems will always

have at least one solution, therefore homo systems are always consistent

~

“now equivalent to”

REF (row echelon form)

1. all zero rows (if any) are at the BOTTOM

2. first non-zero entry in each ROW is a 1 (CALLED A LEADING 1 OR A PIVOT)

3. each leading 1/pivot is to the R of the leading 1s of the rows above

reduced row echelon form

• like REF, except the only non-zero entry in each COLUMN is a pivot (each column has one 1 and the rest are 0)

if a row is ever [ 0 0 0 | a ] and a is non-zero,

the system is inconsistent

we say that two linear systems are equivalent if

they have the same general solution.

Two matrices A is row equivalent to B, written A ∼ B if

B can be obtained from A by elementary row operations

Any matrix can be turned into RREF via elementary row operations. Furthermore,

the RREF we get is unique.

steps to reduce linear system to REF

1. interchange the top row w another if it is needed tro bring a non-zero entry to the first row of the left-most column

2. scale R1 to get a pivot (the 1 is left most)

3. Eliminate the rest of the left-most column using the pivot in R1

4. now ignore the 1st row and repeat steps 1→ 3 w next row until you get REF

steps to reduce linear system to RREF

• first do steps to reduce to REF

• if the right-most pivot is in R1, stop

• start w right-most pivot and use to eliminate every entry above it in its column

• go to next column and go back to the first step here

to make parametric forms of general solutions

• set the non-pivot columns to parameter variables and put in para form

rank of a matrix A is denoted

rank(A)

rank(A)

number of pivots in any REF of matrix A

• the conversion from REF to RREF does not change the number of pivots

if matrix A has rank(A), then an augmented matrix with A is

B = [A|b] w b as a column vec, which has its own rank as rank(B) or rank(A|b)

rank(B) is always ____________ rank(A)

greater than or equal to

if rank(B) > rank(A), the system is

inconsistent

if rank(A) = rank(B), the system is

consistent

2 cases of rank(A) = rank(B)

1. rank(A) = number of unknowns → system has a unique solution

2. rank(A) < number of unknowns → system has infinite solutions

rank(A) is always _____________ number of unknowns

less than or equal to

traffic flow network of one-way street

then convert to REF form and make parametric eqns for each variable

scenarios for traffic network: minimum flow along road

• the constant in eqn with the road variable (xi)

scenarios for traffic network: closing a road

• set the relevant variable to 0

traffic network constraints

• one way streets, therefore xi >= 0

• 0 <= parameter variable <= smallest constant in system

• if the solution after setting a variable to 0 (solve for parameter first and then solve for all the other variables) is all positive, then there are no traffic jams

solving systems w parameters

• augmented matrix has coeffs that are variables

• to be consistent, they must be values that allow rank(A) to equal rank(A|b)

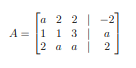
what are all the vectors that are a linear combination of [insert span of vectors]

1. start w/ x1(v1) + x2(v2) + x3(v3)

2. put into augmented matrix [A|b] with b as [a, b, c] (but vertical)

3. reduce to REF

4. and det the conditions a, b, c must be so that rank(A) = rank(A|b)

different ways to think of matrices

• a table of numbers

• the augmented matrix of a linear system

• a collection of column vectors

• a collection of row vectors

• a mathematical object in its own right

a matrix w ‘m’ rows and ‘n’ columns is called an

m by n matrix, with size m x n

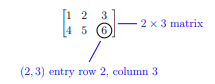
matrix notation entry

go down vertical 2, then go right 3

adding matrices and scalar mult

• and you have a zero matrix of ANY SIZE

matrix transpose

• if A is m x n then A-transpose is n x m and the rows of A are the columns of A-transpose

transpose operation on matrices satisfies

matrix product

matrix A of size m x n and matrix B of size n x p, their product is size m x p

expressing linear system as a matrix eqn

Ax = b where x and b are a column vecs and A is a matrix

expressing linear combo as a matrix multiplication

if AB = 0, ________ A or B has to be the zero-matrix

neither

ways matrix mult is diff from num mult

• AB ≠ BA (could be true in rare cases)

• AB = 0, and neither A or B has to be the zero matrix

• if AB = AC, you can’t cancel out A to get B = C

identity matrix

• denoted as Ik (k is a subscript) for k x k matrix

• has 1’s on diagonal (top left to bottom right)

• matrix product of a matrix of size n x k with an identity matrix of size k x k gives back the original matrix itself BECAUSE THE IDENTITY MATRIX IS A MULTIPLICATIVE IDENTITY

properties of matrix product

if matrix has size m x m, it is a square matrix. given a square matrix and a pos exponent integer ‘n’:

A^n = A*A*A*A*A … *A (n times)

• find the pattern by getting the product of the first few patterns'

• recognize if it produces the identity matrix

• use exponent rules

expressing linear system w ‘n’ unknowns with matrices

x = [x1, x2, …..] or x = [x, y, z] or x = [a, b, c]

and the variables in x are the variables for each column of the matrix

let A be a matrix of size m x n, Col(A) =

subspace in Rm generated by the columns of A

• column space of A

Ax = b is consistent if and only if

b is in the span of Col(A)

Col(A) = Rm if and only if

Ax = b is consistent for ALL b belonging to Rm

dim(Col(A)) =

rank(A)

square matrix of size n x n, Col(A) = Rn if and only if