Key Gas Law Equations to Know for AP Physics 2 (2025)
Gas Laws Overview
Purpose: Describe the relationships between pressure (P), volume (V), temperature (T), and number of moles (n) in gases.
Real-World Applications: Explains phenomena such as weather patterns, breathing mechanics, car engines, and chemical reactions.
Key Assumptions for Ideal Gases:
Gas particles have negligible volume compared to the container.
No interactions (attractions or repulsions) between gas molecules.
Collisions between gas molecules and container walls are perfectly elastic.
Temperature is directly proportional to the average kinetic energy of gas particles.
Key Gas Law Equations
1. Ideal Gas Law :
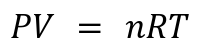
Key Variables:
P: Pressure (in Pascals or atm)
V: Volume (in liters or m³)
n: Number of moles of gas
R: Universal Gas Constant (8.31 J/(mol·K) or 0.0821 L·atm/(mol·K))
T: Temperature (K=°C+273.15)
Description:
Describes the relationship between pressure, volume, temperature, and the amount of gas.
Assumes the gas is "ideal" (no intermolecular forces and negligible molecular size).
Applications:
Calculating missing gas properties (e.g., pressure, volume, etc.).
Understanding behaviors in sealed containers (e.g., inflating balloons).
Example Problem:
A gas occupies 10 L at 2 atm and 300 K. Find the number of moles (n).
Solution:
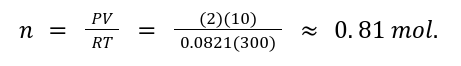
2. Boyle's Law:
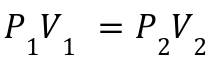
Explanation:
Pressure and volume are inversely proportional if temperature remains constant.
When the volume increases, pressure decreases, and vice versa.
Applications:
Compression and expansion of gases in closed systems.
Scuba diving: Pressure changes as depth increases or decreases.
Key Concept:
Works only at a constant temperature.
Example Problem:
A gas has P1 = 1 atm, V1 = 4L. If compressed to 2 L, what is P2?
Solution:
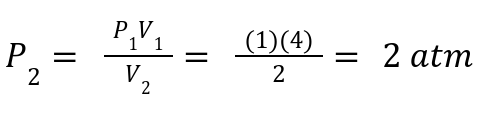
3. Charles's Law:
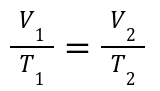
Explanation:
Volume and temperature are directly proportional at constant pressure.
Gas expands when heated and contracts when cooled.
Applications:
Behavior of hot air balloons (hot air expands, increasing volume).
Design of thermal engines and heating systems.
Key Concept:
Temperature must be in Kelvin.
Example Problem:
A gas has V1 = 3L , T1 = 300 K. If heated to 600 K, what is V2?
Solution:
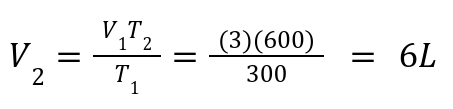
4. Gay-Lussac's Law:
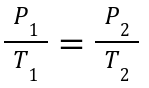
Explanation:
Pressure and temperature are directly proportional at constant volume.
Heating a gas increases its pressure.
Applications:
Pressure cookers: Gas pressure increases as the temperature rises.
Understanding pressurized gas systems (aerosol cans, propane tanks).
Example Problem:
A gas has P1 = 2atm, T1= 300 K .If heated to T2= 450 K, what is P2?
Solution:
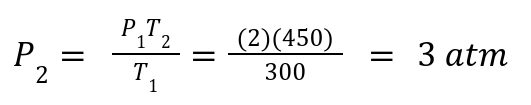
5. Combined Gas Law:
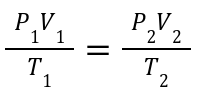
Combines: Boyle’s, Charles’s, and Gay-Lussac’s laws.
Useful When: Pressure, volume, and temperature all change, but the number of moles remains constant.
Applications:
Predicting gas behavior in changing environmental conditions.
Solving problems involving gas systems with multiple variables.
6. Avogadro's Law:
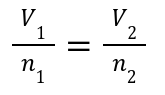
Relationship: Volume is directly proportional to the number of gas moles at constant temperature and pressure.
Doubling the amount of gas (moles) doubles the volume.
Applications:
Stoichiometry in chemical reactions involving gases.
Behavior of gas mixtures in containers.
7. Dalton's Law of Partial Pressures:
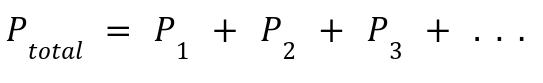
Definition: The total pressure of a gas mixture equals the sum of the partial pressures of each gas.
Pi : Pressure each gas would exert if it alone occupied the container.
Applications:
Explains respiratory processes (e.g., oxygen and carbon dioxide in lungs).
Used in calculating gas behavior in chemical reactions and diving systems.
8. Kinetic Theory of Gases:
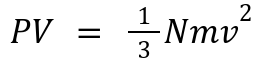
Relates:
P and V: Macroscopic properties.
N, m, and v: Microscopic behavior (number, mass, and velocity of particles).
Key Insight:
Pressure arises from collisions of gas molecules with container walls.
Temperature is proportional to average kinetic energy:
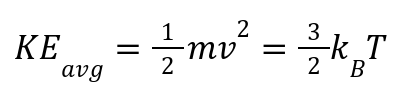
where kB = 1.38 X 10-23 J/K (Boltzmann constant).
Applications:
Explains molecular motion and diffusion rates.
Basis for understanding gas pressure and temperature relationships.
9. Root Mean Square Speed:
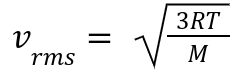
Definition: Calculates the average speed of gas molecules:
R: Gas constant.
T: Temperature in Kelvin.
M: Molar mass (kg/mol).
Key Insight:
Higher temperature → faster molecular motion.
Lighter molecules move faster than heavier ones at the same temperature.
Applications:
Explains gas diffusion and effusion (e.g., Graham's law).
10. Molar Mass from Density:
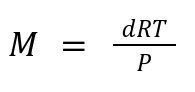
Relates: Gas density (d) to molar mass (M), temperature (T), and pressure (P).
Applications:
Identifying unknown gases based on experimental data.
Calculating molar masses in gas reactions or mixtures.
Applications of Gas Laws in Real Life
Breathing Mechanics:
Boyle’s Law explains how lungs expand (decreasing pressure) to draw in air.
Hot Air Balloons:
Charles’s Law describes the thermal expansion of air as it is heated, increasing volume and causing lift.
Respiration and Gas Mixtures:
Dalton’s Law explains how oxygen and carbon dioxide exchange occurs in the lungs.
Weather Patterns:
Ideal Gas Law explains changes in atmospheric pressure with temperature variations.
Diving and Decompression:
Dalton’s and Henry’s Laws help divers avoid decompression sickness by understanding gas solubility under pressure.
Engines and Combustion:
Combined Gas Law explains the behavior of gases during compression and expansion cycles.