Thermodynamics: It deals with exchange of heat energy between bodies and conversion of heat energy into mechanical energy and vice versa.

Heat: The thermal energy transmitted from one body to another

• Heat is energy in transit.

Temperature: It is measure of an object’s internal energy

The Kinetic Theory of Gases:

• It relates to the macroscopic properties of gases such as pressure, temperature etc.

• Every gas consists of small particles known as molecules.

• The molecules of gas are identical but different than those of another gas.

• The volume of molecules is negligible in comparison to volume of gas.

• The density of gas is constant at all points.

• Consequently, pressure is exerted by gas molecules on the walls of the container.

• No attractive or repulsive exists between the gas molecules.

The Ideal Gas Law:

• It applies to the gases showing ideal behaviour.

• It can’t be applied to real gases.

• The three variables pressure (P), volume (V), temperature (T) are related by the equation:

  PV = nRT

  • Wherein:

    • P = Pressure

    • V = Volume

    • n = Number of Moles of Gas

    • R = Universal Gas Constant (8.314 J/mol.K)

  • It is also written as:

    • P V=N k_{B} T, where k_B is Boltzmann's constant.

• The pressure exerted by N molecules of gas in a container is related to the average kinetic energy. Comparing with the ideal gas law, finally we get the equation:

  K_{\text {avg }}=\frac{3}{2} k_{\mathrm{B}} T

  • Note: Use kelvins as your temperature unit.

• The average kinetic energy =\frac{1}{2}m(v^{2}). After equating:

  • The equation above becomes \frac{1}{2} m\left(v^{2}\right)_{\text {avg }}=\frac{3}{2} k_{\mathrm{B}}

    \sqrt{\left(v^{2}\right)_{\text {avg }}}=\sqrt{\frac{3 k_{\mathrm{B}} T}{m}}

• Root mean square velocity: It gives us a type of average speed that is easy to calculate from the temperature of the gas.

  v_{\mathrm{rms}}=\sqrt{\frac{3 k_{\mathrm{B}} T}{m}}

  Example: In order for the rms velocity of the molecules in a given sample of gas to double, what must happen to the temperature?

  Solution. Temperature is a measure of the average kinetic energy. The velocity is determined from the following equation:

  v_{r m s}=\sqrt{\frac{3 k_{b} T}{m}}

  Since v_{rms} is proportional to the square root of T, the temperature must be quadruple, again, assuming the temperature is given in kelvins.

  Example: A cylindrical container of radius 15cm and height 30 cm contains 0.6 mole of gas at 433 K. How much force does the confined gas exert on the lid of the container?

  Solution. The volume of the cylinder is \pi r²h, where r is the radius and h is the height. Since we know V and T, we can use the Ideal Gas Law to find P. Because pressure is force per unit area, we can find the force on the lid by multiplying the gas pressure times the area of the lid is

  P=\frac{n R T}{V}=\frac{(0.6 \mathrm{~mol})(8.31 \mathrm{~J} / \mathrm{mol} \cdot \mathrm{K})(433 \mathrm{~K})}{\pi(0.15 \mathrm{~m})^{2}(0.30 \mathrm{~m})}=1.018 \times 10^{5} \mathrm{~Pa}

  So, since the area of the lid is \pi r², the force exerted by the confined gas on the lid is:

  F=P A=\left(1.018 \times 10^{5} \mathrm{~Pa}\right) \cdot \pi(0.15 \mathrm{~m})^{2}=7,200 \mathrm{~N}

  This is about 1,600 pounds of force, which seems like a lot. Why doesn’t this pressure pop the lid off? Because, while the bottom of the lid is feeling a pressure (due to the confined gas) iof 1.018 × 10^5 Pa that exerts a force upward, the top of the lid feels a pressure of 1.013 × 10^5Pa (due to the atmosphere) that exerts a force downward. The net force on the lid is

  F_{\text {net }}=(\Delta P) A=\left(0.005 \times 10^{5} \mathrm{~Pa}\right) \cdot \pi(0.15 \mathrm{~m})^{2}=35 \mathrm{~N}

  which is only 8 pounds.

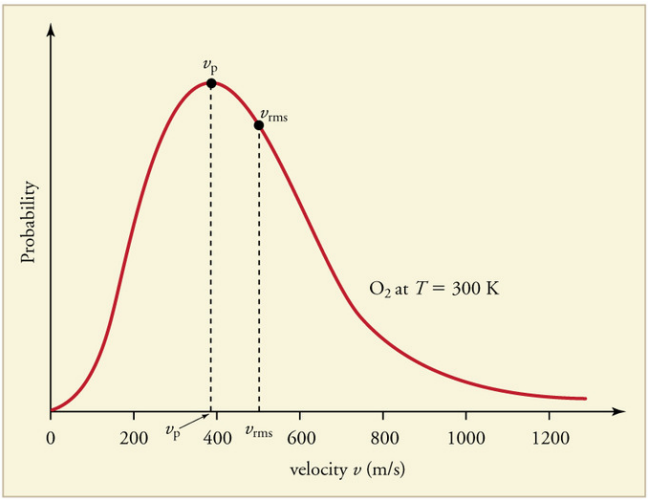
The Maxwell-Boltzmann Distribution:

• The Kinetic theory of gases applies to a large number of particles.

• Some molecules will be moving faster than average and some much slower.

• A graph of the distribution of speeds

The Laws of Thermodynamics:

• Zeroth Law of Thermodynamics: If objects 1 and 2 are in thermal equilibrium with Object 3, then Objects 1 and 2 are in thermal equilibrium with each other.

• First Law of Thermodynamics:

  • It is a special case of the law of conservation of energy that describes processes in which only internal energy changes and the only energy transfers are by heat and work.

    \Delta U=Q+W

  • It can be used to calculate the work done.

    (W=-P \Delta V)

• Thermodynamic Processes:

  • Isothermal: Temperature remains constant.

  • Adiabatic: No transfer of heat.

  • Isobaric: Pressure remains constant.

  • Isochoric: Volume remains constant.

• Second Law of Thermodynamics:

  • It describes how systems evolve over time.

  • Entropy describes it all.

    • It is associated with a state of randomness, disorder, or uncertainty.

    • The total entropy of the system and its surroundings increased.

    • Heat always flows from an object at higher temperature to an object at lower temperature, never the other way around.

  Example: What’s the value of W for the process ab following path 1 and for the same process following path 2 (from a to d to b), shown in the P–V diagram below?

  

  Solution.

  Path 1. Since, in path 1, P remains constant, the work done is just -P \Delta V:

  \begin{gathered} W=-P \Delta V=-\left(1.5 \times 10^{5} \mathrm{~Pa}\right)\left[\left(30 \times 10^{-3} \mathrm{~m}^{3}\right)-\left(10 \times 10^{-3}\right.\right. \\\left.\left.\mathrm{m}^{3}\right)\right]=-3,000 \mathrm{~J}\end{gathered}

  Path 2. If the gas is brought from state a to state b, along path 2, then work is done only along the part from a to d. From d to b, the volume of the gas does not change, so no work can be performed. The area under the graph from a to d is

  \begin{aligned} W=-\frac{1}{2} h\left(b_{1}+b_{2}\right) & =-\frac{1}{2}(\Delta V)\left(P_{a}+P_{d}\right) \\ & =-\frac{1}{2}\left(20 \times 10^{-3} \mathrm{~m}^{3}\right)\left[\left(1.5 \times 10^{5} \mathrm{~Pa}\right)+\left(0.7 \times 10^{5} \mathrm{~Pa}\right)\right] \\& =-2,200 \mathrm{~J} \end{aligned}

Heat Engines:

• It is a device which uses heat to produce useful work.

• For any cyclic heat engine, some exhaust heat is always produced. It’s impossible to completely convert heat into useful work.

• Working: Energy in form of heat comes into the engine from a high temp source, some of this energy is converted in to useful work, the remains are ejected as exhaust heat. Then, the cycle returns to original state and the cycle resumes again.

  Example: A heat engine draws 800 J of heat from its high-temperature source and discards 450 J of exhaust heat into its cold-temperature reservoir during each cycle. How much work does this engine perform per cycle?

  Solution. The absolute value of the work output per cycle is equal to the difference between the heat energy drawn in and the heat energy discarded:

  |W|=Q_{\mathrm{H}}-\left|Q_{\mathrm{C}}\right|=800 \mathrm{~J}-450 \mathrm{~J}=350 \mathrm{~J}

Heat Transfer:

• There are three ways in which the heat is transferred:

  • Conduction

  • Convection

  • Radiation

Conduction:

• Radiation Heat conducts from one point to another only if there is a temperature difference between the two objects.

• The rate at which heat is transferred is given by:

  \frac{Q}{\Delta t}=\frac{k A \Delta T}{L}

Convection: The movement caused within a fluid by the tendency of hotter and therefore less dense material to rise, and colder, denser material to sink under the influence of gravity, which consequently results in transfer of heat.

Radiation:

• Emission or transmission of energy in the form of waves or particles through space or through a material medium.