Fluids

• The substances that can flow. This property generally applies to liquids and gases. We can't tell that solids can flow due to their high interatomic forces of attraction.

Density

• The mass per unit volume of a substance is defined as density. Density is a positive scalar quantity.

• So, density at a point of a fluid is expressed as:

• p= m/V

• S.l unit: kg/m³

• C.G.S unit: g/cc

• Example: if 10-3 m3 of oil has a mass of 0.8 kg, then the density of this oil is:

• Solution: p = m/v = 0.8/10^-3 = 800 kg/m³

Pressure

• Pressure P is defined as the magnitude of the normal force acting per unit surface area.

• S.I unit: Pascal (Pa); 1Pa = 1 N/m²

• Practical units: atmospheric pressure (atm), bar, torr

• 1 atm = 1.01325 × 10^5 Pa = 1.01325 bar = 760 torr = 760 mm of Hg

• Example: A vertical column made of cement has a base area of 0.5 m2. If its height is 2 m, and the density of cement is 3000 kg/m3, how much pressure does this column exert on the ground?

• Solution: The force the column exerts on the ground is equal to its weight, mg, so we’ll find the pressure it exerts by dividing this by the base area, A. The mass of the column is equal to pV, which we calculate as follows:

• m = pV =pAh = (3 × 10³ kg/m³) (0.5m²) (2m) = 3 × 10³kg

• Therefore, P = F/A = mg/A = (3 × 10³kg)(10 N/kg) / 0.5m² = 6 × 10^4 Pa = 60 kPa

Hydrostatic Pressure

• It is the pressure due to liquid.

• It depends only on the density of the liquid and the depth below the surface.

• Pliquid = force/area = Fg liquid / A = p(lwh)g /lw =pgh

• Total (absolute) pressure: Ptotal = P0 + Pliquid = P0 + PGH

• Ptotal = Patm + pgh

• Note: the total pressure comes into account when the tank were open to the atmosphere.

Buoyancy

• If a body is fully or partially immersed in a fluid, it experiences an upward force due to the fluid called buoyant force, and the phenomenon is called buoyancy.

• It uses Archimedes principle.

• Buoyant force: Fbuoy= Pfluid V sub g

• Vsub/ V = Pobject/Pfluid

• Example: An object with a mass of 150 kg and a volume of 0.75 m3 is floating in ethyl alcohol, whose density is 800 kg/m3. What fraction of the object's volume is above the surface of the fluid?

• Solution: The density of the object is Pobject = m/V = 150kg/0.75m³ = 200kg/m³

• The ratio of the object density to the fluid’s density is Pobject/ Pfluid = 200kg/m³ /800kg/m³ = ¼

• This means that ¼ of the object’s volume is below the surface of the fluid; therefore, the fraction above the surface is 1-(1/4) =3/4.

• Make sure you know exactly what the question is asking.

• Typically you can use this equation to find the volume submerged, but this question asks for the volume not submerged.

  Buoyancy diagrams

• Diagram showing an object floating in a liquid.

• Diagram showing an object with a density greater than the fluid density as it sinks to the bottom of the tank.

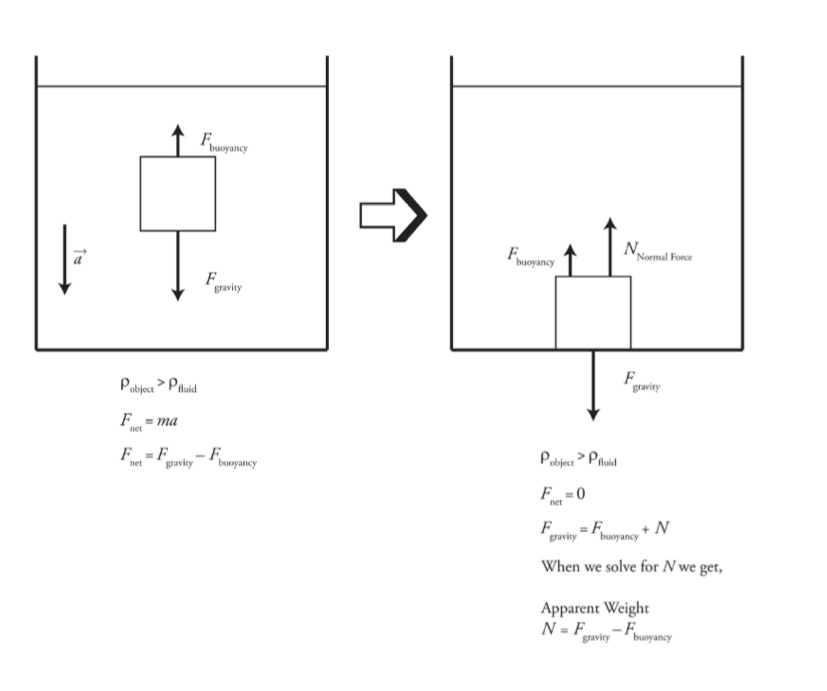
The Continuity Equation: Flow Rate and Conservation of Mass

The Volume Flow Rate

• It is the volume of fluid that passes through a particular point per unit of time.
  volume flow rate: f = Av

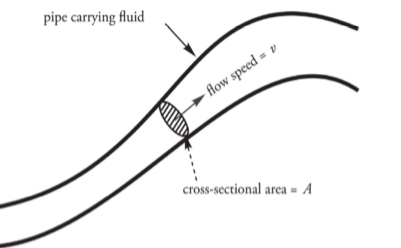
• S.I unit: m^3/s

The Continuity Equation:

• The density of the fluid is constant.

• A1V1 =A2V2

• Example: A circular pipe of non-uniform diameter carries water.
  At one point in the pipe, the radius is 2 cm and the flow speed is 6m/s.

  • What is the volume flow rate?

  • What is the flow speed at a point where the pipe constricts to a radius of 1 cm?

• Solution

  • At any point, the volume flow rate, f, is equal to the cross-sectional area of the pipe multiplied by the flow speed.

    

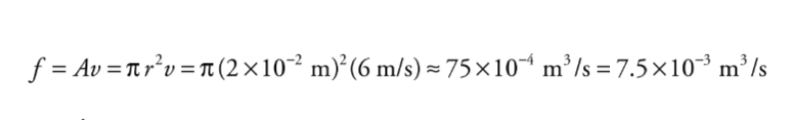
  • By the Continuity Equation, we know that the volume flow rate must be the same at all points, so the volume flow rate must be the same as in part a.

    
    

  • A second approach to part (b) is to use proportional reasoning. From the Continuity Equation, we know that v, the flow speed, is inversely proportional to A, the cross-sectional area of the pipe.

  • If the pipe radius decreases by a factor of 2 (from 2cm to 1cm), then A decreases by a factor of 4, because A is proportional to r^2.

  • If A decreases by a factor of four then v will increase by a factor of 4, Therefore, the flow speed at a point where the

    pipe's radius is 1 cm will be 4 • (6 m/s) = 24 m/s.

Bernoulli's Equation: Conservation of Energy in Fluids

• The fluid is incompressible.

• The fluid's viscosity is negligible.

• The fluid is streamlined.

• The equation looks very similar to the conservation of energy with total mechanical energy.

• An alternative is a way of stating Bernoulli's equation

• P + pgy + ½ pv²

• A1, A2: Cross-sectional areas at points 1 and 2

• p1, p2: Pressures

• v1, v2 : Velocities

• h1, h2, : Elevations

• Example: In the figure below, a pump forces water at a constant flow rate through a pipe whose cross-sectional area, A, gradually decreases: at the exit point, A has decreased to ⅓

  its value at the beginning of the pipe. If y = 60 cm and the flow speed of the water just after it leaves the pump (Point 1 in the figure) is 1m/s, what is the gauge pressure at Point 1?

• Solution: We will apply Bernoullis equation to point 1 and the exit point, point 2. We will choose the level of point 1 as the horizontal reference level; this makes y1 = 0. Now, because the cross-sectional area of the pipe decreases by a factor of 3 between points 1 and 2, the flow speed must increase by a factor of 3, that is v2= 3V1. Since the pressure at 2 is Patm Bernoulli’s equation becomes:

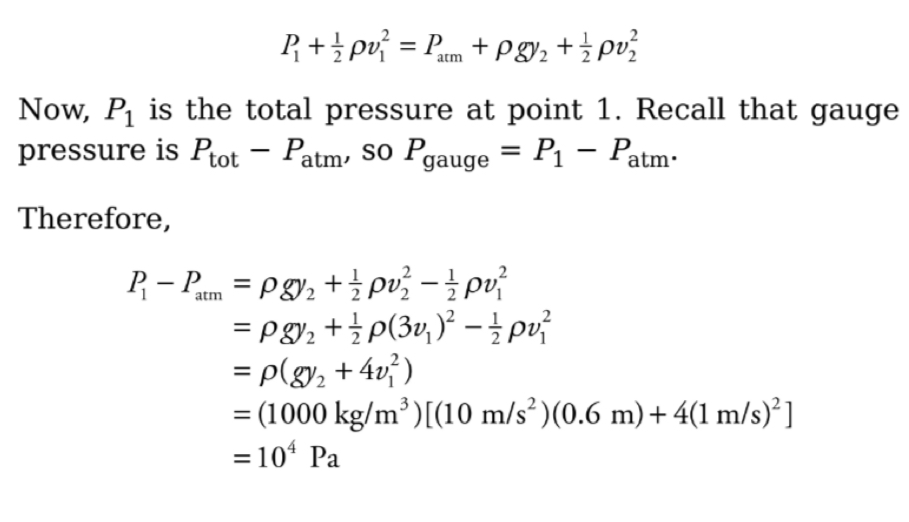
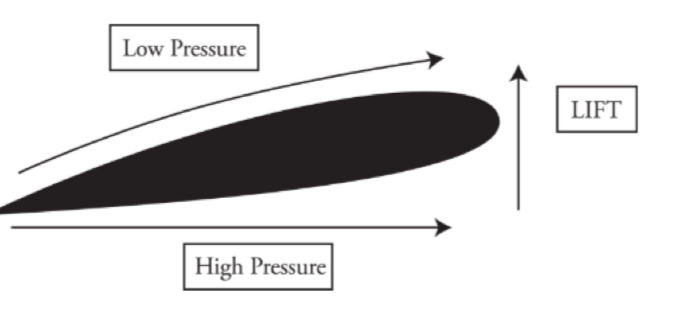
Bernoulli's Effect

• At comparable heights, the pressure is lower where the flow speed is greater.
  

• p1 + ½ pv1² = p2 + ½ pv2²

Air flow

• The air on the bottom has greater pressure and pushes up on the wing giving the airplane lift force.