Probability - Quiz 3

conditional probability

the probability of event A occurring given event B has already occurred

picture

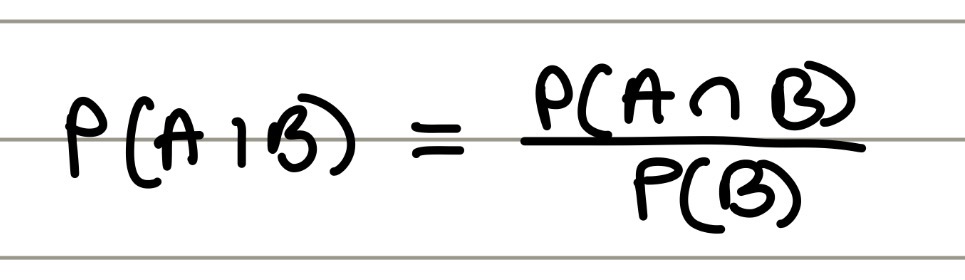
independence

• event A occurring has nothing to do with event B occurring

  • information about A is irrelevant to the probability of B (and vice versa)

• equations

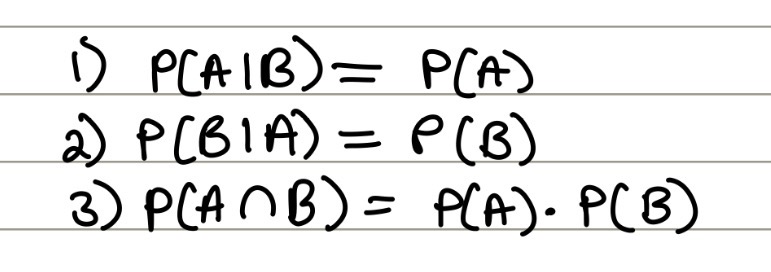
independence equations

• at least one of these equations need to be true:

  1. P(A | B) = P(A)

  2. P(B | A) = P(B)

  3. P(A ⋂ B) = P(A) * P(B)

mutually exclusive

• event A and event b cannot happen at the same time

• form of dependence

• A ⋂ B = ∅

independence ≠ mutual exclusivity

• if A and B are mutually exclusive, P(A | B) = 0

• if P(A) ≠ 0, then P(A) ≠ P(A | B)

  • A and B are not independent

Additive Law

• probability of a union of 2 events

• P(A ⋃ B) = P(A) + P(B) - P(A ⋂ B)

  • ME: P(A ⋂ B) = 0

• Ex: A = B, then (A ⋃ B) = A, (A ⋂ B) = A

Multiplicative Law

• probability of an intersection of 2 events

  • definition of conditional probability flipped around

• independent events

  • P(A ⋂ B) = P(A) * P(B)

Multiplicative Law Probability Statement

P(A ⋂ B) = P(A | B) * P(B)

Multiplicative Law Probability Statement

P(B ⋂ A) = P(B | A) * P(A)