Quantum phenomena

Bohr’s postulates

• electrons are confined to circular orbits around a nucleus. We consider 1 electron orbiting the nucleus

• the nucleus can posses any number of nucleons

• electrons have an angular momentum L, that is an integer number of h-bar

• an electron moves in non-radiating circular orbits called stationary states (classical predicts electrons should radiate energy and spiral towards the nucleus)

• an electromagnetic wave will be emitted when an electron changes orbitals

What is the periodic boundary condition?

• the circumference of an electron’s orbit must be an integer number of de Broglie wavelengths

2\pi r=n\lambda which can be rearranged to:

mvr=L=n\hbar where L is angular momentum.

What is meant by the principle quantum number?

The energy level an electron occupies in an atom. Represented by n, a positive integer.

What is meant by quantisation?

When a variable can only assume discrete values.

Equation for Bohr radius

r=\frac{1}{k}\frac{n^2\hbar^2}{\mu Ze^2}

Equation for Bohr velocity

v=\frac{n\hbar}{\mu r}=k\frac{Ze^2}{n\hbar}

Equation for Bohr energy (levels)

E_{n}=\frac{\mu Z^2e^4}{2\hbar^2n^2}\cdot k^2=-13.6\frac{Z^2}{n^2}

What are two experiments that provide evidence for electrons occupying specific orbital energies

• Frank-Hertz experiment

• Electron emission spectra

What is the Rydberg-Ritz formula

\frac{1}{\lambda}=\frac{13.6Z^2}{hc}\left(\frac{1}{n_{f^{}}^2}-\frac{1}{n_{i}^2}\right)=R\left(\frac{1}{n_{f}^2}-\frac{1}{n_{i}^2}\right)

Where nf is the final energy level and ni is the intial energy level

What is the Rydberg-Ritz formula used for

To predict wavelengths of emitted photons in atomic emission spectra. Predicts wavelengths for different energy level transitions.

What is the Rydberg constant

R=\frac{13.6Z^2}{hc}

For Bohr energy levels/two particles orbiting one another, which mass is used?

The reduced mass.

\mu=\frac{m_1m_2}{m_1+m_2}

Bohr model of the atom

• electron moves in circular orbits under the influence of the attractive Coulomb force, F.

• Proton mass » electron mass, so the proton is stationary.

What are the flaw’s of Bohr’s semi-classical approach?

• Fine structure splitting observed in the Balmer spectrum (lines are doublets due to electron spin which Bohr didn’t account for)

• Electrons orbiting in well-defined orbits \Delta r=0 violates the Uncertainty Principle \Delta p\Delta r\ge\frac{\hbar}{2}

• No fundamental justification for stationary states

• The semi-classical approach fails more complex atoms

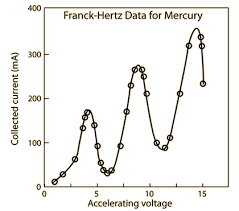
Explain the Franck-Hertz experiment

• Electrons accelerated, using adjustable accelerating voltage V, between cathode and anode

• They accelerate through a gas (neon/mercury vapour)

• The current is recorded for different V and I-V graph is plotted.

• Graph has multiple peaks and dips

• Peaks in I are observed whenever \Delta V changes by difference between energy levels.

• Below \Delta V, electrons collide elastically, above they collide inelastically resulting in excitation.

Explain electron emission spectra experiment

• gas inside a discharge tube has a voltage applied to it and gas excites

• As gas then de-excites, photons of discrete wavelengths are emitted

• Emitted photons pass through a diffraction grating and when projected onto a screen, only discrete wavelengths can be observed on the screen

• Wavelengths correspond to energies of the photons, therefore electron energy levels in an atom

Which experiments can be used to demonstrate particle-like behaviour of EM radiation

• the photoelectric effect - Millikan experiment

• Compton scattering

Which experiments can be used to demonstrate wave behaviour of particles (electrons)?

• Electron diffraction: Davisson-Germer experiment

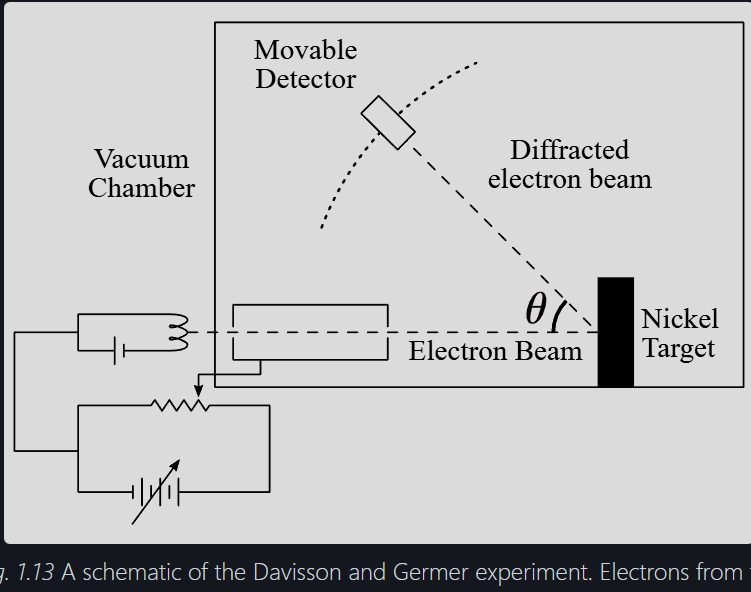
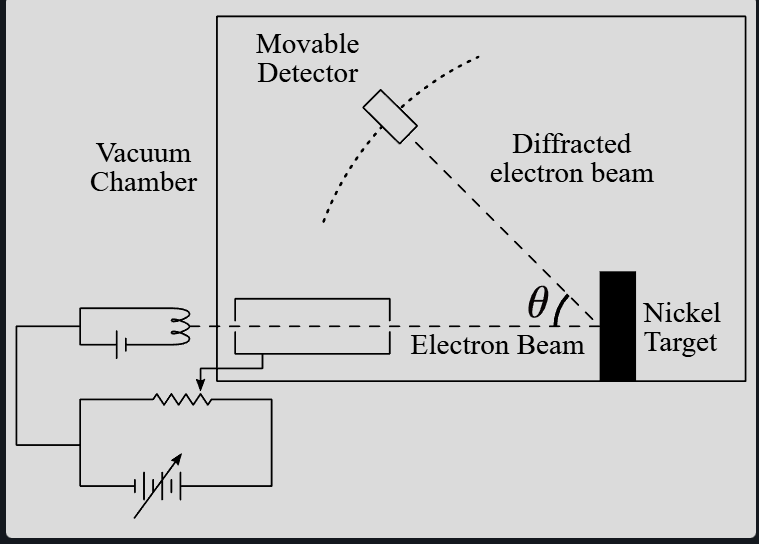
Explain the Davisson-Germer experiment

• electrons accelerated through a potential difference at a nickel crystal target (inside a vacuum)

• A moveable detector records the current at varying angles

• Electron current (intensity) is recorded for each detector angle

• For V = 54eV, angle = 50

• at certain angles, the detector current shows maxima, indicating constructive interference. This is a wave behaviour.

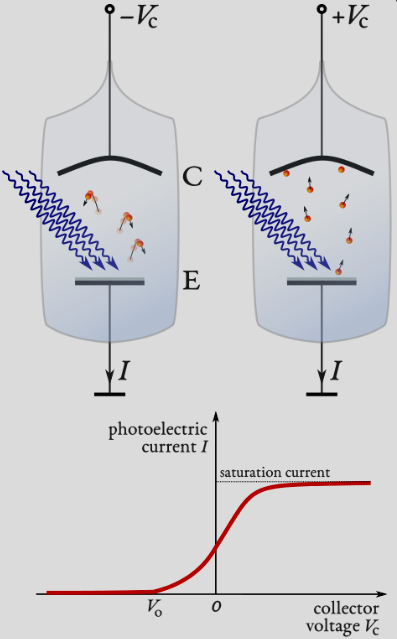
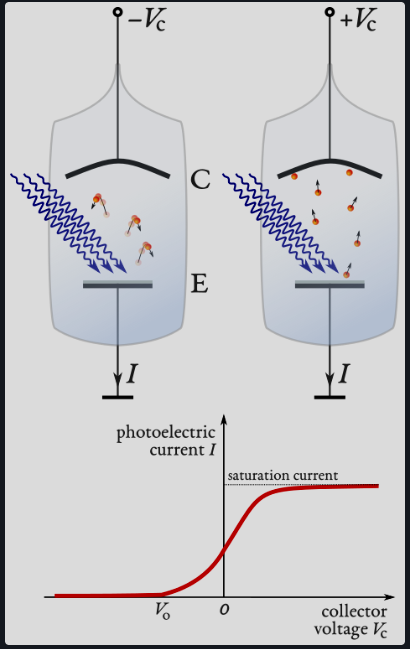
Explain the Millikan experiment

• Glass vessel with anode of work function and cathode in series with power supply and ammeter.

• Light is incident on the anode, photoelectrons are emitted and accelerated by the potential difference between anode and cathode

• Photoelectrons incident on the cathode result in a current recorded by the ammeter.

• Anode is at a negative bias such that only electrons with sufficient EK to overcome repulsion are attracted.

• Voltage between cathode and anode is increased until current = 0, this is the stopping potential.

• Varying intensity does not change the stopping potential, but varying frequency does - opposing classical predictions

• Einstein said if EM waves behaved as particles where E=hf the result is valid.

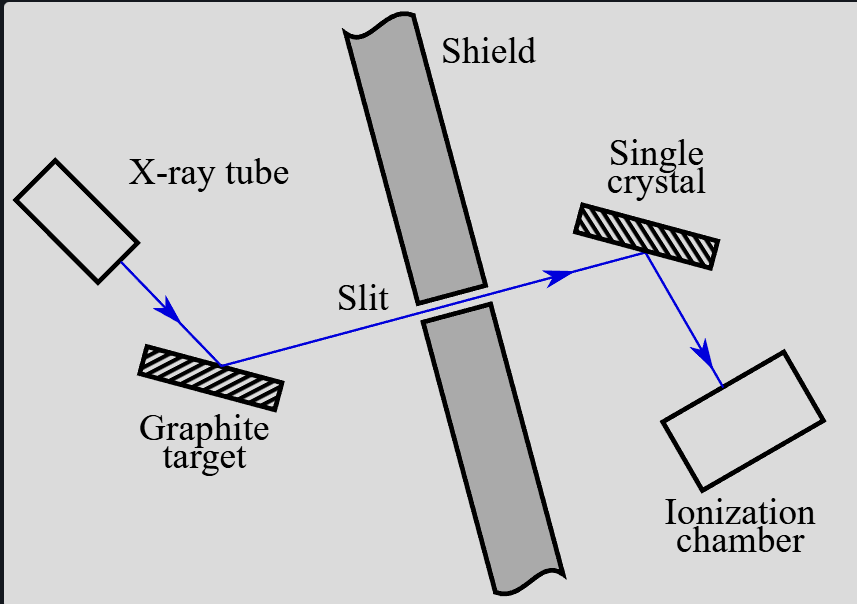
Explain compton scattering

Compton suggested

• if photons were incident on loosely bound electrons in an atom, the electrons would recoil

• the electrons would therefore absorb energy, reducing the photon’s energy (and increasing its wavelength)

• Linear momentum between the photon and electron is conserved

• Graph intensity against wavelength for different scattering angles. 2 peaks observed, indicating a change in wavelength therefore energy for scattered photon

• Carbon used due to its loosely bound electrons.

Compton scattering formula

\lambda^{\prime}-\lambda=\frac{h}{mc}\left(1-\cos\left(\theta\right)\right)

Where \theta is the scattering angle for the incident photon and \lambda^{\prime} is the wavelength of scattered light.

What are the results of the Millikan experiment?

• stopping potential is plotted against frequency of incident light (for a single metal)

• x-intercept is the threshold frequency

• y-intercept is the work function

• Planck’s constant can be determined V_0=\frac{h}{q}f-\frac{\phi}{q} where q is electron charge.

What are the applications of the photoelectric effect?

• Solar cells: Solar cell electrons are excited across the band gap of the semiconductor into the conduction band, generating electricity

Left to do:

• derive compton scattering formula

• electron diffraction theory

What is meant by the reduced mass

an effective mass used to account for the fact that both the electron and the nucleus orbit their common centre of mass, rather than the electron orbiting a stationary nucleus.

When is m vs reduced mass used?

Reduced mass:

• Bohr energy levels/radisu/rydberg constant/schrodinger/spectral lines

So anytime the entire atom is invovled.