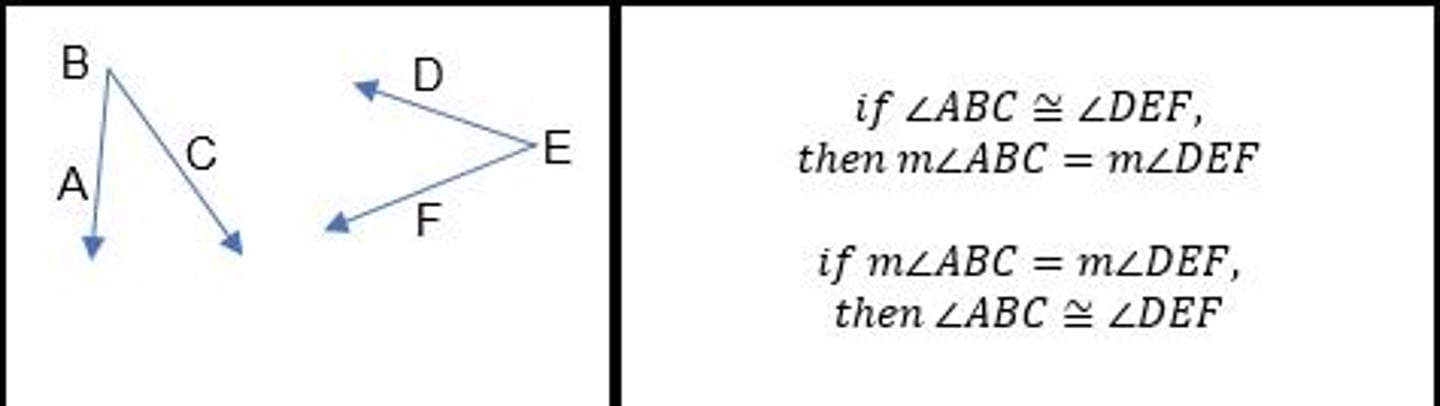Basic Geometry Properties Postulates and Theorems Ch 2 Part 1

Through any two points,

there is exactly one line (postulate)

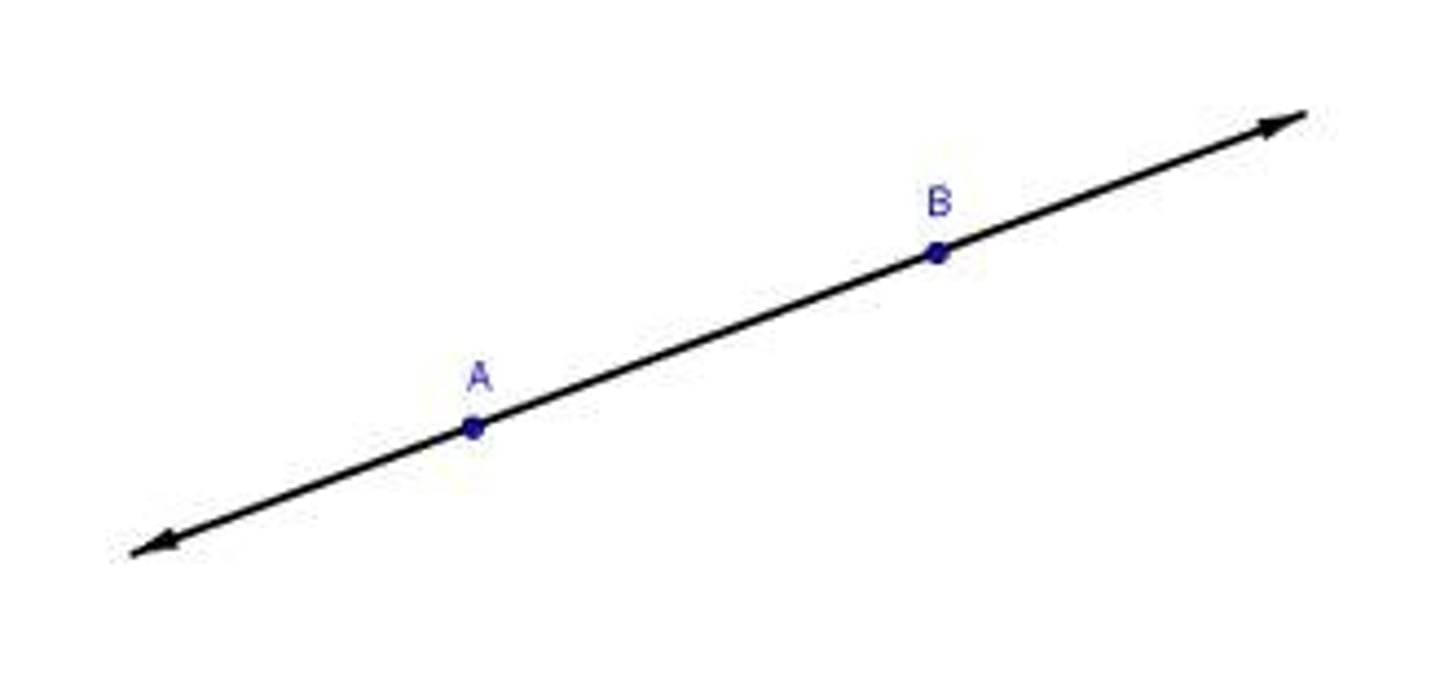
Through any three noncollinear points,

there is exactly one plane (postulate)

A line contains

at least two points (postulate)

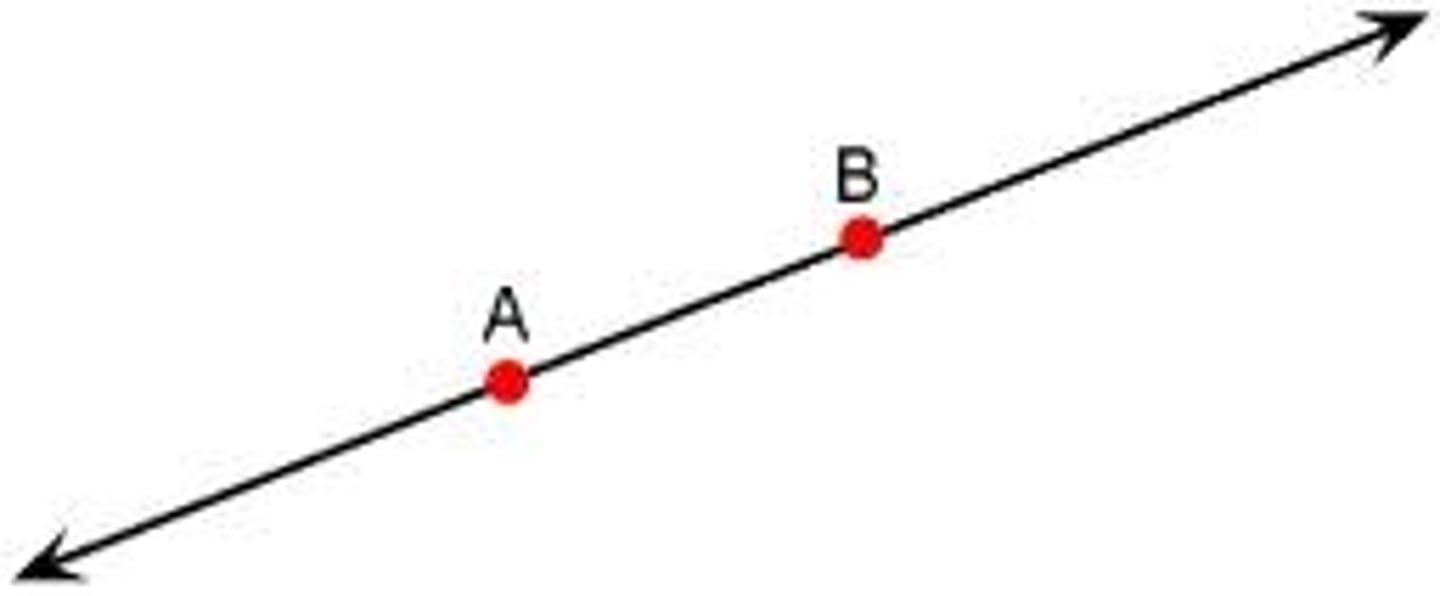
A plane contains

at least three noncollinear points (postulate)

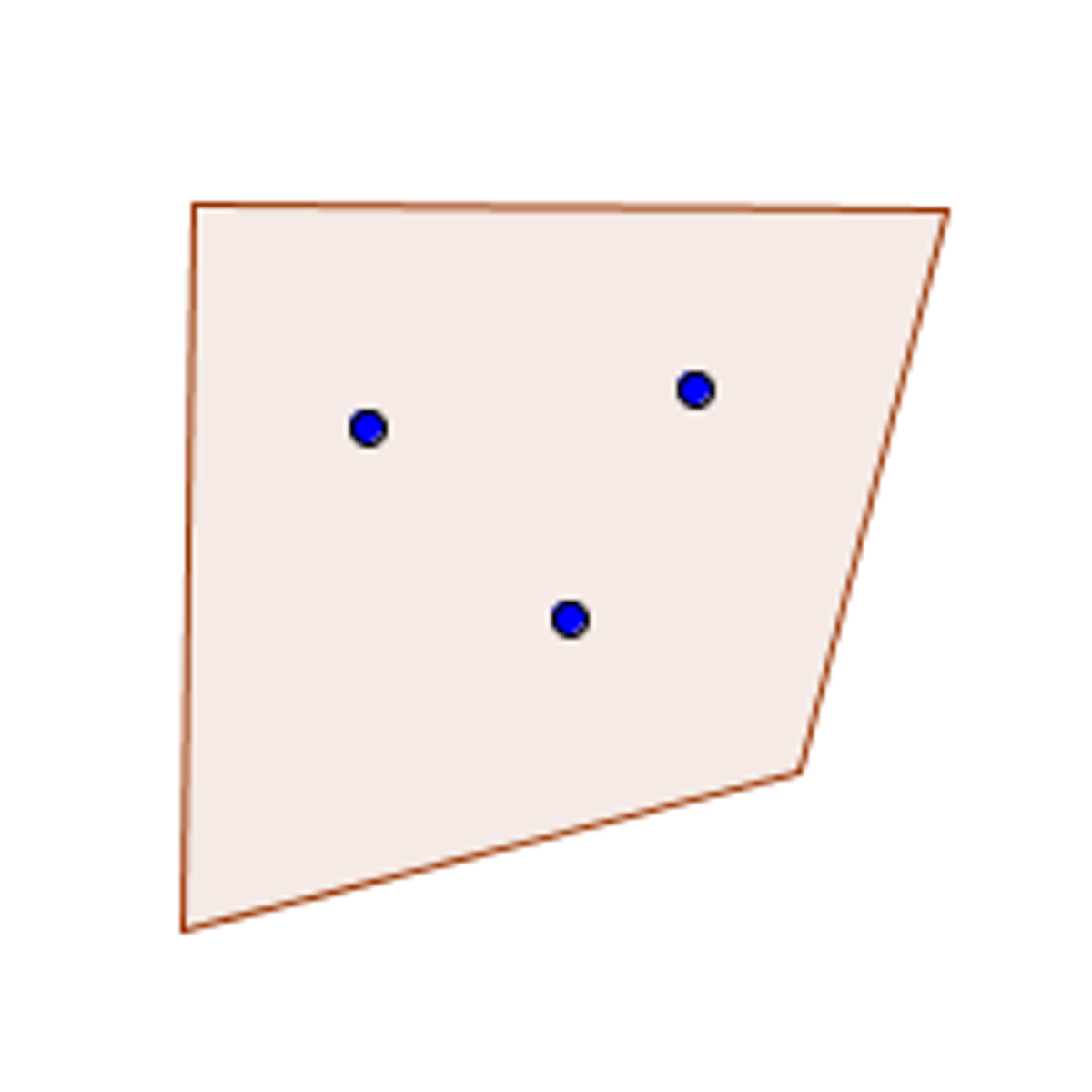
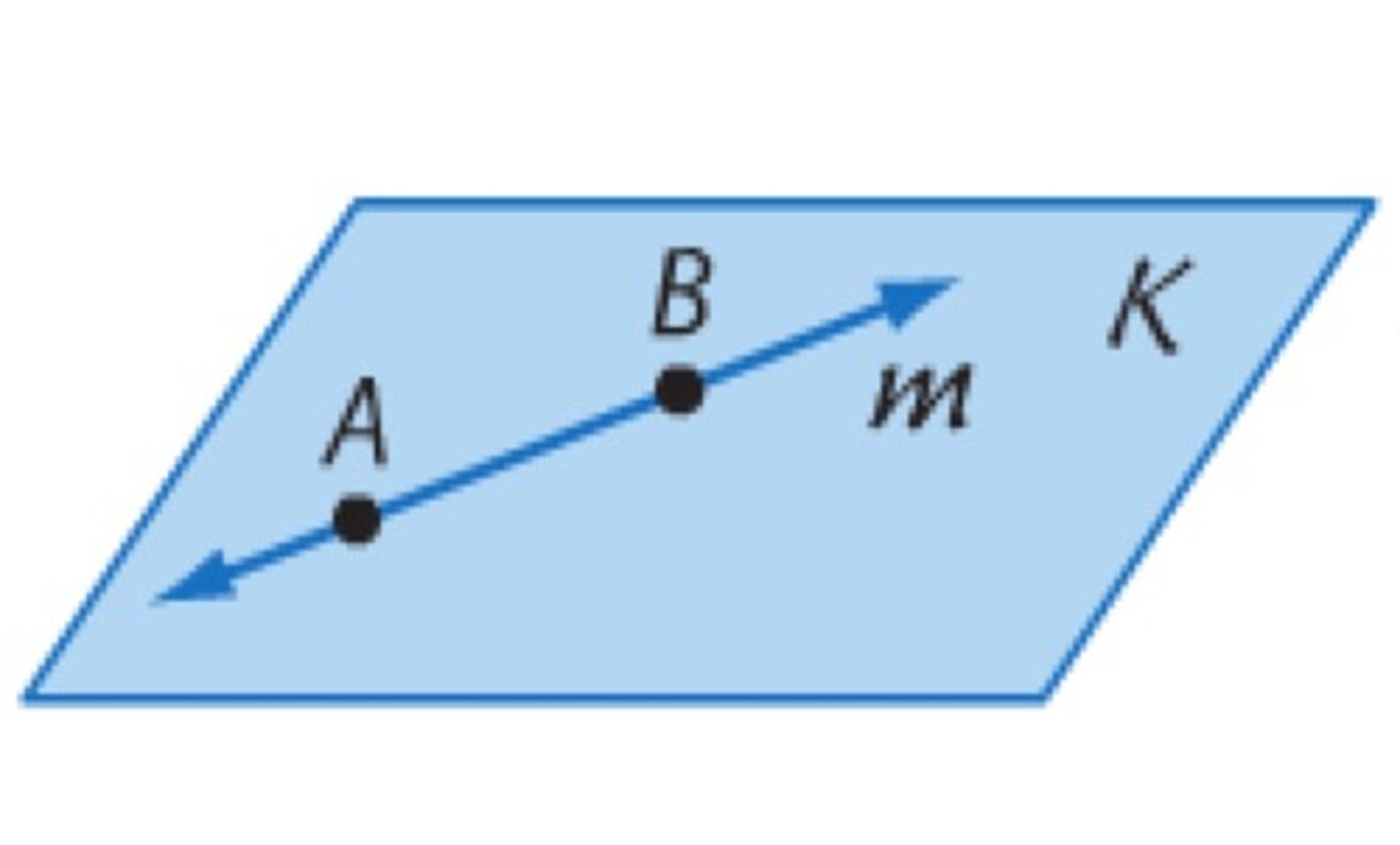
If two points lie in a plane,

then the entire line containing those points lies in that plane (postulate)

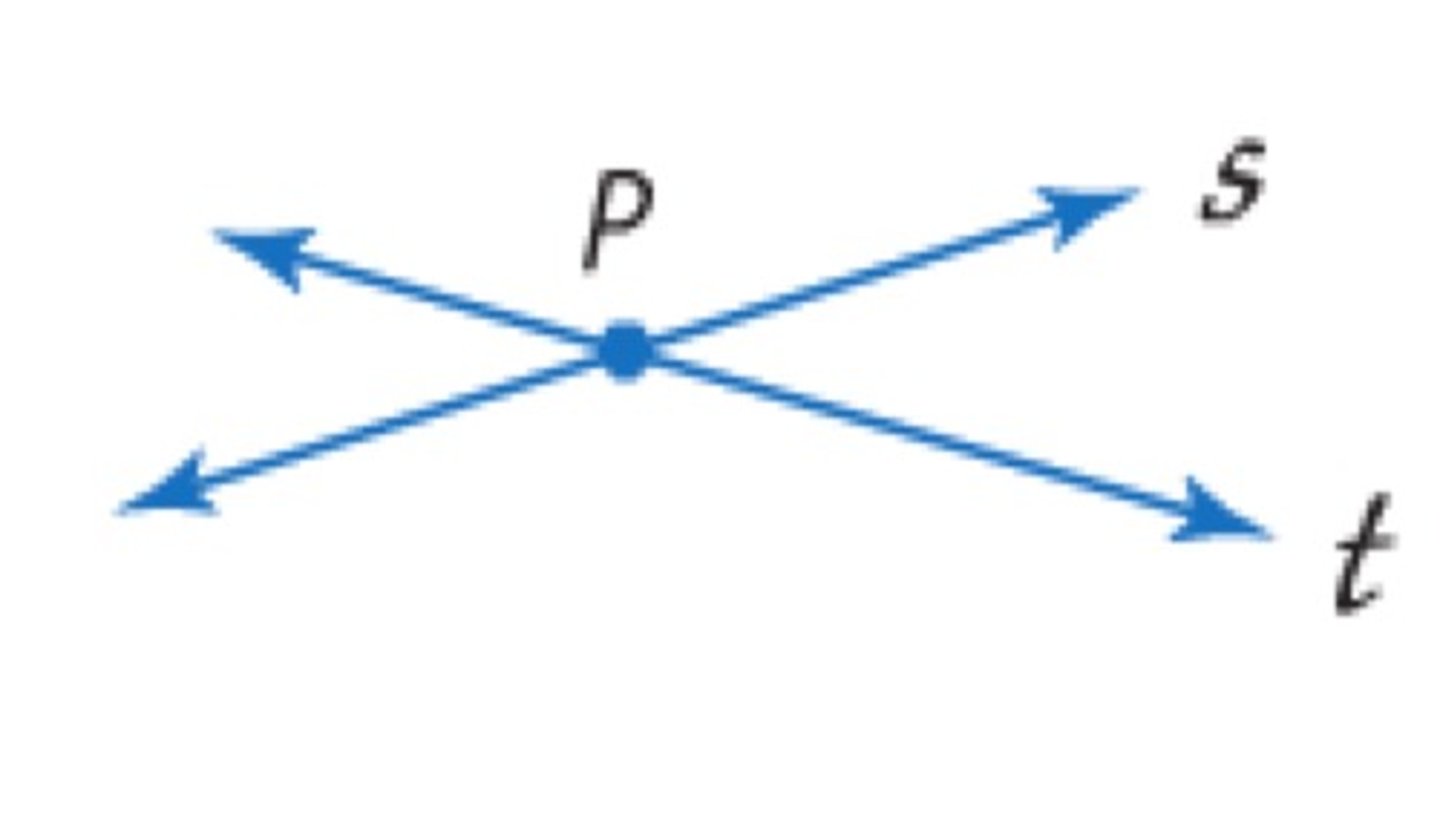
If two lines intersect,

then their intersection is exactly one point (postulate)

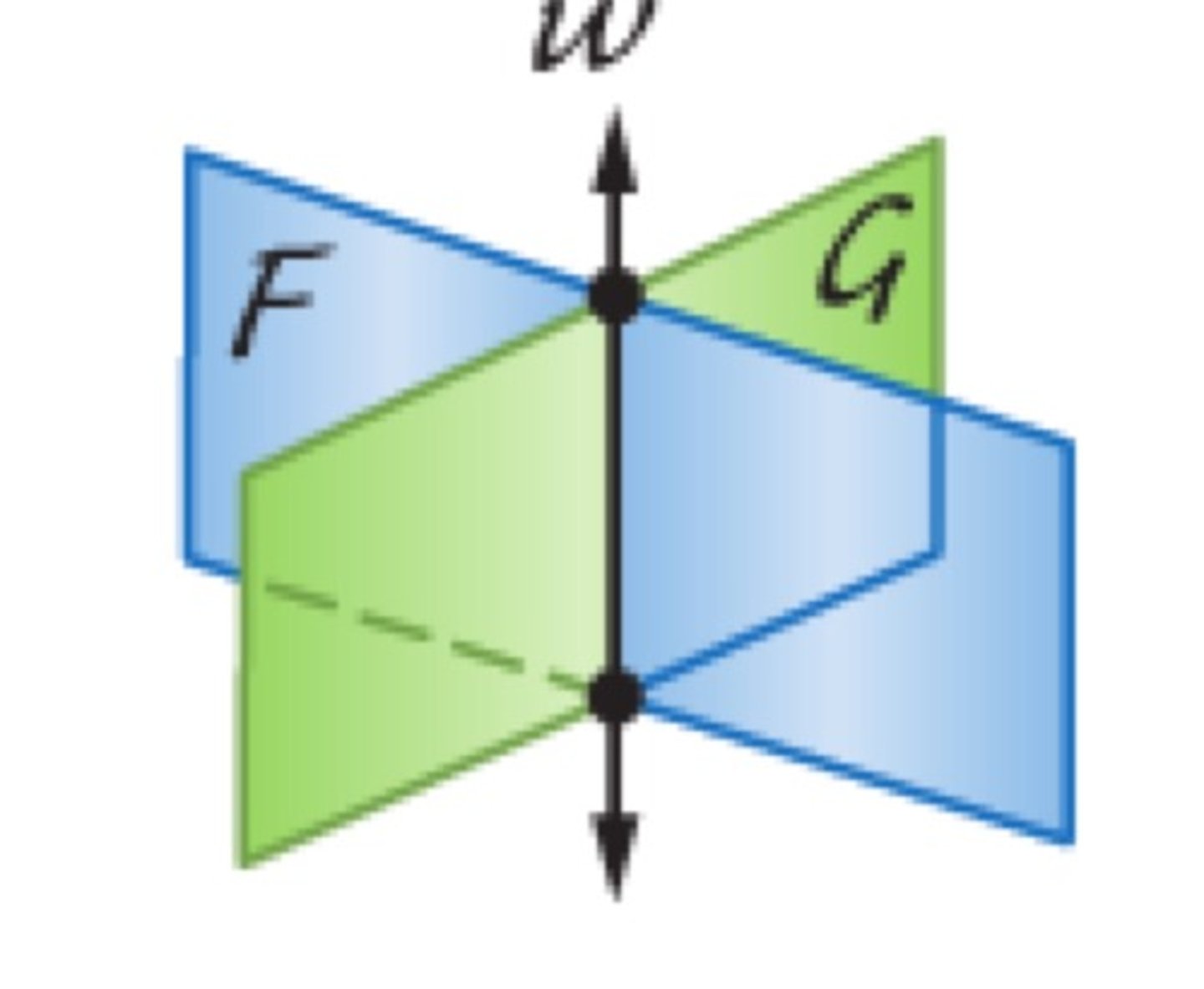
If two planes intersect,

then their intersection is a line (postulate)

Midpoint Theorem

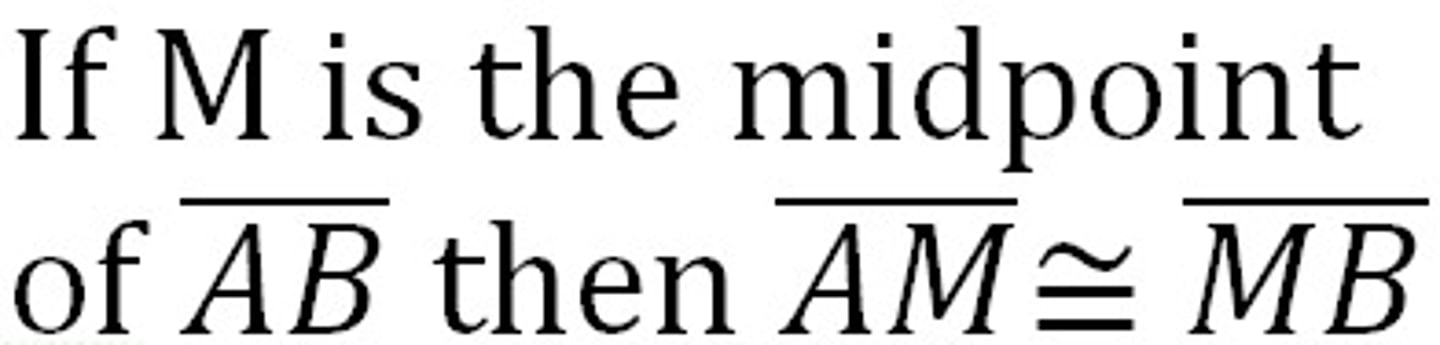
Segment Addition Postulate

If B is between A and C, then AB +BC=AC.

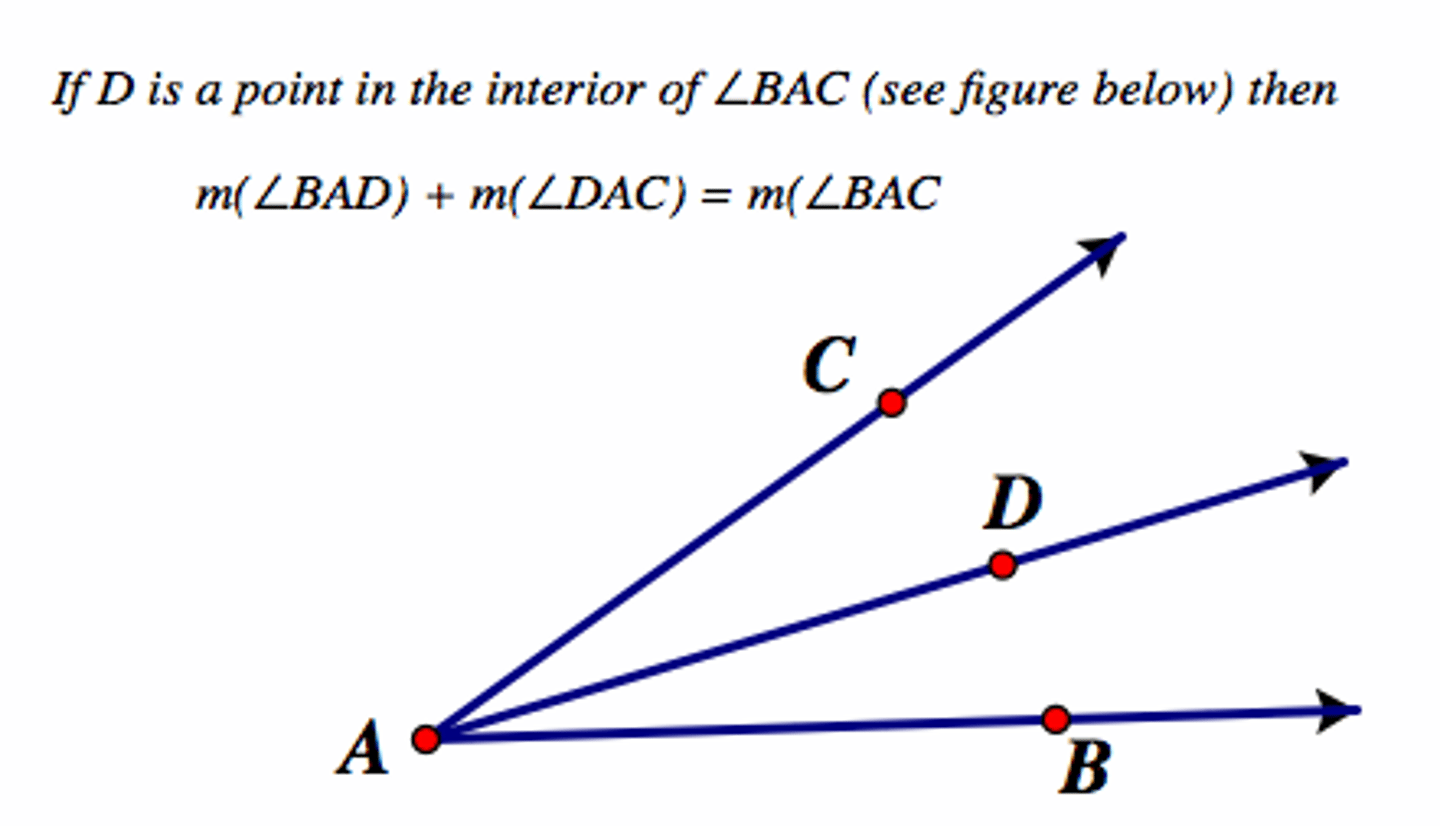
Angle Addition Postulate

D is in the interior of ∠ABC if and only if m∠ABD + m∠DBC = m∠ABC

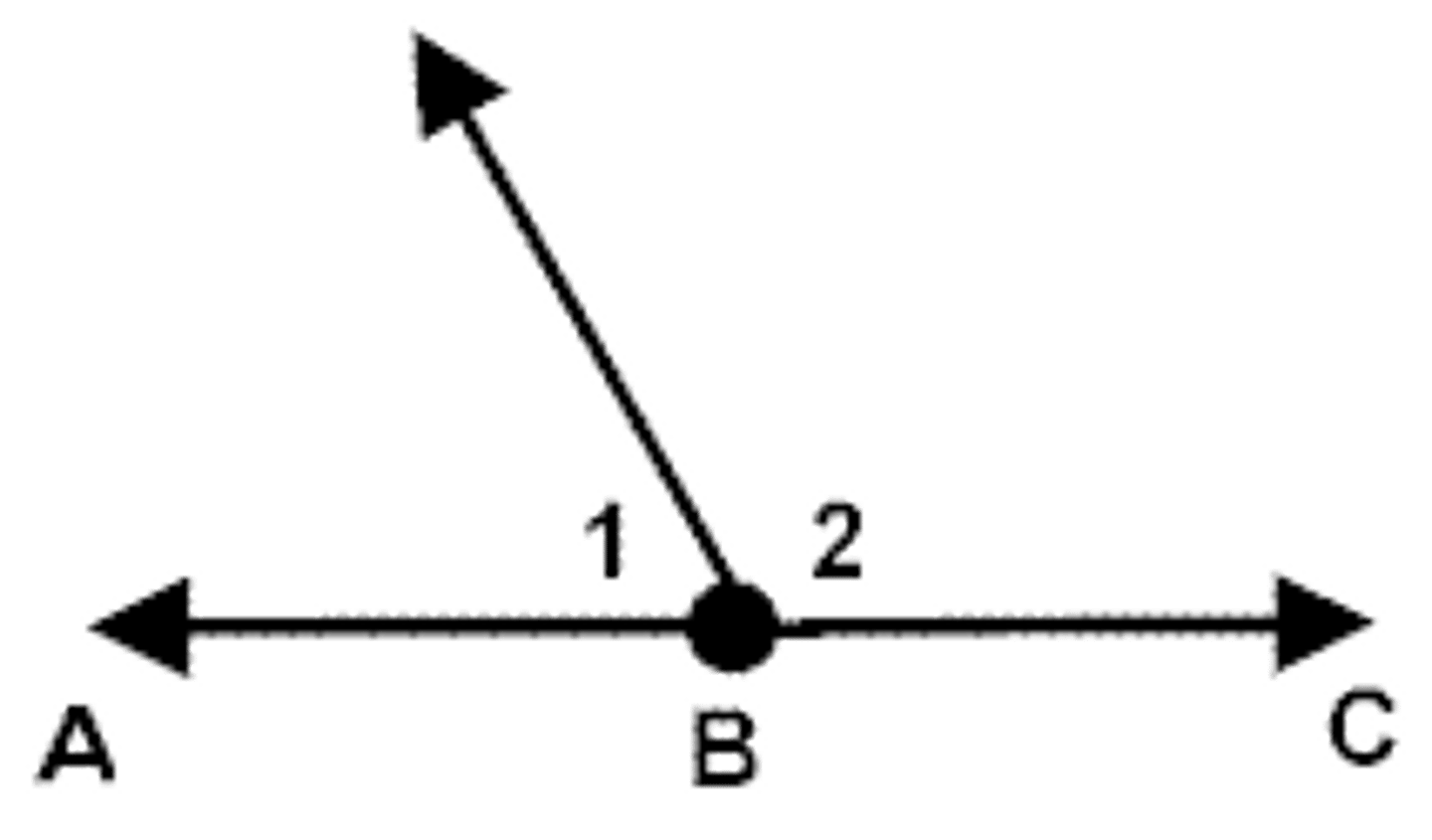
Supplement Theorem

If two angles form a linear pair, then they are supplementary angles.

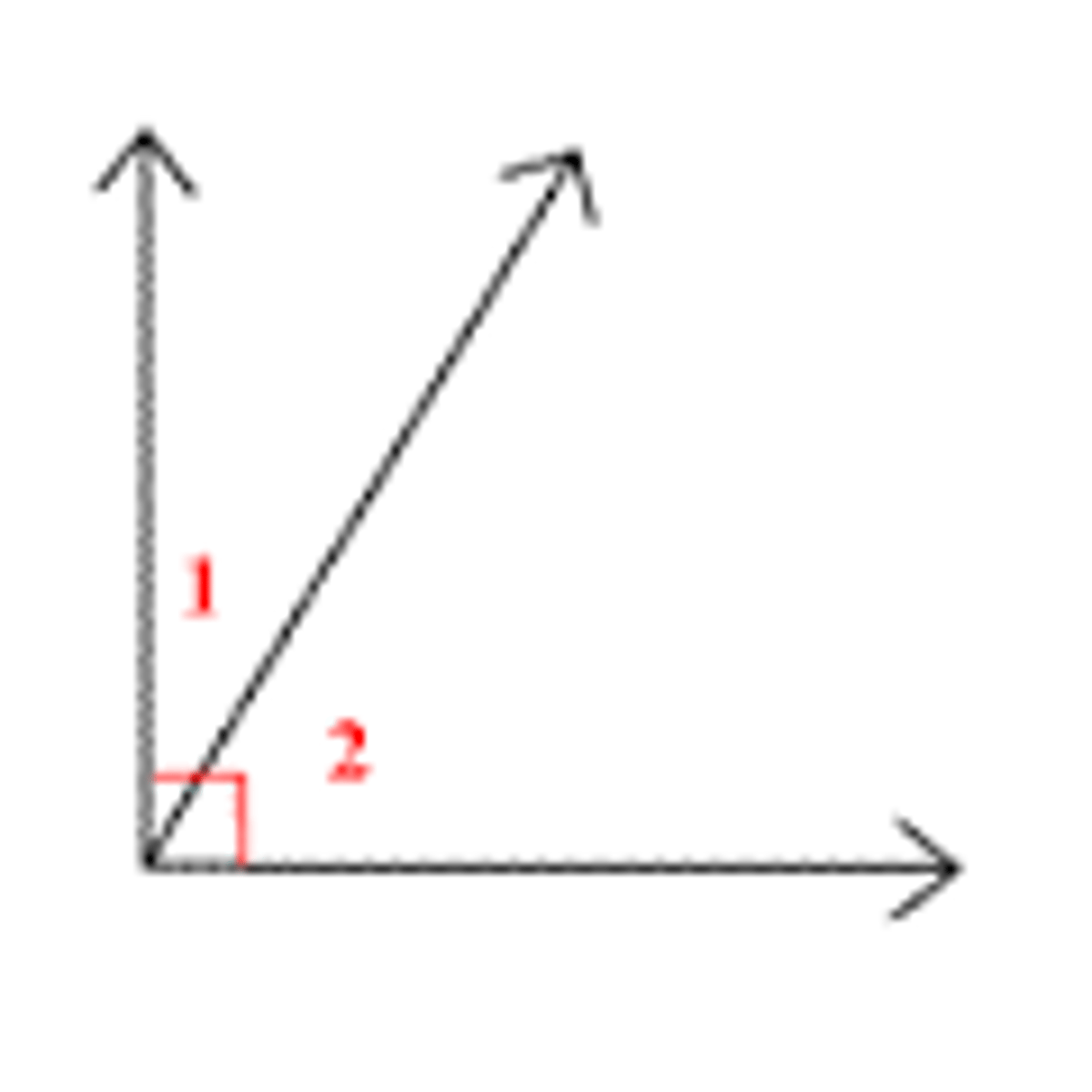
Complement Theorem

If the noncommon sides of two adjacent angles form a right angle, then the angles are complementary angles.

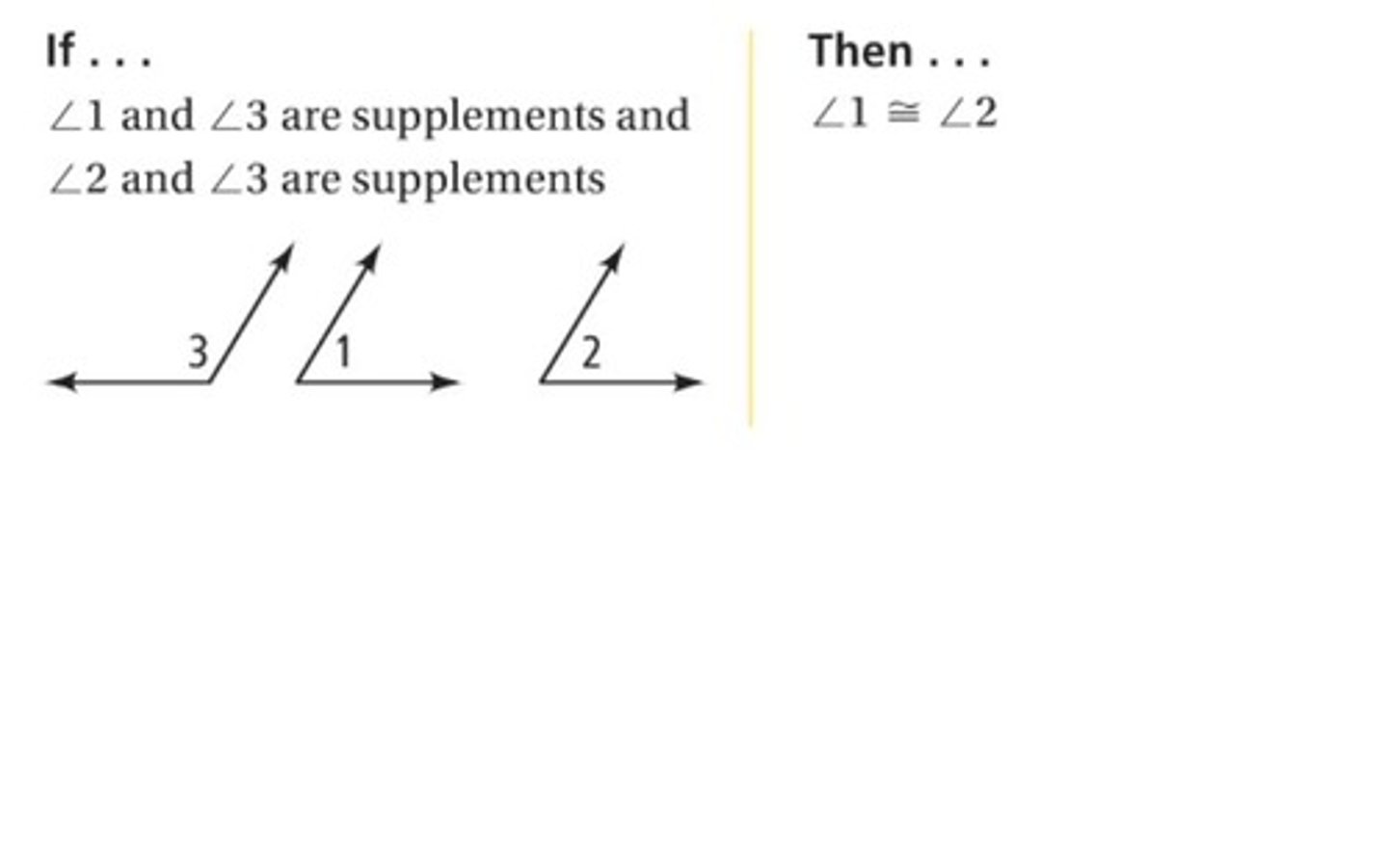
Congruent Supplements Theorem

Angles supplementary to the same angle or to congruent angles are congruent

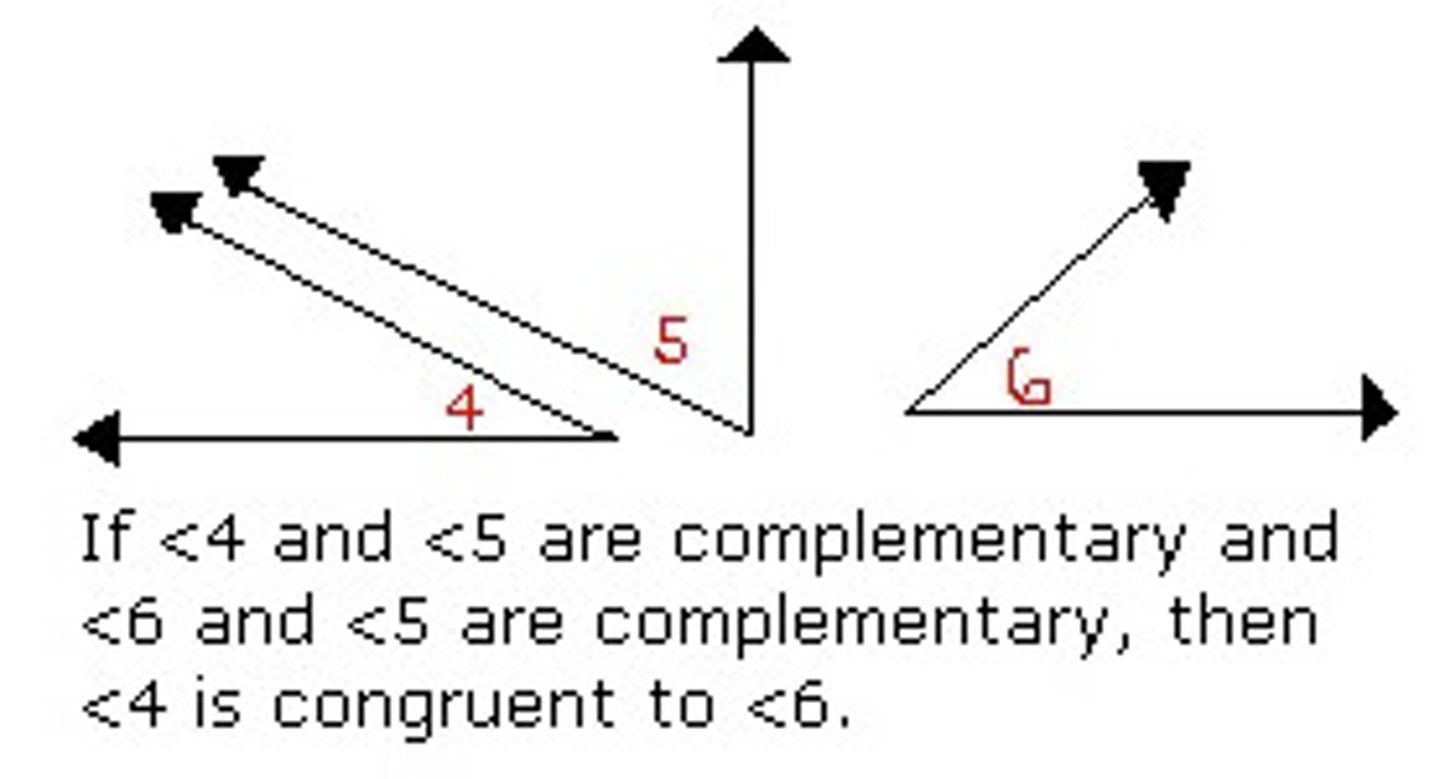
Congruent Complements Theorem

Angles complementary to the same angle or to congruent angles are congruent

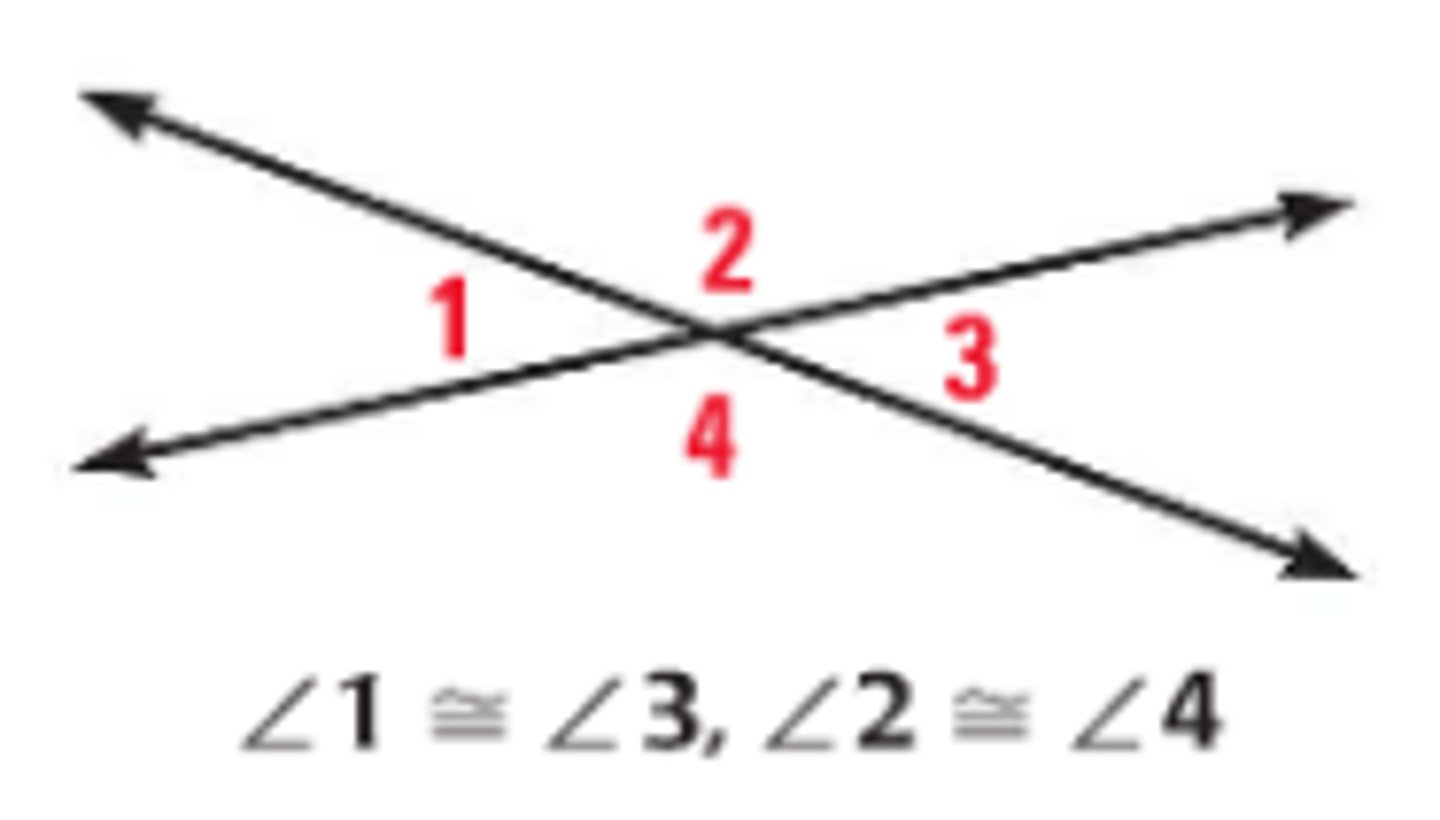
Vertical Angles Theorem

If two angles are vertical angles, then they are congruent.

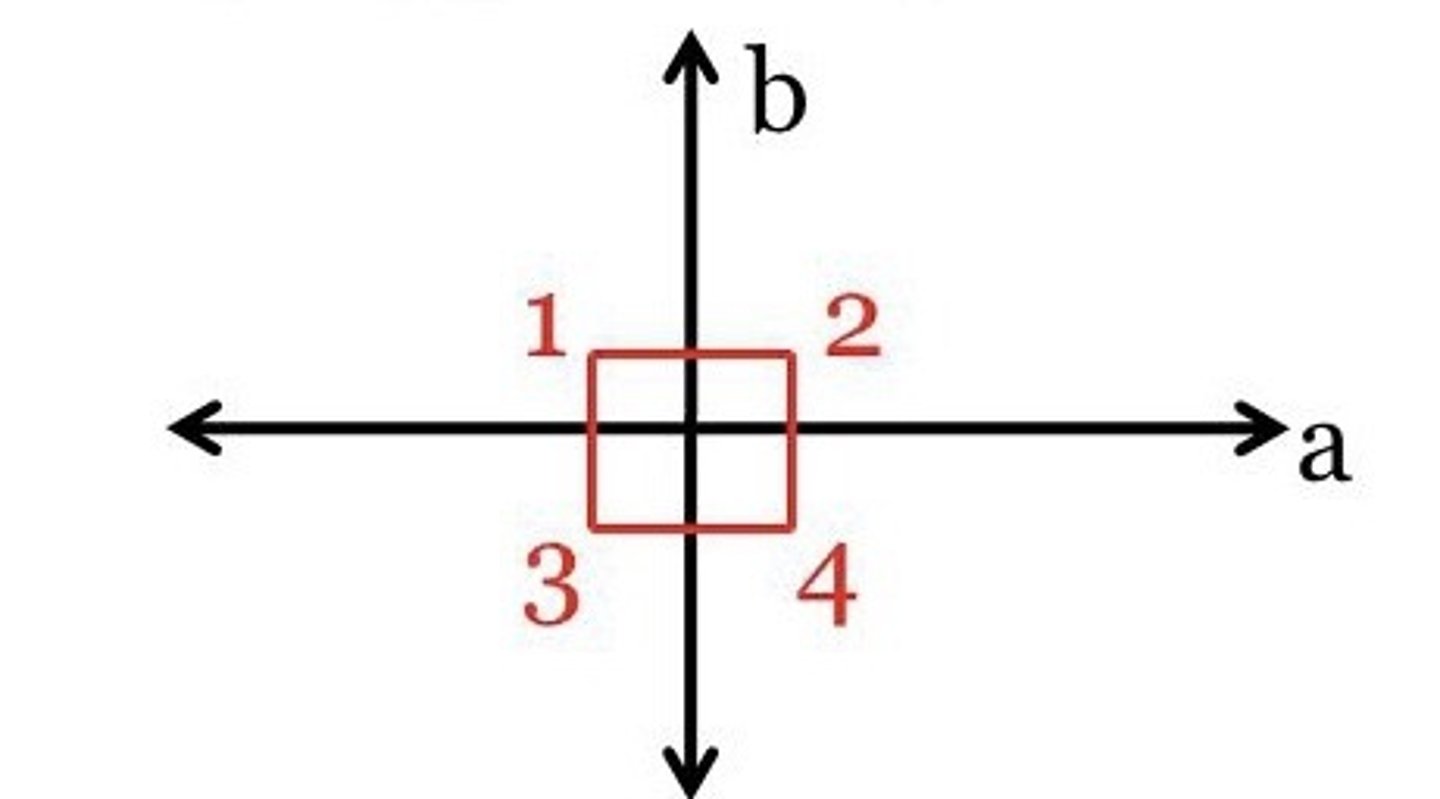
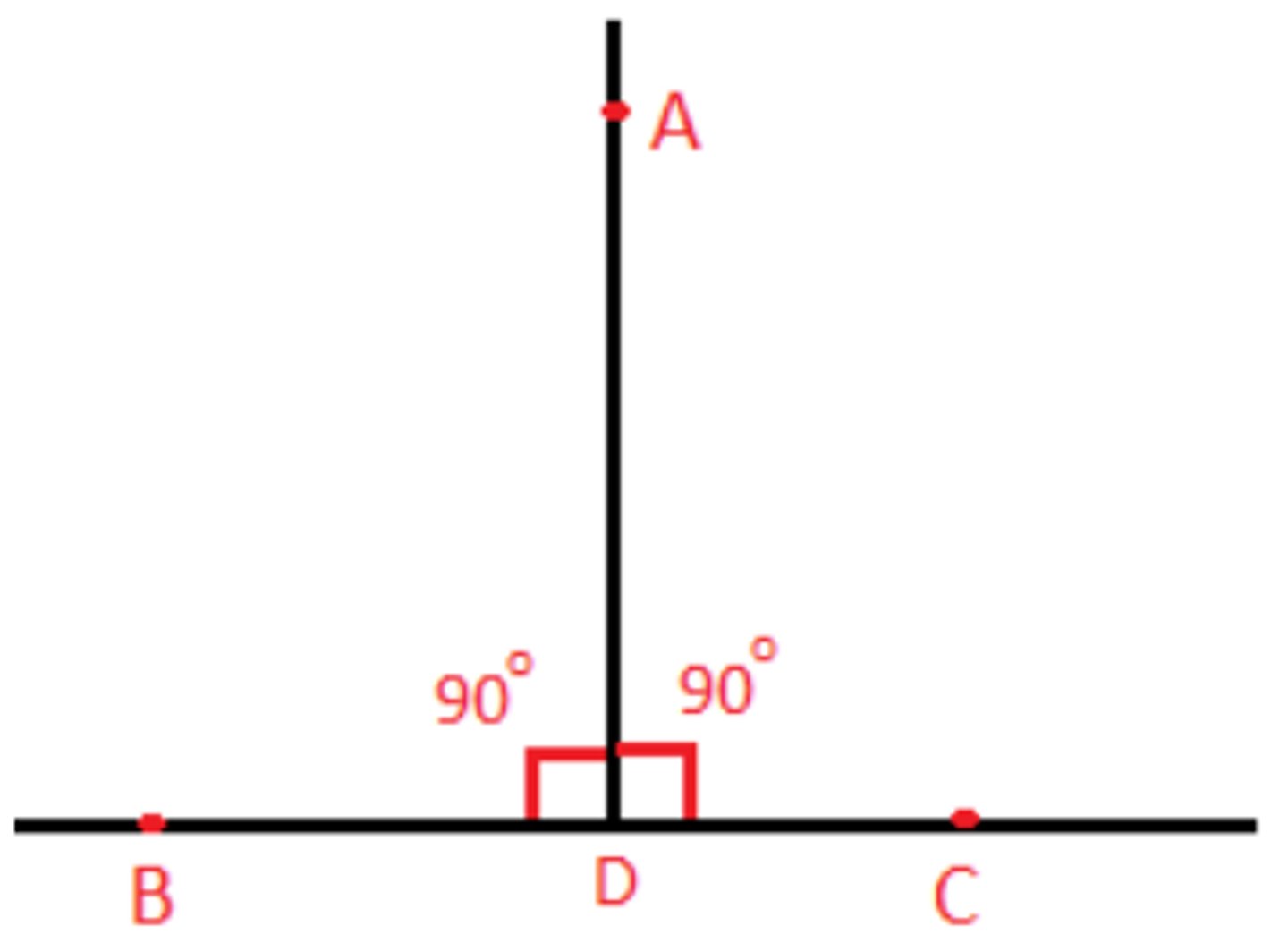
Perpendicular lines intersect

to form four right angles

All right angles

are congruent.

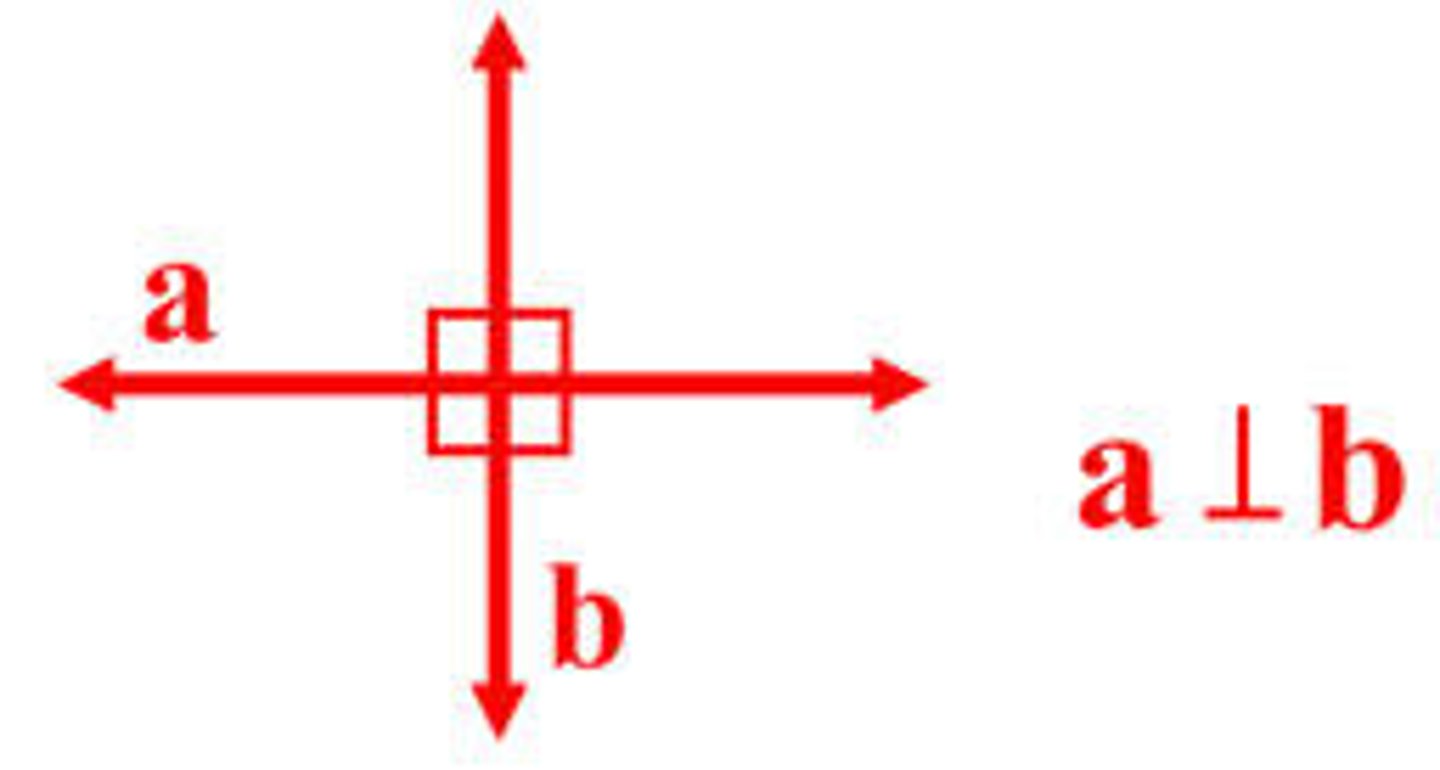
Perpendicular lines form

congruent adjacent angles

If two angles are congruent and supplementary,

then each angle is a right angle.

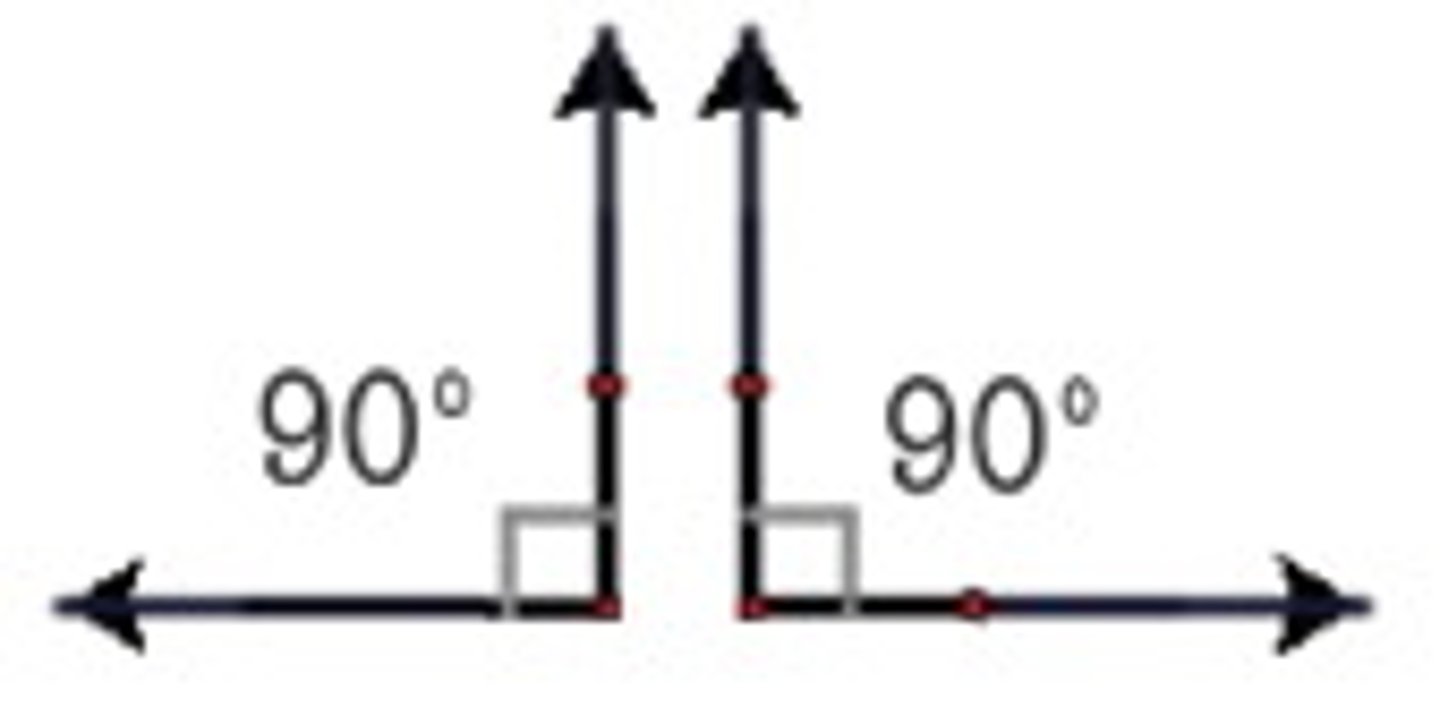
If two congruent angles form a linear pair,

then they are right angles.

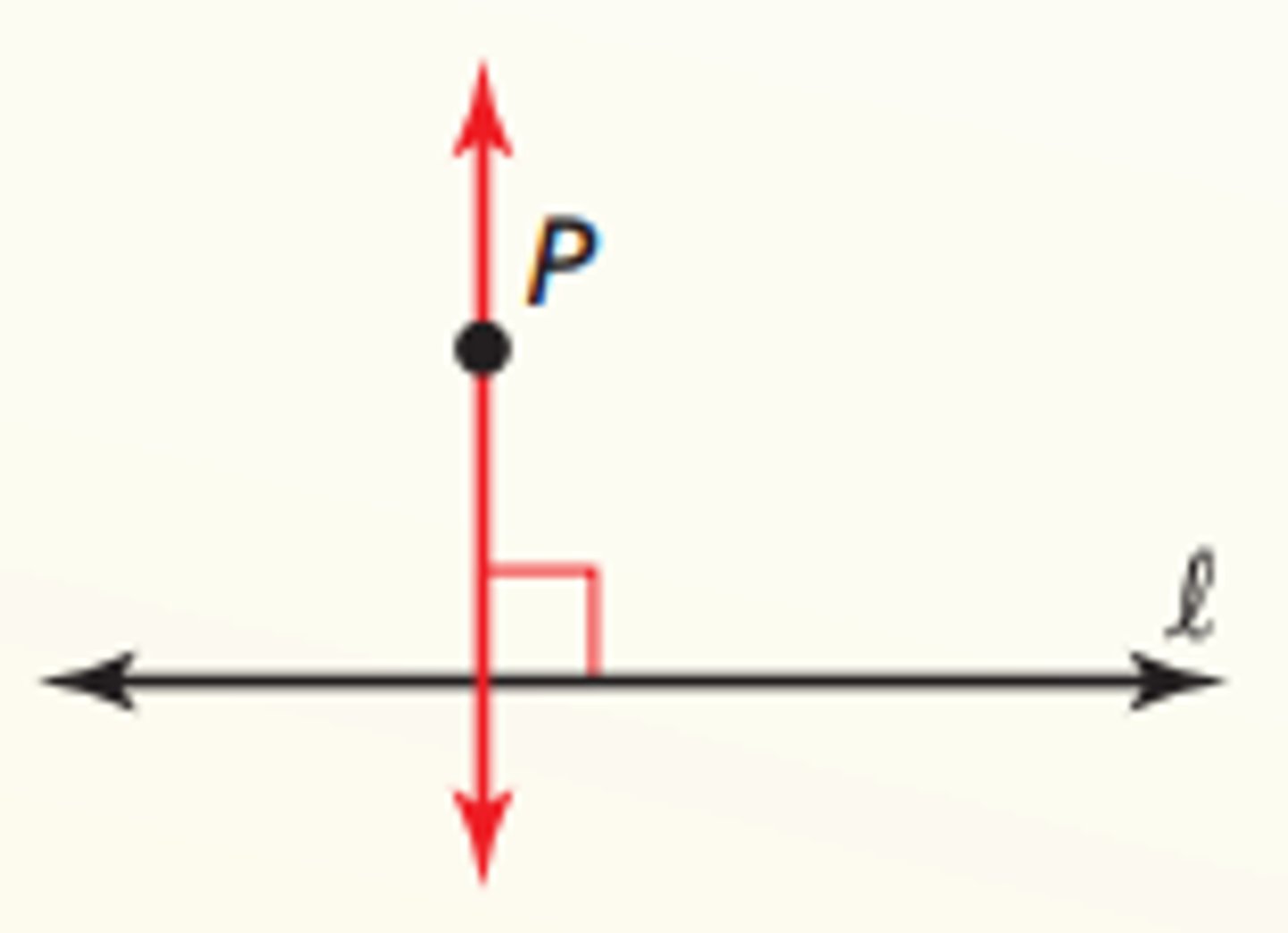
Perpendicular Postulate

If given a line and a point not on the line, then there exists exactly one line through the point that is perpendicular to the given line.

Reflexive Property of Congruence

Symmetric Property of Congruence

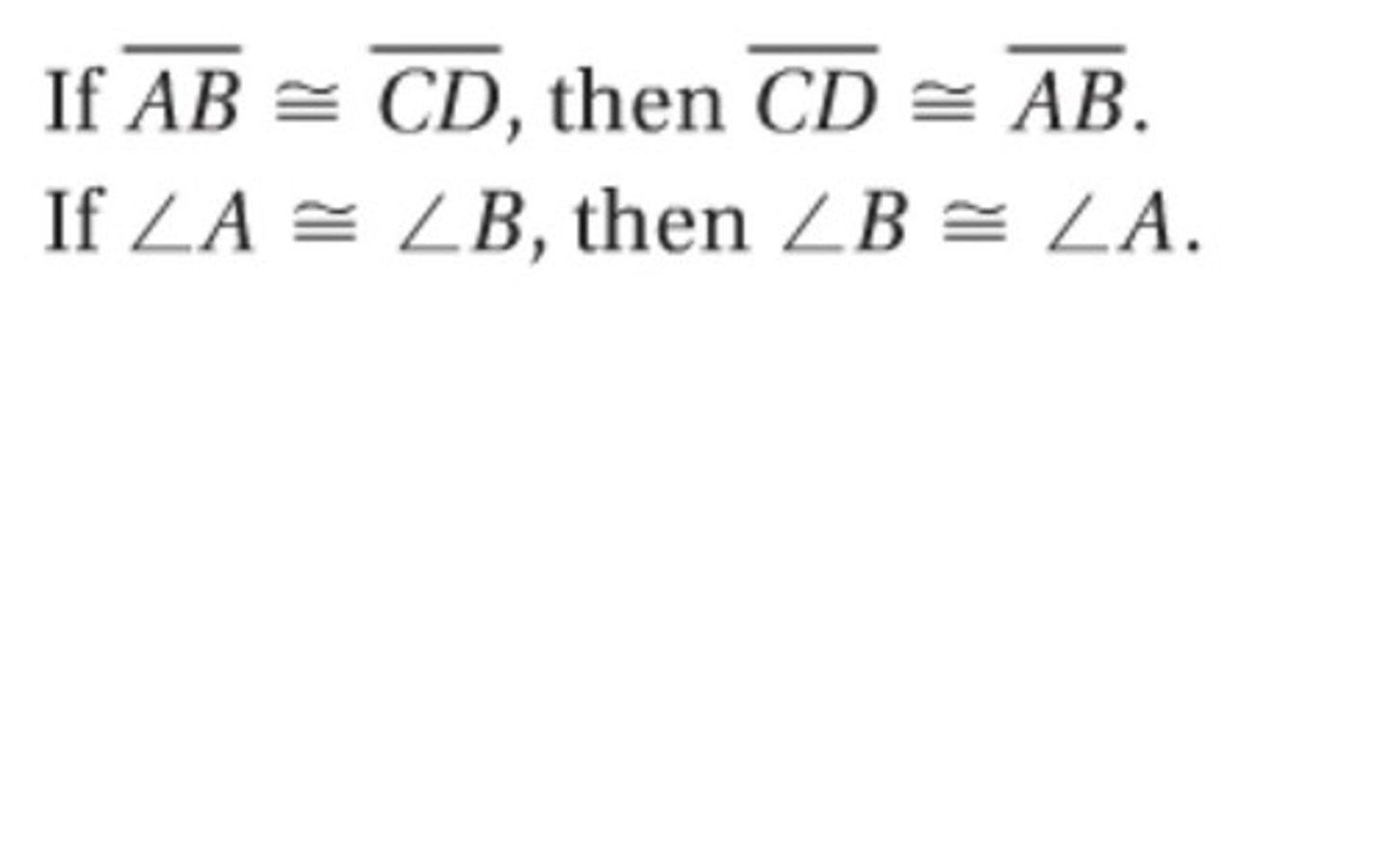
Transitive Property of Congruence

Definition of Congruent Segments

Definition of Congruent Angles