Correlationele onderzoeksmethoden theorie

Populatie

vertegenwoordigt alle individuen die een onderzoeker wil analyseren en waarover hij conclusies wil trekken.

Steekproef

vertegenwoordigt een groep individuen die uit de populatie is geselecteerd.

3 verschillende manieren om een steekproef te trekken

1. simple random sampling

2. stratified sampling

3. Convenience sampling

simple random sampling

alle deelnemers in de populatie hebben een gelijke kans om in de steekproef opgenomen te worden.

Stratified sampling

1. populatie wordt opgedeeld in strata

2. uit elke stratum wordt een volledig willekeurige steekproef getrokken.

Wordt gebruikt wanneer een onderzoeker zeker wilt weten dat elke/bepaalde groep gelijk word vertegenwoordigt in de steekproef.

convenience sampling

steekproef bestaat uit mensen die direct beschikbaar en binnen handbereik zijn. NIET willekeurig.

Waar word beschrijvende statistiek voor gebruikt?

Wordt gebruikt om waargenomen gegevens in de steekproef te beschrijven en samen te vatten. Hoe worden de waargenomen gegevens georganiseerd?

• centrummaten en spreidingsmaten

3 meestgebruikte centrummaten

• Gemiddelde

• Mediaan: middelste waarde

• Modus: score die het vaakst voorkomt

2 meestgebruikte spreidingsmaten

• Variantie: spreiding van waarden

• Standaarddeviatie: gestandaardiseerde maatstaf voor de spreiding van waarden

Waar word inferentiële statistiek voor gebruikt?

wordt gebruikt om conclusies te trekken over het fenomeen dat in de steekproef is waargenomen voor de gehele populatie.

• 2 methoden: null hypothesis significance testing en betrouwbaarheidsinterval schatting

null hypothesis significance testing

toetsen van de nulhypothese en de alternatieve hypothese aan de hand van een significantieniveau (p-waarde)

betrouwbaarheidsinterval schatting

Bij een betrouwbaarheidsinterval van 95%: als er meerdere steekproefen zijn genomen, zou het 95% betrouwbaarheidsinterval in 95% van de gevallen ook de werkelijke waarde bevatten.

• hoe groter de steekproef → hoe meer informatie en nauwkeurige metingen → hoe kleiner het betrouwbaarheidsinterval

Categorische variabelen

variabelen die kunnen worden onderverdeeld in verschillende categorieën. Gebaseerd op kwalitatieve eigenschappen.

kwantitatieve variabelen

niet-vaste groepen, mensen worden gemeten op een continuüm/schaal.

Experimenteel design

• onderzoeker manipuleert 1 variabele om het effect daarvan op een andere variabele te meten

• manipulatie omvat 2 of meer interventies

• bevat, (on)afhankelijke variabelen en een controle

• maakt gebruik van random sampling, matched samples en repeated measures.

Quasi-experiment

• lijkt op experimenteel design, maar maakt geen gebruik van willekeurige sampling

• niet mogelijk om alle variabelen constant te houden

• niet mogelijk om rekening met alle confounds te houden

• interne validiteit is niet sterk, externe validiteit wel

Correlationeel design

• onafhankelijke variabelen worden niet gemanipuleerd

• geen causale conclusies mogelijk

voorwaarden voor pearson’s r

1. onafhankelijk gekozen X en Y (simple random sampling)

2. X en Y zijn lineair gerelateerd aan elkaar

3. geen extreme bivariate outliers

Power

• de kans dat de nulhypothese correct wordt verworpen (wanneer H1 waar is)

• wordt groter bij een grote steekproef

type 1 fout

ten onrechte verwerpen van de nulhypothese op basis van een significant statistisch resultaat, terwijl de nulhypothese in werkelijkheid waar is.

hoe moet je het risico op een type 1 fout beperken?

• crossvalidatie: split de dataset op in twee → vergelijk beide analyses met elkaar → geen effect gevonden in tweede set? type 1 fout

• replicatie: herhaal dezelfde procedure van een onderzoek

• Bonferroni-correctie: oorspronkelijke significantieniveau (\(alpha) delen door het aantal uitgevoerde vergelijkingen. → alfaniveau wordt aangepast en vergeleken met de p-waarde

Gekwadrateerde correlatie (r²)

• gemeenschappelijke variantie tussen X en Y

• Hoe goed kun je de ene variabele voorspellen mbv de andere variabele? (uitgaande van een lineair verband)

indirect verband

X → Z → Y

• X kan Z veroorzaken, Z veroorzaakt Y (Z = mediator)

Spurieus verband

Z → Y

Z → X

Z kan zowel X als Y veroorzaken (er is dus geen verband tussen X en Y).

onderdelen van een eenvoudige lineaire regressie functie

• Y’: voorspelde waarde van Y, gegeven X

• b0: intercept; vertegenwoordigt de voorspelde waarde van Y wanneer iemand 0 scoort op X (constante)

• b1: regressiecoëfficient; verandering in Y’ wanneer X met één eenheid verandert

• b0 en b1 worden ook wel parameters genoemd, omdat we ze schatten

Z-scores

geven aan hoeveel standaarddeviaties een score afwijkt van het gemiddelde

• wordt gebruikt wanneer de interpretatie van de ruwe score niet zo betekenisvol of duidelijk is.

• gemiddelde van 0, SD en variantie van 1

lineair regressiemodel voor Z-scores

de gestandariseerde βbeta variëren van -1 tot 1

• heeft geen intercept

• uitgedrukt in standaarddeviaties

• kan gebruikt worden om effectgroottes van verschillende predictoren binnen één studie te vergelijken

F-test

wordt gebruikt om te testen of de onafhankelijke variabele(n) een significant deel van de variantie van de afhankelijke variabele kunnen verklaren.

• Notatie: F(dfregression, dfresidual) = output

Sum of Squares

• SStotal geeft aan hoeveel scores van de afhankelijke variabele afwijken van het gemiddelde

• vergelijkbaar met R²

• SSregression geeft aan hoeveel de voorspelde scores afwijken van het gemiddelde

• SSresidu geeft aan hoeveel de individuele scores afwijken van de voorspelde scores

  • Dit deel van de variantie kan niet verklaard worden door X (voorspellingsfout)

Waarom is het nuttig om meerdere onafhankelijke variabelen in je lineaire regressie analyse te hebben?

1. Controle: statistisch controleren voor het effect van storende variabelen

2. Theorie: biedt een beter begrip van complexe psychologische eigenschappen

3. Voorspellen: maakt een betere voorspelling van uitkomsten mogelijk

confounder

een variabele die een effect heeft op de afhankelijke variabele (Y) en die ook gerelateerd is aan/varieert met de andere onafhankelijke variabele, waarin je primair geïnteresseerd bent.

• manifesteert zich in een multiple regressie als een groot verschil tussen partiële en semi-partiële correlatie

Controlevariabelen

variabelen waarin je niet primair geïnteresseerd bent, maar waarmee je wel rekening wilt houden met een mogelijke invloed van deze variabelen op de primaire relatie.

• partiële effecten: er is rekening gehouden met andere predictoren

aannames bij het uitvoeren van een multipele regressie

• deelnemers zijn onafhankelijk van elkaar gekozen (simple random sampling)

• Er is sprake van een lineaire relatie

• er zijn geen extreme bivariate outliers

• normaal verdeeld

• homoscedasticiteit: de verdeling van Y, gegeven X, is hetzelfde voor elke X.

• Er is geen interactie tussen X1 en X2

(gekwadrateerde) zero-order correlatie

“gewone” correlatie; van alle variantie in Y, hoeveel % wordt verklaard door X1 in totaal?

• er wordt geen rekening gehouden met andere predictoren, dus gedeelde variantie tussen X1 en X2 worden beschouwd als een onderdeel van X1

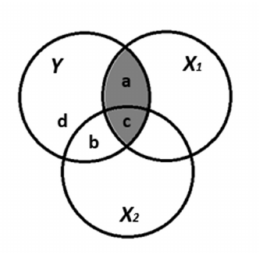
(gekwadrateerde) semi-partiële correlatie

hoeveel van de totale variantie in Y wordt uniek verklaard door X1?

• de correlatie waarin het stuk overlappende variantie tussen X1 en X2 niet is opgenomen.

• Voornamelijk relevant wanneer je wilt weten wat er met de verklaarde variantie gebeurt als X1/ andere predictor wordt weggelaten

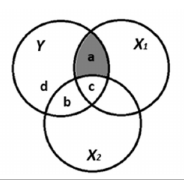
(gekwadrateerde) partiële correlaties

gecontroleerd voor X2 (constant houden), hoeveel % van de overgebleven variantie in Y wordt uniek verklaard door de overgebleven variantie van X1?

• X2 wordt volledig verwijderd uit zowel X1 als Y → dit in tegenstelling tot de semi-partiële correlatie, waar X2 alleen uit X1 wordt verwijderd

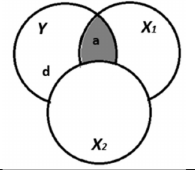
(Waarom) de adjusted R-square (?)

• de gewone R-square zal altijd groter dan 0 zijn in steekproeven, zelfs als er geen verband is → R² overschat de verklaarde variantie in de populatie

• De adjusted R² is dus altijd kleiner dan de normale R²

• heeft soms de neiging om teveel te corrigeren

• veel predictoren + kleine steekproef = grootste verschil R²adj en R²

• predictoren stijgen + constante steekproef = R²adj daalt

• constante predictoren + grotere steekproef = R²adj stijgt

Wat zijn geneste modellen?

je begint met een klein model (1) met weinig predictoren. Je maakt model 2 aan met alle predictoren van model 1 + nieuwe predictoren. Model 1 is dan genest in model 2.

Waarvoor worden geneste modellen gebruikt?

• testen van partiële effect van een cluster van variabelen

• Hiërarchische regressieanalyse (stapsgewijze toevoeging van clusters)

• Testen van partiële effecten van categorische predictoren met 3+ categorieën

• gelijktijdig testen van hoofd- en interactieeffecten van een predictor

referentiegroep

bij het maken van dummy-variabelen is dit de groep die op alles 0 scoort. De RC’s van de andere dummy’s geven de scores ten opzichte van de referentiegroep weer.

interactie

de sterkte van de relatie tussen X en Y is afhankelijk van een derde variabele (Z).

• Wordt in multipele regressie ook wel moderatie genoemd

• Als het interactie-effect niet significant is, veranderen de coëfficienten van de main effecten van betekenis en kunnen ze niet langer rechtsstreeks worden geïnterpreteerd

Simple effects

Wat is het effect van X1 op Y in een specifieke categorie van G?

• geven de hellingshoeken van de regressielijnen binnen elke groep weer

• interactie tussen een continue en categorische predictor

Hoe is een statistisch significante interactie terug te zien in een tabel?

• Statistisch significant: de lijnen lopen niet parallel aan elkaar

• Niet statistisch significant: de lijnen lopen wel parallel aan elkaar

Wat moet je doen als je een MR met interactie tussen kwantitatieve variabelen wilt uitvoeren?

1. centreer de onafhankelijke variabelen (individuele score - gemiddelde van alle scores)

2. Bereken de productterm tussen de variabelen die mogelijk met elkaar interacteren

3. Voor MR uit met de productterm als predictor

Interpretatie van gecentreerde variabelen

• gemiddelde is altijd 0

• De standaardafwijking en variantie van gecentreerde scores zijn hetzelfde als voor de ruwe scores

• Een persoon met een gecentreerde score van 0 heeft dezelfde waarde als de gemiddelde score

• Xvj > 0 → bovengemiddeld

• Xvj < 0 → ondergemiddeld

probing

procedure die wordt gebruikt om de volgende vragen te beantwoorden:

• hoe ziet effect X op Y eruit bij een gemiddelde mate van Z?

• Hoe ziet effect X op Y eruit bij een bovengemiddelde mate van Z?

• Hoe ziet effect X op Y eruit bij een ondergemiddelde mate van Z?

Probing wordt alleen uitgevoerd als het blijkt dat het interactie-effect tussen variabelen significant is.

Multicollineairiteit

doet zich voor wanneer de correlatie tussen onafhankelijke variabelen zeer hoog is en dus veel gemeenschappelijke variantie hebben.

• hierdoor is het moeilijk om de unieke bijdrage van de predictoren aan het verklaren van verschillen in de afhankelijke variabele te beoordelen en ze van elkaar te onderscheiden

• In feite wordt een predictor “twee keer” meegenomen

• schattingen van partiële effecten wordt onnauwkeuriger → grotere standaardfout

Bij multicollineariteit wordt soms als fout gemaakt wanneer afzonderlijke items en de somscore tegelijkertijd in een regressieanalyse worden opgenomen; dit resulteert in perfecte multicollineariteit.

Hoe multicollineariteit detecteren?

• bereken de correlatie tussen predictoren → hoge correlatie kan hoge multicollineariteit betekenen, maar dit is moeilijk te beoordelen

• berekenen van gemeenschappelijke variantie van predictoren

Variance Inflation Factor (VIF)

• veelgebruikte maatstaf voor multicollineariteit

• Als VIF > 6 is er sprake van problematische multicollineariteit (absolute correlatie tussen 2 predictors is 0,913)

• In SPSS zie je onder het kopje tolerance de unieke variantie in een predictor t.o.v. de andere predictoren (dus 1-R²j)

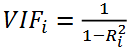
Mogelijke oplossingen voor multicollineariteit

• verwijder de variabelen

• voeg de variabelen samen (totaalscore nemen)

• gebruik een grotere steekproefomvang

• Negeer als je niet specifiek geïnteresseerd bent in partiële correlaties

Binaire logistische regressie

wordt gebruikt om gegevens te analyseren waarvan de afhankelijke variabele binair of een dichotome categorische variabele is.

• Met de analyse onderzoek je de waarschijnlijkheid dat iemand tot één van de twee categorieën behoort.

• Als je hiervoor een linaire regressiemodel zou gebruiken zouden de residuele fouten (voorspellingsfouten) niet normaal verdeeld zijn. Ook zouden er onmogelijke waarden worden gegeven.

Aannames bij een binaire logistische regressie

• De afhankelijke variabele is dichotoom

• De scores van de afhankelijke variabele moeten onafhankelijk van elkaar zijn

• het model is correct gespecificeerd; bevat alle relevante predictoren

• De categorieën van de afhankelijke variabele zijn uitputtend en sluiten elkaar uit

Onderdelen van de logistische functies

• 𝑒 = 2.718282 (grondtal van de natuurlijke logaritme)

• Dit is een S-vormige functie (sigmoïdaal; dus niet-lineaire functie), met uitkomsten tussen 0 en 1

• 𝑏0 en 𝑏1 zijn de logistische (regressie)coëfficiënten

• b1 bepaalt hoe steil de functie verloopt en de functie stijgt of daalt.

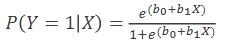
logistische functies bepalen in empirische gegevens

• Logistische functie is een niet-lineaire functie. We kunnen niet zomaar lineaire regressietechnieken (bijv. kleinste kwadraten schattingen) toepassen.

• Lineaire functies zijn wel makkelijker

• Je kunt van een logistische functie een lineaire functie maken door een aantal stappen

  • 1. kansen naar odds omrekenen

  • 2. logaritme nemen van odds (logit)

Interpretatie van odds

Hoeveel groter is de kans op Y = 1 dan op Y = 0?

• Om dit te berekenen, kun je de verhouding tussen 1 en 0 berekenen

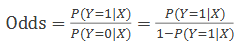
van odds naar logit

Logit is de natuurlijke logaritme van de odds ratio, en daarmee een lineaire functie van X.

• Nadeel hier is dat de afhankelijke variabele (= logit) lastiger voor te stellen is. want hoe moet je een verandering van 5 eenheden in de logit voorstellen. → gebruik daarom de logit om kansen of odds te berekenen om zo de interpretatie duidelijker te maken

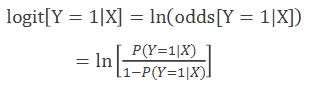
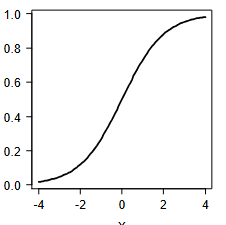
wordt in deze grafiek kansen, odds of logit afgebeeld?

kansen; het is een s-curve

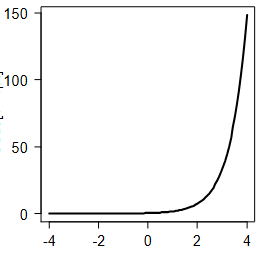
wordt in deze grafiek kansen, odds of logit afgebeeld?

odds; wanneer je kansen omrekent naar odds krijg je een exponentiële functie

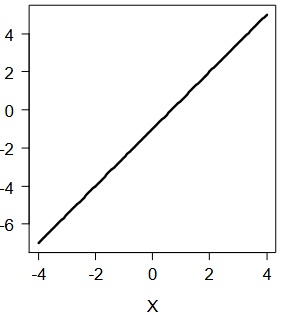
wordt in deze grafiek kansen, odds of logit afgebeeld?

logit; wanneer je van de exponentiële functie van odds het natuurlijk logaritme neemt, krijg je een lineaire formule.

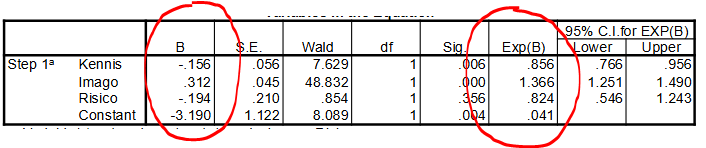
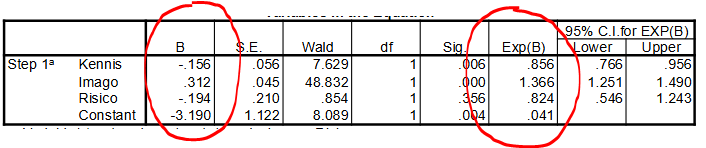
coëfficienten in multiple logistische regressie met continue onafhankelijke variabelen

• Regressiecoëfficiënten B beschrijven de partiële effecten (= onder constant houding van de rest) in termen van veranderingen in de logit

• Regressiecoëfficiënten Exp(B) beschrijven de partiële effecten in termen van veranderingen (factor) in de odds

• Alleen de trend van de kans kan worden omgeschreven; het is niet mogelijk om iets te zeggen over de omvang, toename/afname van de odds

pseudo-R kwadraatmaatstaven

ruwe maten die aangeven hoe goed een model verschillen in de afhankelijke variabelen verklaart.

• Cox & Snell heeft als nadeel dat het nooit 1 kan worden

• Nagelkerke R² kan wel de waarde 1 aannemen en is altijd hoger dan C&S

classificatietabellen

gebruikt wanneer je wil bepalen hoe goed de voorspellingen in de steekproef zijn.

• hoe lager de fouten, hoe beter

• Maak alleen gebruik van classificatietabellen als je het geschatte model ook ‘echt’ gaat gebruiken om in de toekomst personen te classificeren

• De classificatietabel geldt alleen voor de gebruikte cutoff (in het voorbeeld 0.50). Bij andere waarden voor de cutoff (bijv. 0.80) veranderen ook de classificatiefouten.

• Classificatietabellen zijn niet geschikt om ‘model fit’ te onderzoeken; het toevoegen van predictoren hoeft niet persé tot minder classificatiefouten te leiden.

• Bovendien zijn classificatietabellen ‘populatieafhankelijk’; dit betekent dat het model goed voorspelt in de ene populatie, maar misschien minder goed in een andere populatie.

effect coding (dummy’s)

een methode voor het weergeven van categorische variabelen in regressiemodellen, waarbij -1, 0 en 1 worden gebruikt om groepsgemiddelden te vergelijken met het totale ongewogen gemiddelde van alle groepen