D1 Gravitational fields

grav fields

D1.1 Newton’s law of gravitation

Gravitational force between 2 bodies outside a uniform field; earth-sun → The gravitational force between two point masses is ∝ to m₁m₂ and inversely ∝ to the square of their separation (r²)

F = ^{GM₍₁₎m₂}/_r² = force felt by either body.
G = Newtons Gravitational Constant: 6.67×10^-11 Nkg^-2m²
r = distance centre mass 1 mass 2

D1.2 Gravitational Field Strength

Force due to gravity = weight
Gravitational field: region of space where test mass experiences force due to grav. attraction of another mass.
ALWAYS ATTRACTIVE!!!
grav field strength = force per unit mass experienced by test mass at that point → g = ^F/_m2 = ^GM₍₁₎/_r²
M causes grav field, all bodies at same r² receive same grav field stren

D1.3 Uniform sphere → point mass

Uniform sphere; point mass → uniform distribution of mass (density)
→ field lines are uniform around sphere and thus around point mass

D1.4 Field lines

Directed towards centre of mass. Size of field proportional to line density. Direction shows acceleration of acceleration of point mass put into the field.
Point mass: radially inwards: non uniform field; line density ∝ field
Earth’s surface (straight and faaar): par. lines spaced equ:uniform field

D1.5 Grav Potential

V = W done per unit mass in bringing test mass from ∞ to defined point
J kg^-1. ALWAYS negative: attractive force. at ∞, V = 0, so work must be done to reach infinity, and work is “released” when “falling” to defined point. As object moves away from “planet” - less increases.

V_g = - ^GM/_r
r = distance centre of mass to point mass.
SCALAR
In uniform field: ΔV = g Δh

D1.6 Grav Pot Energy

In non-uniform field (g depends on r)
GPE - energy objects possesses due to position in field
→ Work done in bringing mass from ∞ to point

Near earth surface: uniform field: E_p = mgΔh: work done to lift object
non unif. field: ΔGPE = W = mΔV_g (m=of small object)
Change in ΔE_p = W = GMm (¹/r₁ - ¹/r₂)
E_p = -^GMm/_r = -Fr (as we known, as work done = Fr)
Graph F - r : area = work done

D1.7 Grav Pot gradient

g at a particular point = -(gradient of a V-r graph at that point)
g = - ^ΔV_g/_Δr (g = positive…)

D1.8 Grav Equipotential surfaces

Equipotential lines: like wavefronts; perpendicular to field lines

All points on one line have same grav potential.

Dotted lines, no arrows

Uniform field = uniform ditance

No work is done when moving along an equipotential line/surface ( eg. earths surface)

ΔV = 0.

D1.9 Keplers 1st law of planetary motion

SHAPE 1^st law: orbit of a planet is an ellipse and sun is at one of the 2 foci (focus is at point where red distance is constant throughout ellipse.)

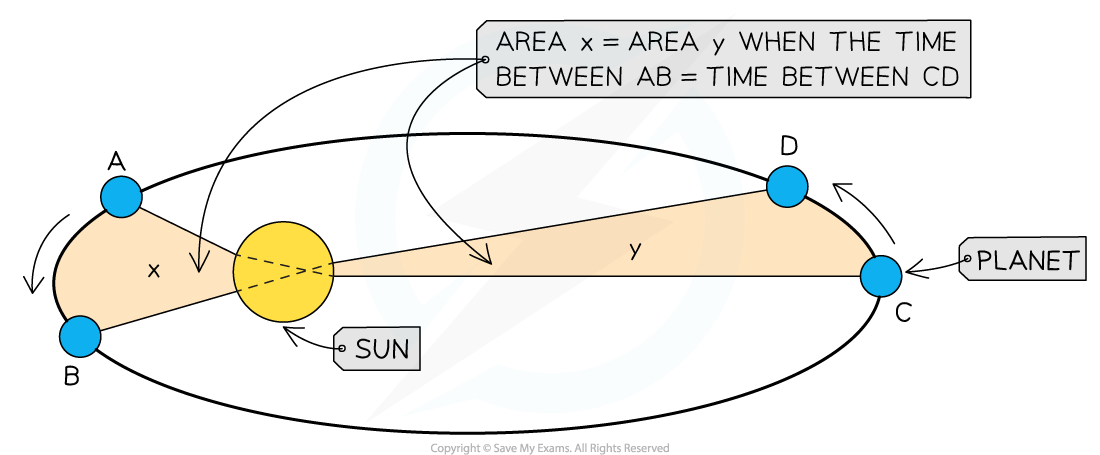
D1.10 Keplers 2nd law

MOTION 2nd law: all line segments joining sun to planet sweep equal area in equal time intervals.
Shows that planets move faster near sun and slower further away from it.

D1.11 Kepler’s 3rd law

3rd law: For planets/satelites in circular orbit about same body; Time period² ∝ radius of orbit³

2 log T ∝ 3 log r

D1.12 Time period and orbital radius relation

v = ^2πr/_T
v² = (^2πr/_T)² = ^GM/_r (centripetal force)
→ T² = (4π²r³)/_GM

D1.13 Escape speed

Minimum v alowin object to escape grav. field with no other E _input

Same for all masses in same grav. field.
½ v_esc² = ^GM/_r (E_k = energy/m needed to overcome grav potential energy up to infinity = -E_p)
v_esc = √ (^2GM/_r)

Rockets launched from earth surface dont need to achieve escape v to reach orbit around earth; continuously fueled, not whole field is escaped, only to get to its orbit (centripetal force keeps it spinning)

D1.14 Orbital speed

Most planets/satelites have near circular orbits; F_g → F_centripetal
Both F_g & F_c are perp to direction of travel.
F_g = F_circ
^GMm/_r² = mv²/_r
v_orb = √ (^GM/_r) ——no matter mass of plan/sat, same v_orb
r = centre of M to satellite.

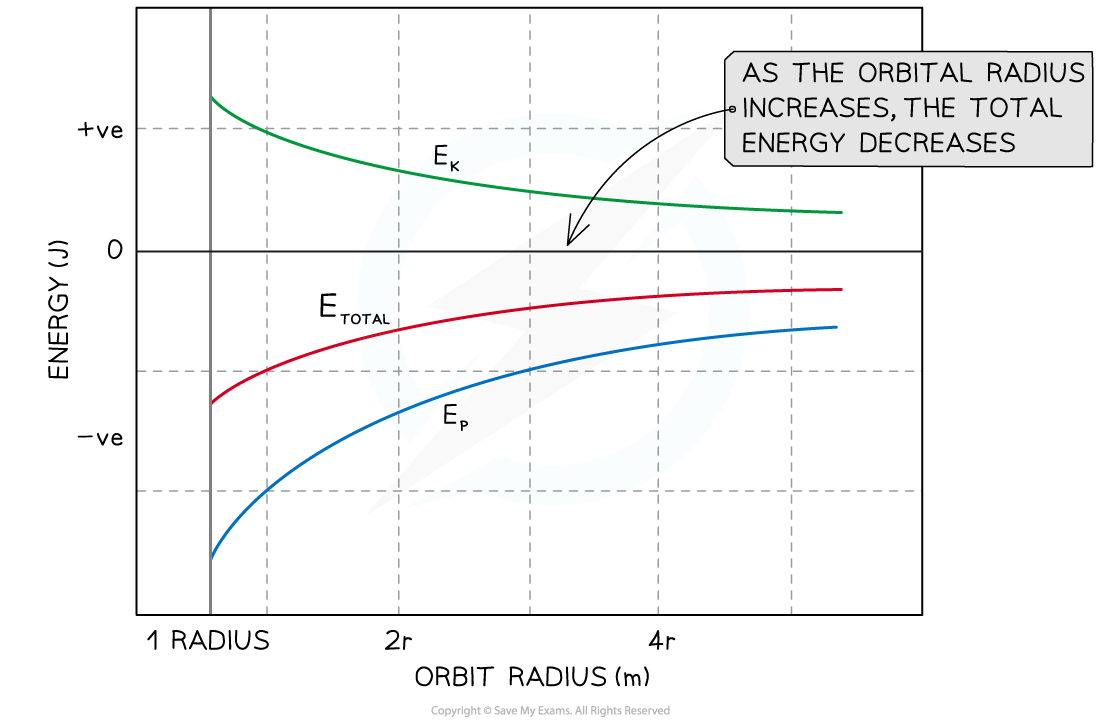
D1.15 Orbital Energy

E_T = E_k + E_p
E_p = -2E_p
E_T = -E_k = ^E_p/₂

D1.16 Drag in orbital motion

In low orbits (<600km), satelites may experience viscous drag (air

very small, but over time has signif. on height and speed of orbit

get closer to earth until hits it (radius decreases, v increases)
E_k → Q (friction air particles and surface of satellite.