Stat 1000 - Class 1,2 (Unit 1)

Statistics

Set of methods for obtaining, organizing, summarizing, presenting and analyzing data

Data

Comes from characteristics measured on individuals, or units

Individuals/ Units

Nearly anything: people, animals, places, things, etc

Observations

collected data values

Population

Totality of individuals about which we want information

Sample

Subset of the individuals in a population that we actually examine in order to gather information

Good sample

Representative of the populations

Identifying the population that a sample represents

replace the sample size with “all”

Variable

characteristic or property of an individual.

Examples of possible variables

Lifespan of a light bulb, The number of heads in five tosses of a quarter, Hair colour

Classifications of data

categorical and quantitative

Categorical data

• values of categorical/qualitative variables.

• These are variables that place individuals into one of several groups categories.

Categorical variables (examples)

• Eye colour

• Favourite singer

• Reason for taking STAT 1000

Categorical and ordinal

meaningful, logical ordering to the values of a categorical variable.

Categorical and nominal

not a meaningful, logical ordering to the values of a categorical variable

Quantitative data

Represents quantitative variables

Quantitative variables are

Take numerical values for which arithmetic operations (such as subtracting, averaging, etc.) make sense (i.e. their results are meaningful).

Quantitative variables (examples)

• Height

• Volume of air in a balloon

• Exam score

• Time

Data distribution tells us:

What values a variable takes, and How often it takes these values

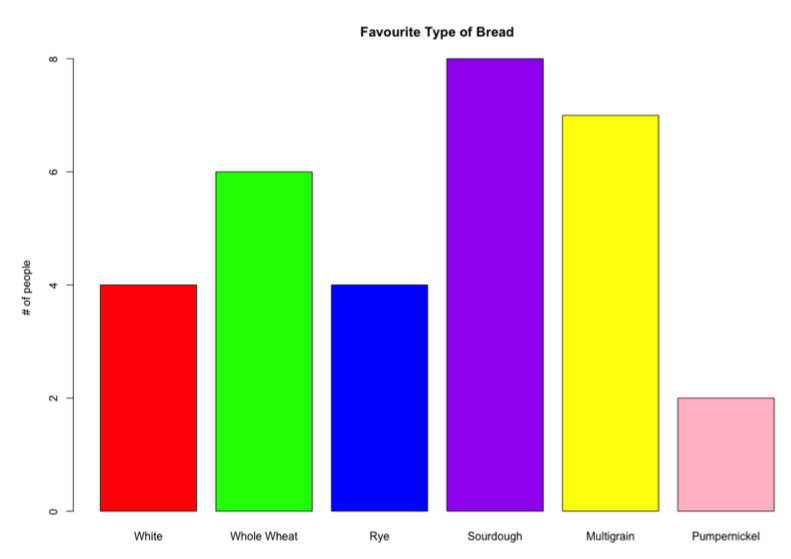
Bar Charts

Display variable values on one axis, and frequencies on the other.

• Bars don’t touch (not continuous)

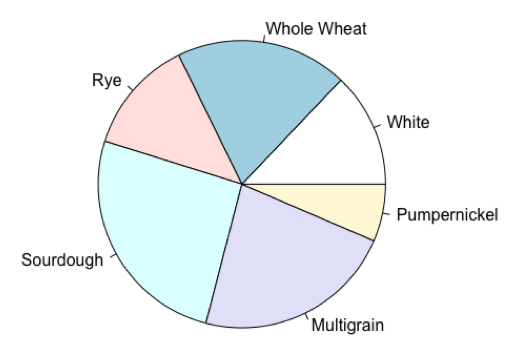
Pie charts

visual representation of the relative frequency/proportion of the observed values for a categorical variable

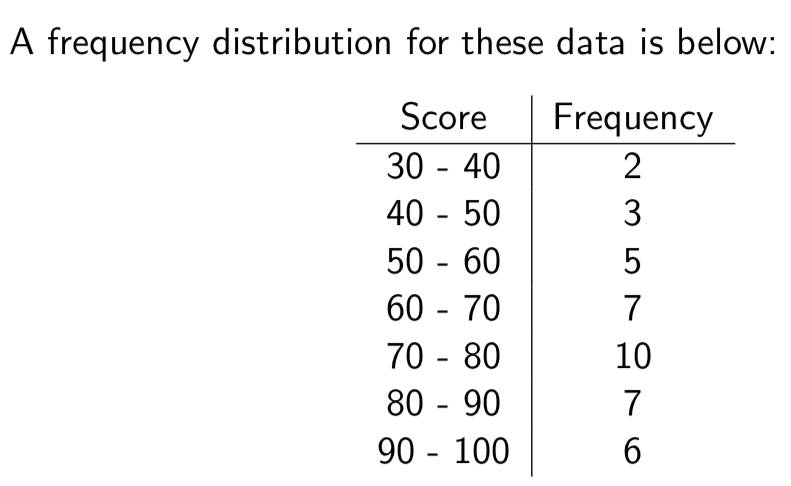
Frequency distribution

count of how many of our data values fall into various predetermined classes or intervals

Frequency Distribution Example

Relative frequency distributions

Dividing the number of data values in each class by the total number of data values, we get the relative frequency, or proportion of individuals in each class

Proportions (relative frequency distributions)

Values between 0 and 1 that are decimal representations of fractions. You can convert proportions to percentages by multiplying by 100.

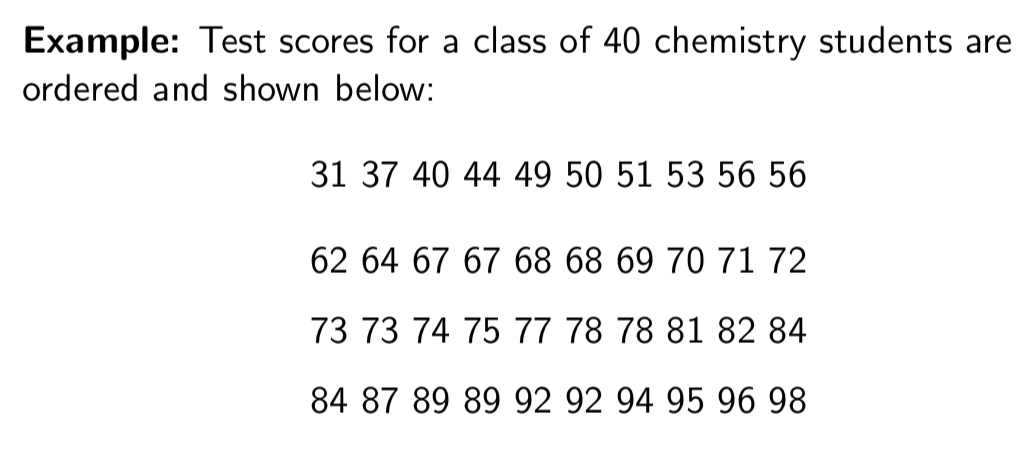
Relative frequency distribution Example

Frequency distribution (intervals)

• choose them ourselves

Frequency distribution (interval rules)

• Our first interval must include the lowest data value (called the minimum)

• Our last interval must contain the highest data value (called the maximum)

• All intervals should be of equal length

• Each interval includes the left endpoint, but not the right

Choosing the intervals (frequency distribution)

“nice choices”, that summarize our data well. We’d typically use around 5 - 10 intervals total

Why cant we just use non-overlapping intervals?

because of decimals (continuous variables)

• 70-79 how about 79.5?

Continuous variables

These are quantitative variables that can take any value within a given range.

Continuous variables (examples)

Test scores, age, height, distance

Discrete variables

These are quantitative variables that can only take a “countable” number of values: i.e. they can only take a specific, distinct values.

discrete variables (examples)

• The number of children in a family

• The number of days of rain in a month

• The number of books a person has read in their life

Histograms

More useful and commonly used display of continuous data

• Graphical displays of the frequency (or relative frequency) of data values falling into each of several intervals.

• Histograms are especially useful when we’re dealing with large data sets.

What type of data is used for a histogram

continuous, quantitative data

Why is there no spaces between the bars in a histogram

because they are continuous data

What does the base of a histogram represent

length of the interval (equal length)

What does the height of a histogram represent

the frequency of the data in each interval

Distribution shape (histogram)

A histogram can be used to characterize the shape of the data distribution

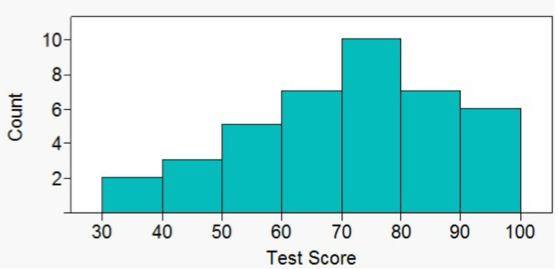
• Symmetric

• Skewed to the right

• Skewed to the left

Symmetric shape (histogram)

center divides it into two approximate mirror images

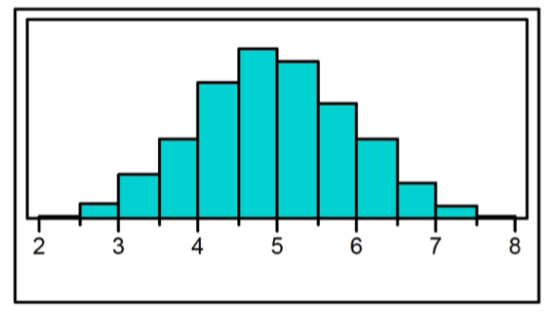
Skewed to the right (Histogram)

longer tail on the right side

• most of the data values are concentrated on the left

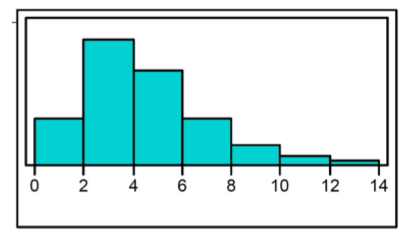
Skewed to the left (Histogram)

longer tail on the left side

• most of the data values are concentrated on the right.

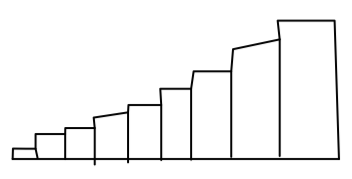
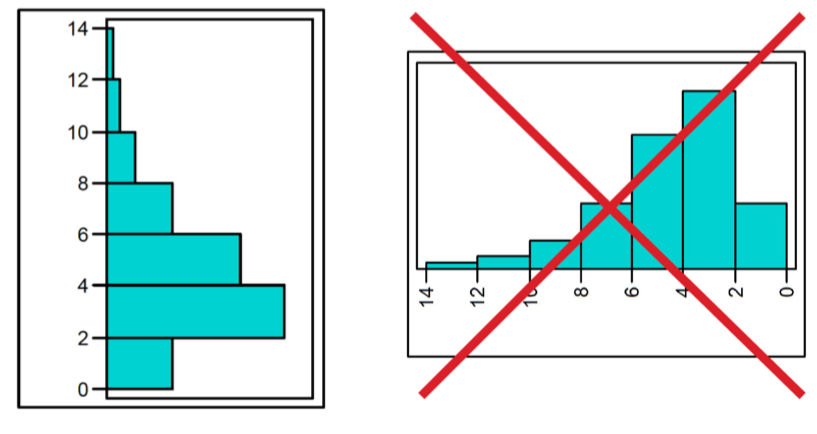
Distribution shape (!!WARNING!!)

Be careful interpreting the shape of a histogram if it’s displayed vertically!!

• x-axis has to start at 0 (when flipped horizontal)

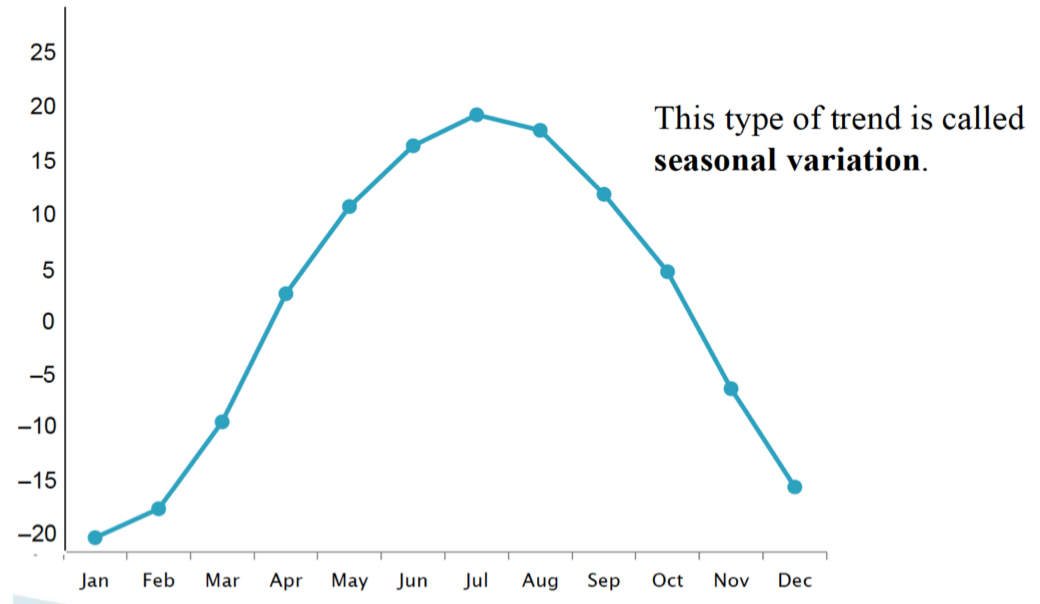
Time series data

which are values for a variable measured over time

How can you visually display time series data

time plots

What constitutes a Time Plot

Time is plotted on the x - axis, and variable values are plotted on the y - axis

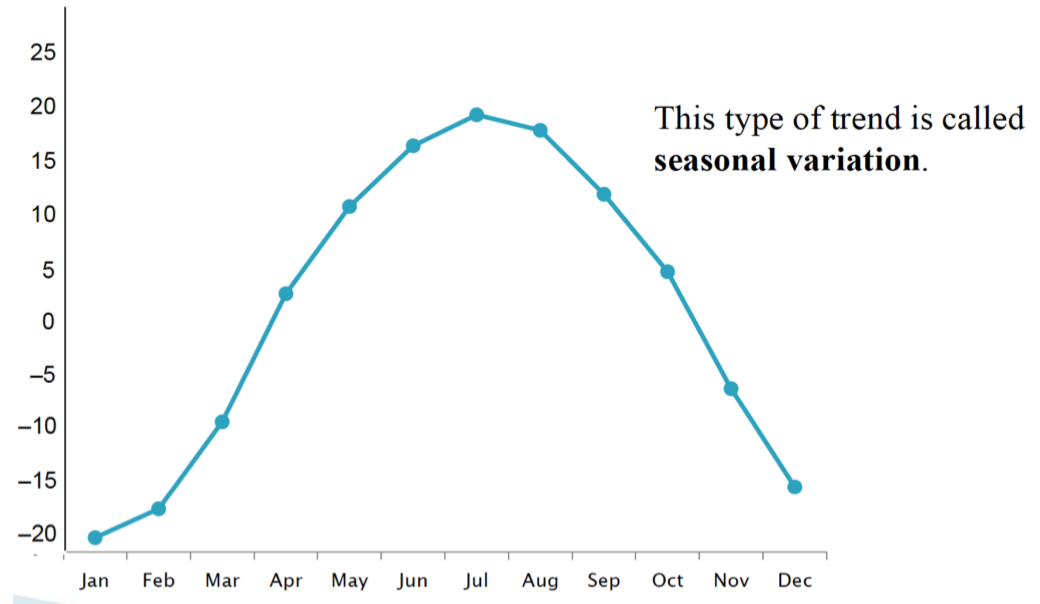
How is data represented on a Time Plot

Data values are represented by points. We connect these points to better visualize the pattern/trend.

Seasonal variation (time plot) {example}

fluctuations in data values that occur at regular intervals due to seasonal factors, showing predictable changes at specific times of the year.