symmetry of functions w/ even and odd functions

Symmetry with respect to the Y axis

(x,y) > (-x,y)

X changes to opposite

Symmetry with respect to the X axis

(x,y) > (x,-y)

Y changes to the opposite

Symmetry with respect to the origin

(x,y) > (-x,-y)

Both X and Y changes to the opposite

How to test for symmetry in an expression?

Replace the x and y in the equation with the corresponding negative x’s and y’s you need to substitute based on the type of symmetry you are testing

Make sure the new equation matches the original for the testing to prove the symmetry.

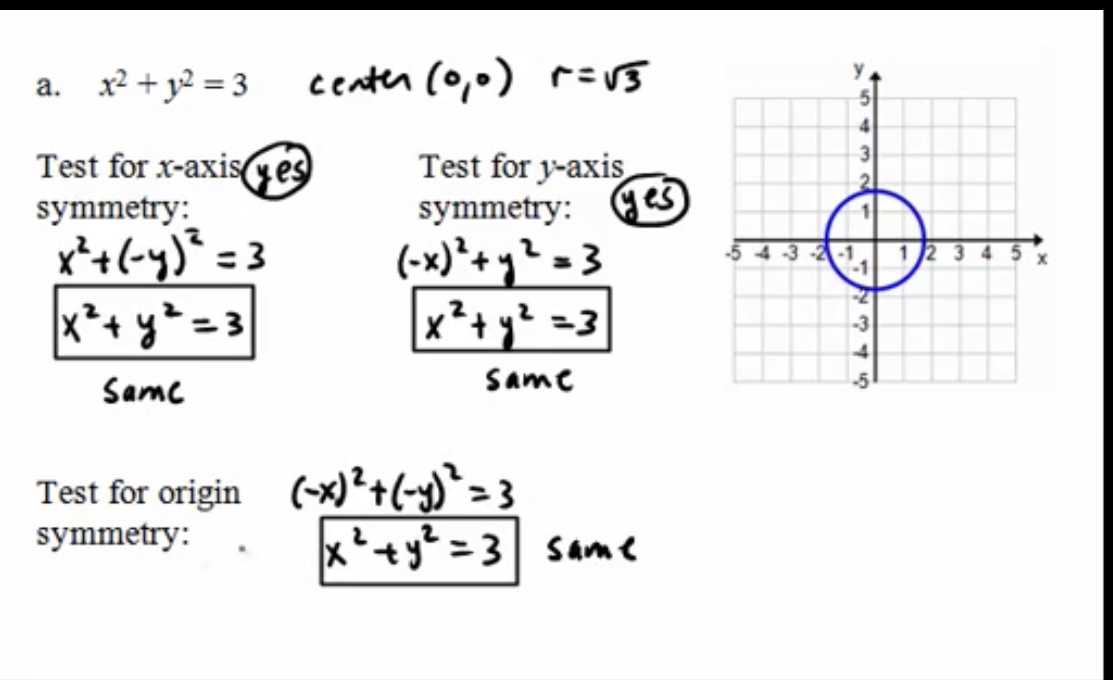
When substituting negatives (-x) or (-y) into equations to find the symmetry, what must you know about the exponents?

Exponents that are odd will stay negative

Exponents that are even will be positive

When squared it will be even (-x)² — > x²

When cubed it will be odd (-x)³ — > -x³

How to test for symmetry for graphs?

Find points/lines/curves on one plane and see if it can match the same coordinates on any of the other 3 planes in a way it’s considered symmetrical with altering negatives.

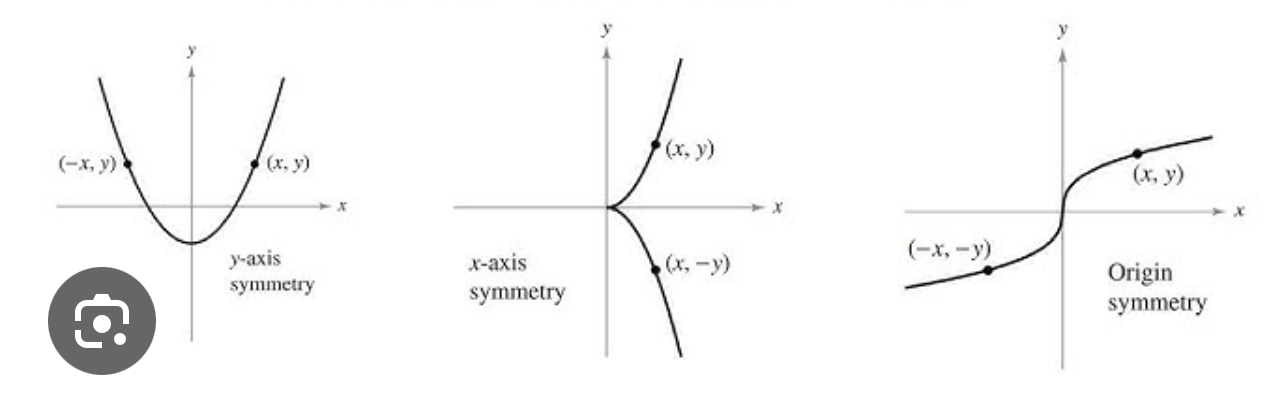
Even and odd functions type of symmetry, and which type of symmetry is considered neither even or odd?

X axis symmetry is considered neither even or odd

X