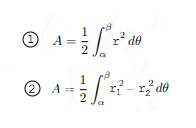Engng Math 145 Polar Coordinates

Polar coordinates

(r, θ), where r is distance from origin to point & θ is angle between x-axis and line.

Measuring conventions

• θ > 0: measure angle anti-clockwise

• θ < 0: measure angle clockwise

• (-r, θ) = (r, θ+π)

• (0, θ) is a single point

Conversion from Cartesian to Polar coordinates

Cartesian→Polar:

• Use r = sqrt(x² + y²) & tanθ = y/x

Polar→Cartesian:

• Use x = rcosθ & y = rsinθ

Plot point in Cartesian before determining Polar.

Polar curves

Graph of a polar eqn r = f(θ) consists of all points P that have at least one polar representation (r, θ), with coordinates r & θ that satisfy the polar eqn.

Differentiation with polar curves

For polar curve r=f(θ) can be seen as parametric curve, where

x = rcosθ = f(θ)cos(θ) & y = rsinθ = f(θ)sin(θ), therefore →

Integration with polar curves

1. For lines θ=a & θ=b and curve r=f(θ)

2. For lines θ=a & θ=b and curves r₁=f(θ) & r₂=g(θ), r₁ > r₂