`Introduction to Vector Calculus

What is a scalar quantity?

A scalar has only magnitude and sign, represented by a single number.

What is a vector quantity?

A vector has both magnitude and direction.

How is a vector represented in 2D Cartesian coordinates?

\mathbf{v} = \begin{pmatrix} \mathbf{v}_x \\ \mathbf{v}_y \end{pmatrix}

How is a vector represented in 3D Cartesian coordinates?

\mathbf{v} = \begin{pmatrix} \mathbf{v}_x \\ \mathbf{v}_y \\ \mathbf{v}_z \end{pmatrix}

What is the magnitude of a 3D vector \mathbf{v}?

|\mathbf{v}| = \sqrt{\mathbf{v}_x^2 + \mathbf{v}_y^2 + \mathbf{v}_z^2}

What is a unit vector?

A vector of magnitude 1: \hat{v} = \dfrac{\mathbf{v}}{|\mathbf{v}|}.

What does the unit vector represent?

The direction of the vector with a magnitude of 1

What is the zero vector?

A vector with zero magnitude and no defined direction, denoted \mathbf{0}.

What are the standard unit basis vectors in 3D?

\mathbf{i} = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix},\;\mathbf{j} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix},\;\mathbf{k} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}

How is vector addition defined for \mathbf{v}_1 = \begin{pmatrix} \alpha \\ \beta \\ \gamma \end{pmatrix}

and \mathbf{v}_2 = \begin{pmatrix} a \\ b \\ c \end{pmatrix}

?

\mathbf{v}_1 + \mathbf{v}_2 = (\alpha + a,\; \beta + b,\; \gamma + c)

How is scalar multiplication defined for a\in\mathbb{R} and \mathbf{v}=(\alpha,\beta,\gamma) ?

a\mathbf{v} = (a\alpha,\; a\beta,\; a\gamma)

List key vector algebra properties.

Commutative and associative addition, distributive laws, additive identity, additive inverse.

What is a 2\times2 matrix?

An array of 4 scalars

M = \begin{bmatrix} a & b \\ c & d \end{bmatrix}

Define a 2\times2 matrix–vector product.

\begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{pmatrix} \alpha \\ \beta \end{pmatrix} = \begin{pmatrix} a\alpha + b\beta \\ c\alpha + d\beta \end{pmatrix}

What is the 2D rotation matrix for angle \phi?

\begin{bmatrix} \cos\phi & -\sin\phi \\ \sin\phi & \cos\phi \end{bmatrix}

What is the determinant of a 2\times2 matrix?

\det(M) = ad - bc

Geometric meaning of \det(M) for 2\times2 ?

Area scaling factor; if \det(M)=0 the map is non-invertible.

Give a 3\times3 determinant formula (cofactor along first row).

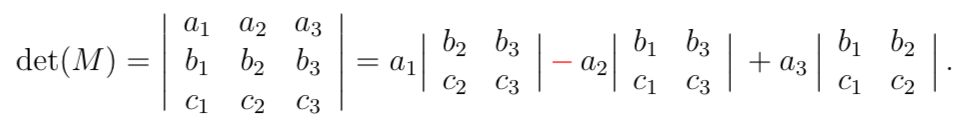
Geometric meaning of a 3\times3 determinant?

Volume scaling factor; non-zero means invertible.

Define the scalar (dot) product.

\mathbf{v}_1 \cdot \mathbf{v}_2 = |\mathbf{v}_1|\,|\mathbf{v}_2|\cos\theta

Where \theta is the angle between the two vectors.

Also equivalent is v1=(a,b) v2=(x,y) then the cross product is (ax,by) and the same applies in 3d vectors

Dot product in components (3D).

\mathbf{v}_1 \cdot \mathbf{v}_2 = \alpha \mathbf{a} + \beta \mathbf{b} + \gamma \mathbf{c}

What does a zero dot product imply?

Vectors are orthogonal (perpendicular) and \theta=\frac{\pi}{2}

What are some other things to note about dot products?

• If v1=v2 then the it product = \left\vert v_1\right\vert^2

• Algebraic properties follow from the definition, such as

  • V1 . V2 = V2 . V1

  • V1 .(cV2)= (cV1).V2 for any scalar c

  • V1 . (V2+V3) = V1.V2 + V1.V3

Component of \mathbf{v}_1 in direction of \mathbf{v}_2

The component of a vector v1 in the direction of another vector v2 is the scalar quantity

|\mathbf{v}_1|\cos\theta = \frac{\mathbf{v}_1 \cdot \mathbf{v}_2}{|\mathbf{v}_2|}

Where \theta is the angle between the vectors.

Define the vector (cross) product.

\mathbf{v}_1 \times \mathbf{v}_2 = |\mathbf{v}_1|\,|\mathbf{v}_2|\sin\theta\,\hat{n}

Where \hat{n} is a unit vector perpendicular to both v1 and v2 such that {v1,v2,v3} form a right handed set, and \theta is the angle between the vectors.

Cross product in components for \vec{v}_1\times\vec{v}_2=|\vec{v}_1|\,|\vec{v}_2|\cos\theta

and the determinant form

\mathbf{v}_1\times\mathbf{v}_2=(\beta c-\gamma b,\;\gamma a-\alpha c,\;\alpha b-\beta a)

Think of it as the same way of calculating a determinant.

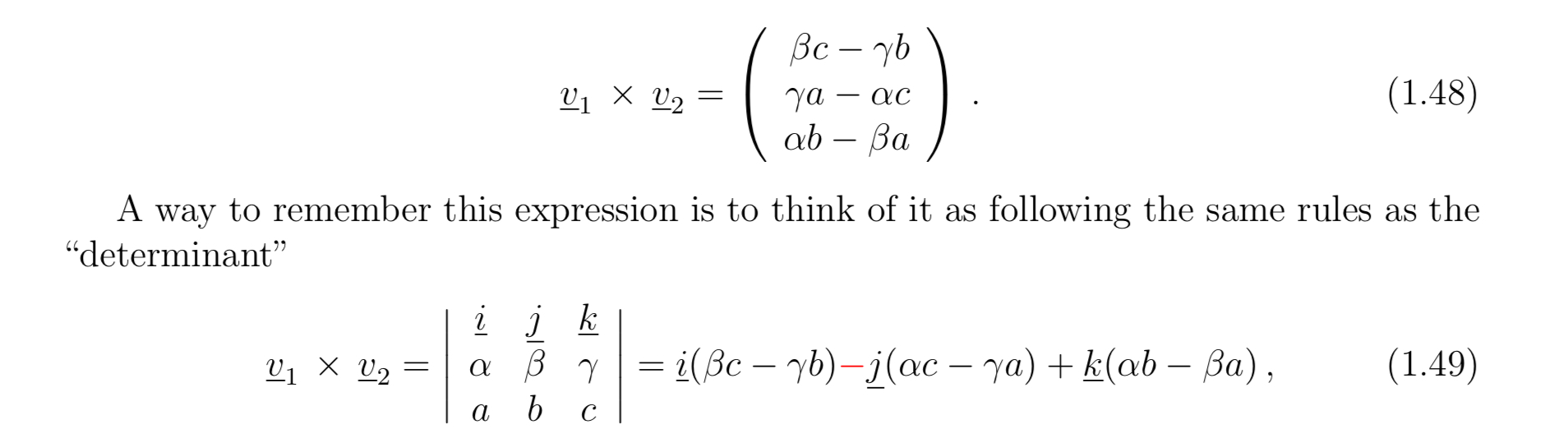
What is the cross product always perpendicular to?

The two ‘input vectors’

Does the cross product commute?

No

\vec{v}_1 \times \vec{v}_2 = -\,(\vec{v}_2 \times \vec{v}_1)

Is the cross product associative?

Not in general

(V1xV2)xV3 isn’t generally the same as V1x(V2xV3)

What are the algebraic properties of the vector cross product?

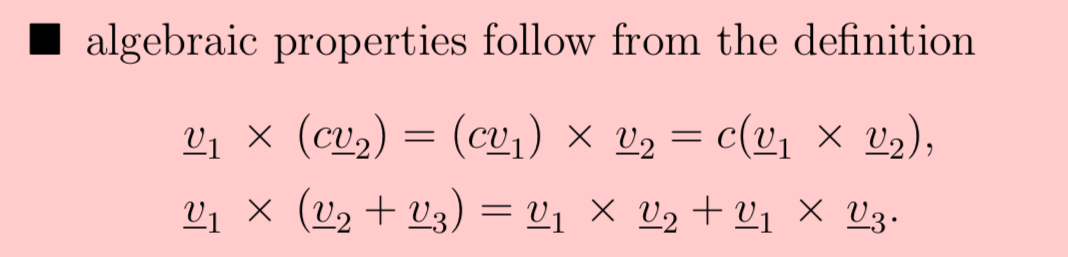
Basis-vector cross products.

\mathbf{i}\times\mathbf{j}=\mathbf{k},\; \mathbf{j}\times\mathbf{k}=\mathbf{i},\; \mathbf{k}\times\mathbf{i}=\mathbf{j}

Cross product when vectors are parallel.

\vec{v}_1 \times \vec{v}_2 = \vec{0}

Dot vs cross product roles.

Dot:

• The dot product of two vectors represents their similarity or how much they point in the same direction.

• Outputs a scalar

Cross:

• a new vector that is perpendicular to both original vectors. The magnitude of this new vector represents the area of the parallelogram formed by the two original vectors.

• vector output