CS 4110 Exam 1 Weber State

1-12 Module 1. 13-29 Module 2. 30-43 Module 3.

Suppose a closure is performed on a language L (in other words, the Kleene star L*). What is true of Λ in L*?

L* may have Λ

L* may have one or more Λ

L* always has Λ

L* never has Λ

L* always has Λ

Suppose an alphabet contains no words, and the language contains only the null string. What is true about the closure (i.e. the syntax using the Kleene star) of that language?

It is the empty set ∅ and infinite

It is the empty set ∅ and finite

It is the null string Λ and infinite

It is the null string Λ and finite

It is the null string Λ and finite

Suppose a language L = {a b c}. How many words of length 3 does L* have?
8

2

4

3

8
I think this question is bugged dawg. It a maka no sense. It should be 27 because 3 ^ 3 = 27

I think it’s supposed to ask how many 2 letter words. IE 2 ^ 3 = 8.

What is a recursive definition, as described in Chapter 3?

A function that calls itself.

A logical implication of the form "p implies q".

A rule 1 which explicitly uses rule 2. And a rule 2 which explicitly uses rule 1.

A base or basic starting point. Then a way to construct and place more words in the set from words already in the set. Finally stating no other elements are in the set.

A base or basic starting point. Then a way to construct and place more words in the set from words already in the set. Finally stating no other elements are in the set.

Which of the following operations are allowed in regular languages as defined in chapter 4?

Concatenation, closure (*), positive closure (+), or (|), and parenthesis grouping

Concatenation, closure(*), positive closure (+), or (+), ranges ([a..z]), zero or one (?), and parenthesis grouping

Concatenation, closure(*), and (&&), or (||), and parenthesis grouping

Concatenation, closure (*), or (+), and parentheses grouping

Concatenation, closure (*), or (+), and parentheses grouping.

Technically you can use C^+ (i.e., positive closure), but the book says it’s redundant because you can say the same with just the normal closure.

What is a good description for the following regular expression:

(a + b)*a(a + b)*b(a + b)* +

(a + b)*b(a + b)*a(a + b)*

This is not a valid regular expression

All words containing a's and b's of any number

All words containing at least one a and one b

All words containing two a's and two b's

All words containing at least one a and one b

What regular expression has an odd number of a's?

a(a+b)*a

b*ab*(aa)*b*

(a + b)*a(a+b)*a(a+b)*a(a+b)*

(ab+ba)*

b*ab*(aa)*b*

Which of the following symbols refers to an alphabet?

∅ (phi)

Σ (sigma)

Α (alpha)

Λ (lambda)

Σ (sigma)

What is a positive closure of a language, signified with the + superscript?

All permutations of words but Λ is included

Word permutations must occur only in lexicographical order

All permutations of words but Λ isn't included

Word permutations are limited to not allowing repeats

All permutations of words but Λ isn't included

For what reason does the textbook describe why recursive definitions are employed for languages?

To find the most efficient algorithm to accomplish a task

Languages are best thought as functions, and functions inherently allow recursion

To see that certain tasks are possible for a computer to do even if we do not know the best algorithms by which to do them

Because no other approach works for defining languages as they all have fundamental shortcomings

To see that certain tasks are possible for a computer to do even if we do not know the best algorithms by which to do them

What is true regarding regular languages and regular expressions?

All regular expressions haveregular languages associated with them

For all regular expressions, no regular language can be associated with them

Some, but not all, regular expressions can have regular languages associated with them

Regular expressions cannot be thought of in terms of regular languages, as they are two entirely different concepts

All regular expressions have regular languages associated with themf

What regular expression has an even number of a's and b's

(aa+bb)*

(a+b)*(a+b)*

(aa+ab+ba+bb)*

(ab)(a+b)*(ab)

(aa+bb)*

Suppose an alphabet of {a, b} and a finite automata (FA) is created to accept only all words whose second and third letter is bb. What is the minimum number of states this machine requires?

3

4

1

5

5

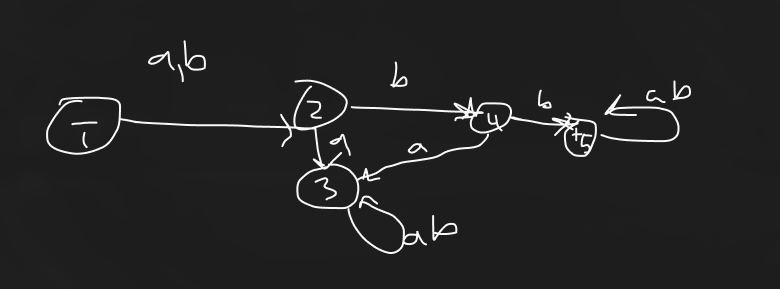
Suppose a finite automata (FA) is created with an alphabet of {a, b} such that the FA accepts only the two words aab and abb. What is the minimum number of states required?
8

5

6

16

5

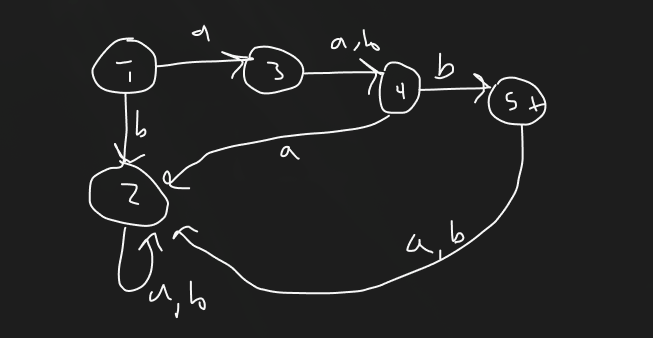
Can the transition graph shown  with four states be reduced to a graph with three states?
Yes

No

No

You can’t because if you did for say aa or bb for the first state, you could then end up with starting with aa and ending with bb, same is true for 2,3rd state. It will fundamentally break the TG.

What will the resulting language accept if the vandal swaps those two left edges coming out of the start state?

ab* + ba*

(a*+b*)*

b*+a*

(a+b)*

ab* + ba*

When using the bypass algorithm to remove states from a transition graph to turn it into a regular expression, can the resulting regular expression differ depending on the order in which states were removed?

False

True

True

You will have different regular expressions based off the order you do things but they will be fundamentally the same (ie doing the same thing).

Suppose FA1 has 2 states and FA2 has 3 states. If we want to create FA1 + FA2, what is the maximum number of states this new FA can have?

4

5

8

6

6 (2 + 3 + 1 new start state) — Correct answer: 6

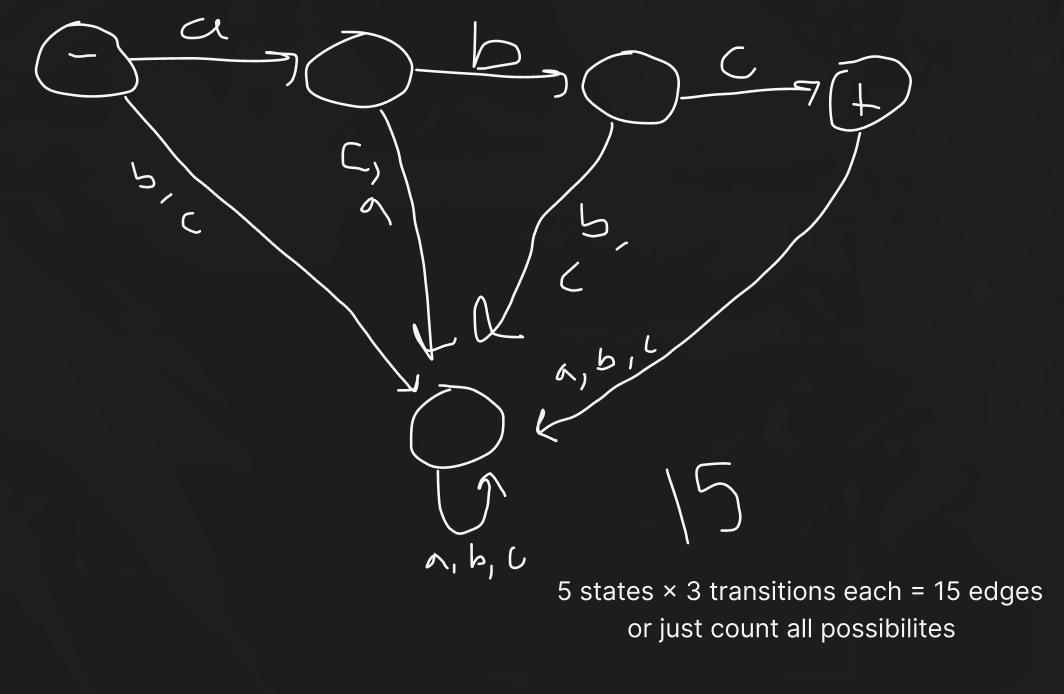
Suppose a finite automata (FA) is created with an alphabet of {a, b, c} such that the FA accepts a word abc. Further suppose that every edge has only one letter on it as a label, in other words, an isn’t labeled “a, b, c” but instead three edges are drawn with each having one letter on it. How many edges are required?

3

15

9

12

15

Suppose a finite automata (FA) is created with an alphabet of {a, b, c} such that the FA accepts one word of exactly three letters, such as cba. Further, the FA is written out as a transition table. How many transition table rows are needed (excluding the title/header row)?

3

12

5

4

5

Which of the following is correct regarding a transition graph (TG) differing from a finite automata (FA)?

A TG can have multiple start states while a FA can only have one start state

A TG can have can zero or more start states and zero or more final states while a FA can only have one start and one final state

None of the above

A TG can have multiple final states while a FA can only have final end state

A TG can have multiple start states while a FA can only have one start state

Suppose two finite automata FA1 and FA2 exist each representing two regular expressions called RE1 and RE2. The two regular expressions are concatenated to form (RE1)(RE2). How can the two FAs be concatenated?

It cannot be done, finite automata concatenation creates a transition graph.

Simply merge the final state of FA1 and the start state of FA2 together

Simply connect the final state of FA1 with the start state of FA2 together with enough edges for the alphabet letters

Run through scenarios. When the end state is reached of FA1 is reached, assume the possibilities allow either being in FA1's end state or FA2's start state. Then proceed further with this scenario potentially generating more scenarios.

Run through scenarios. When the end state is reached of FA1 is reached, assume the possibilities allow either being in FA1's end state or FA2's start state. Then proceed further with this scenario potentially generating more scenarios.

Suppose a finite automata (FA) is created with an alphabet of {a, b} such that the FA accepts a word aaa. Further suppose that every edge has only one letter on it as a label, in other words, an isn’t labeled “a, b” but instead two edges are drawn with one having an “a” and the other with a “b”. How many edges are required?

3

6

10

8

10

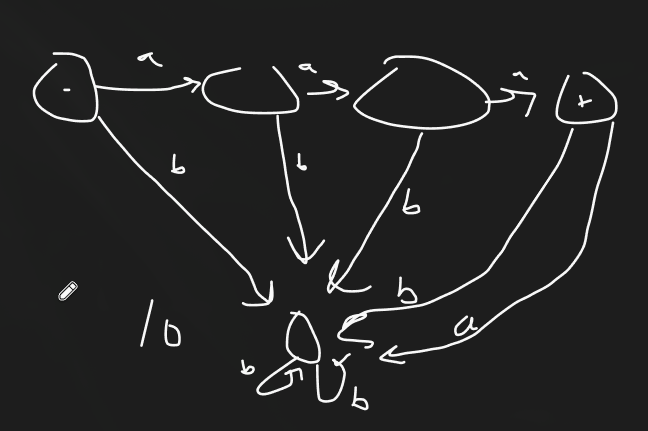
Suppose an alphabet of {a, b, c} and a finite automata (FA) is created to accept a word that starts with abc. What is the minimum number of states this machine requires?

1

5

4

6

5

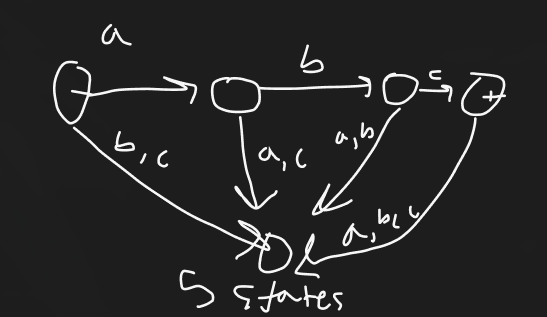
Which of the following are true regarding finite automata (FA)?

An FA can have only one start state and at zero or more final states

An FA can have at least one start state and zero or more final states

An FA can have at least one start state and at least one or more final states

An FA can have only one start state and one final state

An FA can have only one start state and at zero or more final states

hich of the following is NOT true regarding a transition graph's (TG) transition edges?

An edge can have the null string

An edge can have multiple letters

An edge can utilize the regular expression * (Kleene star) syntax to express the edge supports repeats of the input

A state can have multiple outgoing edges with the same transition label

An edge can utilize the regular expression * (Kleene star) syntax to express the edge supports repeats of the input

Which of the following are true regarding finite automata (FA)? (Assume the alphabet is {a, b}.)

The smallest FA has one state and no edges

The smallest FA has no states and no edges

The smallest FA has one state and two edges

The smallest FA has two states and four edges

The smallest FA has one state and two edges

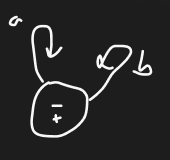
Suppose a finite automata (FA) is created with an alphabet of {a, b} such that the FA accepts all words that start with bb and ends with an aa. What is the minimum number of states this machine requires?

5

4

1

6

6

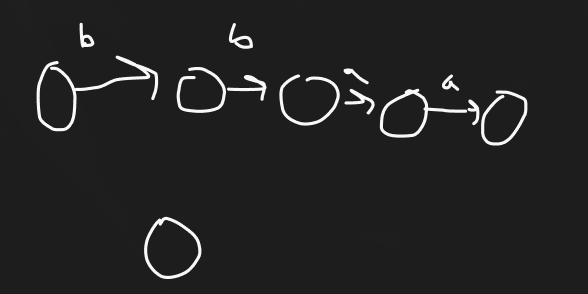
Suppose a finite automata called FA1 exists which is equivalent to a regular expression called RE1. The regular expression then has a Kleene star operation, making it (RE1)*. How can the FA1 stay equivalent?

It cannot be done, finite automata are in a different class of languages.

Create FA1 twice, then follow FA1's paths twice, each path starting at the start state. This creates a new FA.

Create a new start/final state with no incoming edges, and allow that to start from FA1's original start state. Then proceed checking all scnearios. When a final state is reached, treat the scenario as being in either the final state or the start state.

Append FA1 with another copy of FA1 by combining the final state for the first FA1 with the start state for the second FA1. That generates a new FA.

Create a new start/final state with no incoming edges, and allow that to start from FA1's original start state. Then proceed checking all scnearios. When a final state is reached, treat the scenario as being in either the final state or the start state.

How many z states would be created if we first listed all x and y scenarios?

8

5

12

9

9

3 states x 3 states.

Which of the following pump and stay in the language?

x = a, y = ba, z = a

x = a, y = aa, z = a

x = a, y = b, z = aa

x = aa, y = a, z = a

x = a, y = aa, z = a

aa makes it even to pump (repeat)

Which should be used to determine if aⁿbⁿcⁿ is non-regular?

The weaker form of the pumping lemma suffices because no choice of x y z will pump on y and stay in the language

The weaker form of the pumping lemma demonstrates the language is regular because an x y z will pump

The stronger form of the pumping lemma demonstrates the language is regular because of the length restriction

The stronger form of the pumping lemma suffices because an x y z choice does pump and stays in the language

The weaker form of the pumping lemma suffices because no choice of x y z will pump on y and stay in the language

Is it possible that when computing (L1 intersect L2') + (L1' intersect L2), that one of these two terms can accept no words while the other does? Or if one accepts no words the other will also always accept no words?

When one term has no words then the other term always has no words as well

One term can have no words but the other term can

One term can have no words but the other term can

Suppose a finite automata (FA) has N states. Using the blue paint method, what is the maximum number of iterations that could occur? Assume that painting the initial state blue does not count as an iteration, and that determining there are no edges left to travel also uses an iteration.

N-1

N

N+1

N-2

N

In a Venn Diagram (an A circle, a B circle, and an overlapping region of A and B), what is the space outside of A and B called?

(A or B)'

U

(A and B)'

A' and B'

(A and B)'

this turns into A’ or B’ , meaning not in a or b.

What is the complement of EVEN-EVEN?

EVEN-MIRROR

All words that have an odd number of a's or an odd number of b's

ODD-ODD

It cannot be complemented

All words that have an odd number of a's or an odd number of b's

What word is in the intersection of
L1 = even length strings
L2 = words have both an odd number of a's and an odd number of b's

bbbaa

ababab

aabbaa

abbbba

ababab

Even length and has odd a’s and b’s.

How should the Pumping Lemma be used on finite languages?

Only use the full/stronger form of the Pumping Lemma on finite languages

Words need only be pumped n times where n is the length of the largest word in the language

The same as before, the Pumping Lemma works on both finite and infinite languages

The Pumping Lemma shouldn't be used on finite languages as they are all regular

The Pumping Lemma shouldn't be used on finite languages as they are all regular

Just read black text in image.

What is an acceptable way to use the MyHill-Nerode Theorem to determine if aⁿbⁿ is nonregular?

Set x = a, y = ab, and z = b

The first class is Λ, the second class is ab, the third class is aabb, etc.

One class is all strings ending in b, the other class is all strings not ending in b

The strings a, aa, aaa, aaaa, etc., are all in different classes

The strings a, aa, aaa, aaaa, etc., are all in different classes

What is the complement of the language a*

b*

(a+b)*

a*(b)(a+b)*

b(a+b)*

b(a+b)*

What is one of De Morgan's laws?

Not (A and B) is the same as not A or not B

Not (A and B) is the same as the the complement of A and B

Not (A and B) is the same as the intersection of A and B

Not (A and B) is the same as not A and not B

Not (A and B) is the same as not A or not B

(A and B)’ = A’ V B’

The opposite of “and” is “or” & vice versa.

Why is the full/strong form of the Pumping Lemma sometimes used?

The full/strong form always determines if a language is non-regular

The full/strong form is more efficient at finding non-regular languages

The weaker form occasionally generates false positives, where it identifies a language as non-regular even though it really isn't

Some non-regular languages pump in the weaker form of the Pumping Lemma but won't in the full/strong form

Some non-regular languages pump in the weaker form of the Pumping Lemma but won't in the full/strong form

How can two regular languages L1 and L2 be checked for equivalence?

Use De Morgan's Laws to verify equivalence

Use the blue paint algorithm

Convert each to a regular expression and compare for similarities

None of the above

None of the above