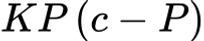Yellow Card Stuff to Know

sin(u)

cos(u)

cos(u)

-sin(u)

tan(u)

sec²(u)

cot(u)

-csc²(u)

sec(u)

sec(u)tan(u)

csc(u)

-csc(u)cot(u)

ln(u)

1/u

e^u

e^u

sin^-1(u)

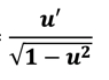
cos^-1(u)

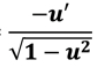
tan^-1(u)

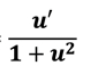
cot^-1(u)

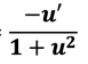
Limit from the left of f(x) as x → a

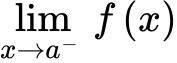
Limit from the right of f(x) as x → a

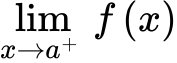
Definition of Continuity

1. f(a) is defined

2. Limit from left = limit from right

3. Overall limit = f(a)

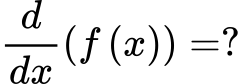
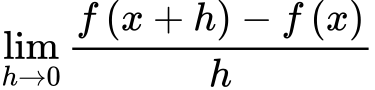
Chain rule

f’(u) * u’

Product Rule

uv’ + u’v

Quotient Rule

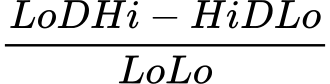
Intermediate Value Theorem

If f is continuous on the closed interval [a,b], where f(a) ≠ f(b) and k is a number between f(a) and f(b), then there is atleast one number c in (a, b) such that f(c) = k.

Mean Value Theorem

If f is continuous on the closed interval [a, b] and differentiable on the open interval (a, b), then there exists a number c such that:

L’Hopital’s Rule

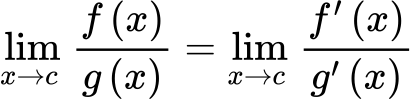
Critical Points

If f(x) is defined at x = c, then f(x) has a critical point at x = c if f’(c) = 0 OR f’(c) is undefined.

Global Minimum

f(c) < all other values of f(x)

Global Maximum

f(c) > all other values of f(x)

Extreme Value Theorem

If f is continuous on the closed interval [a, b], then f has both an absolute minimum value and absolute maximum in the interval.

F + G

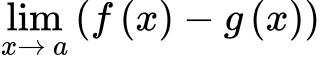
F - G

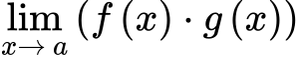
FG

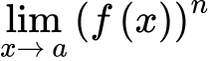
Fⁿ

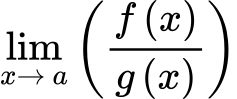
F/G

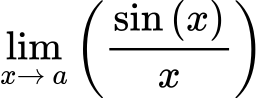
1

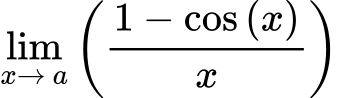
0

Fundamental Theorem of Calculus

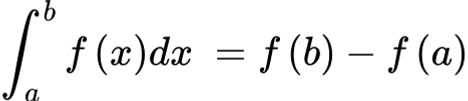
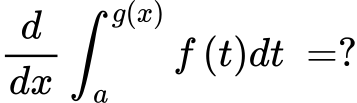
Corollary to FTC

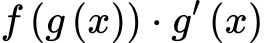
If continuous on [a, b] and x=c on (a, b) then…

(MVT/average value for integrals)

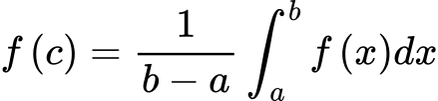
Disk Method

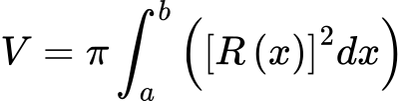
Washer Method

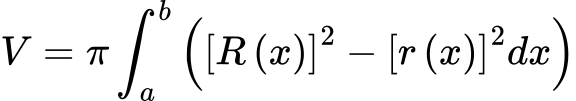
General volume equation

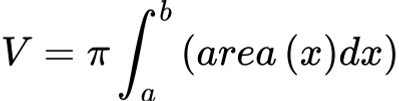
Arc Length (rectangular)

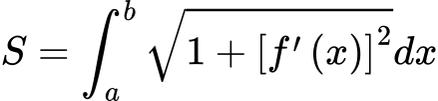
velocity

s’(t)

acceleration

s’’(t) = v’(t)

Speed (parametric and rectangular)

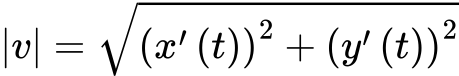
Displacement

Average velocity

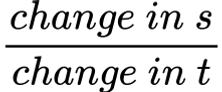
Euler’s Method

Integration By Parts

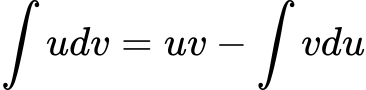
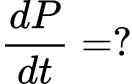
Logistics