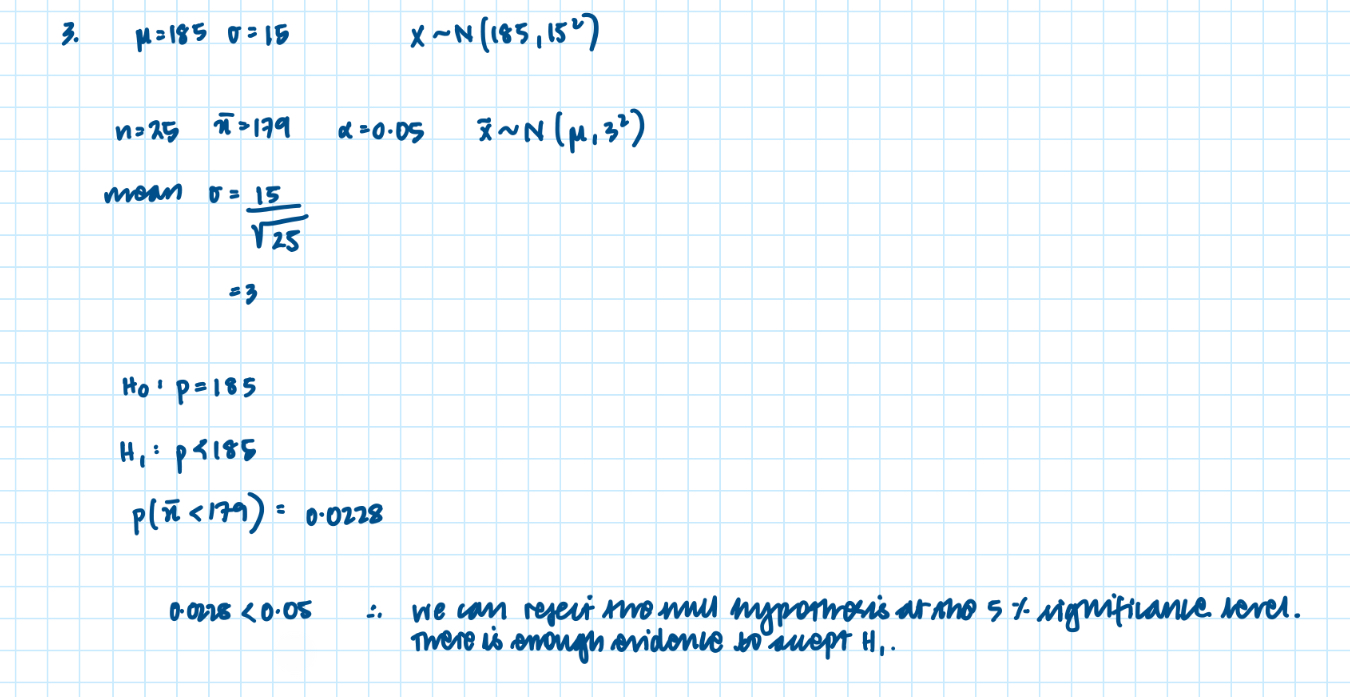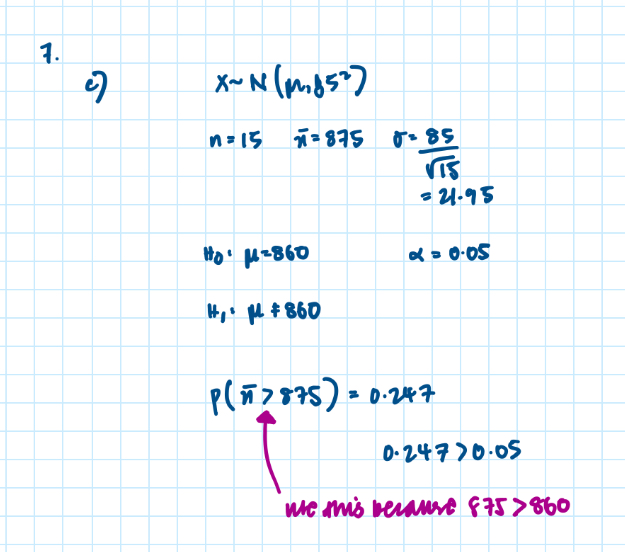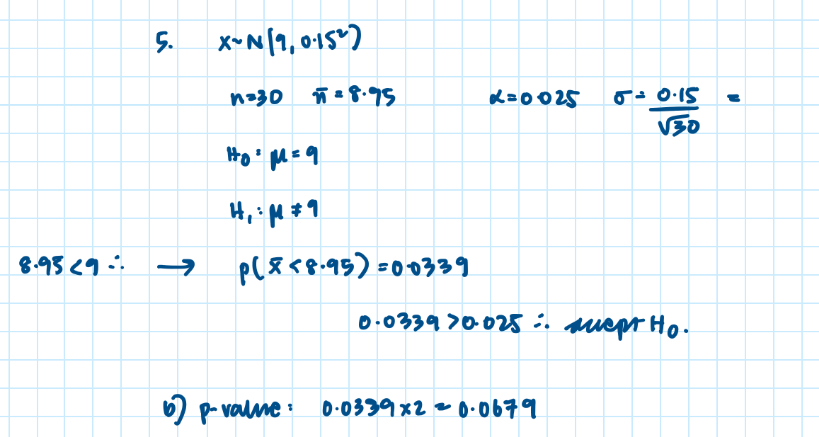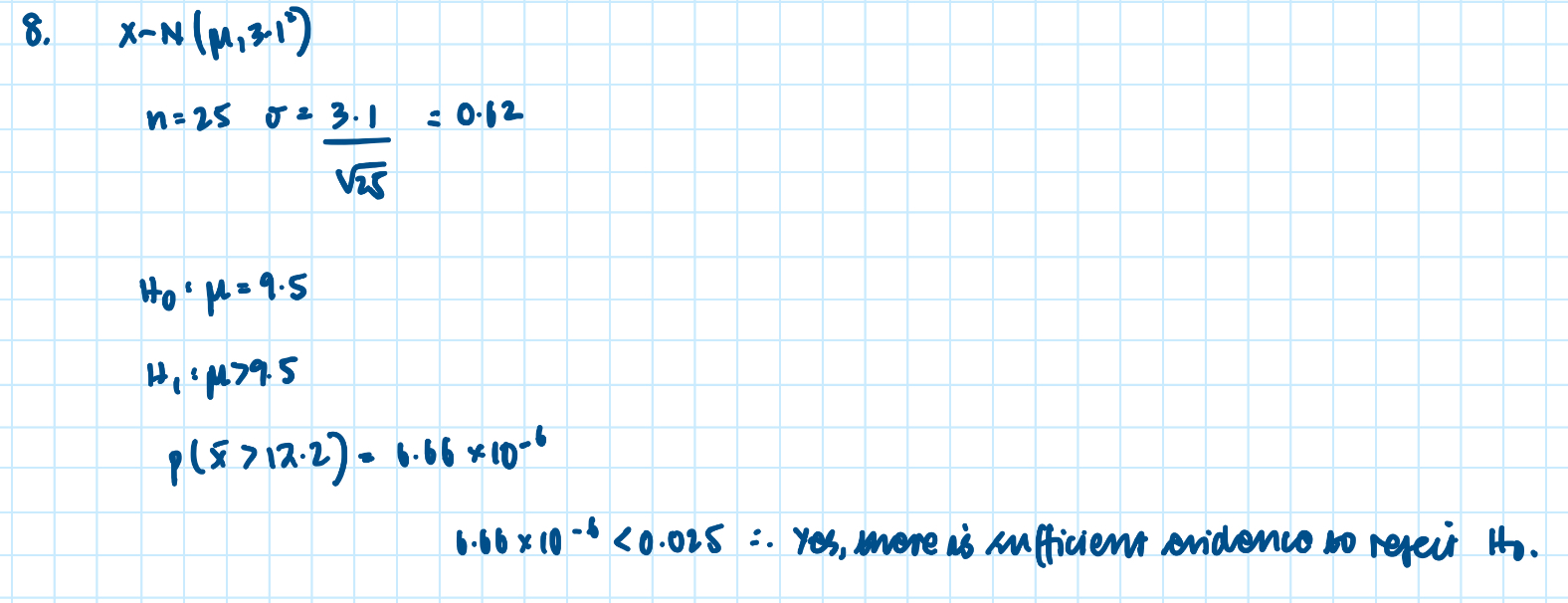The Normal Distribution:

Overview of the normal distribution:

A continuous random variable can take any one of infinitely many values. A continuous random variable has a continuous probability distribution. This can be shown as a curve on a graph.

The area under a continuous probability distribution is equal to 1.

A discrete random variable can only take certain distinct values.

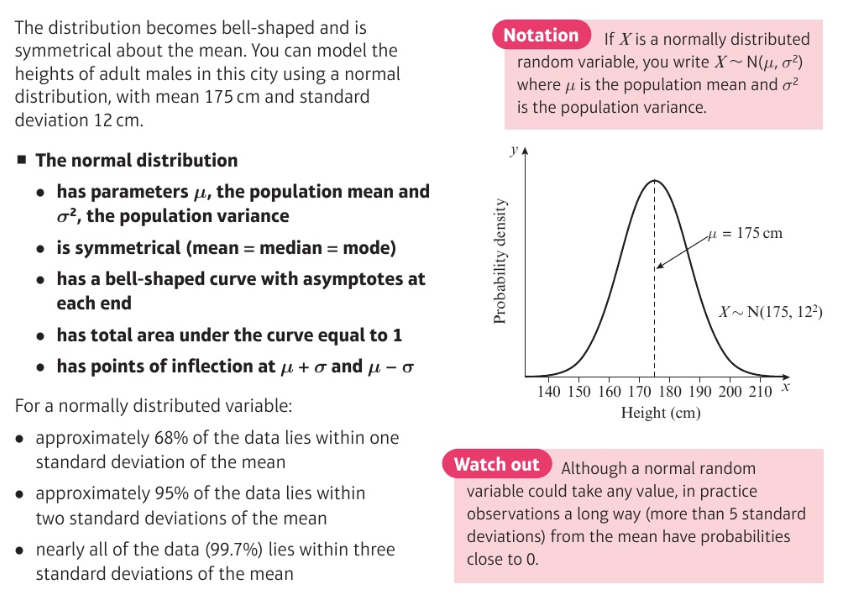
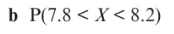
Finding probabilities using the normal distribution:

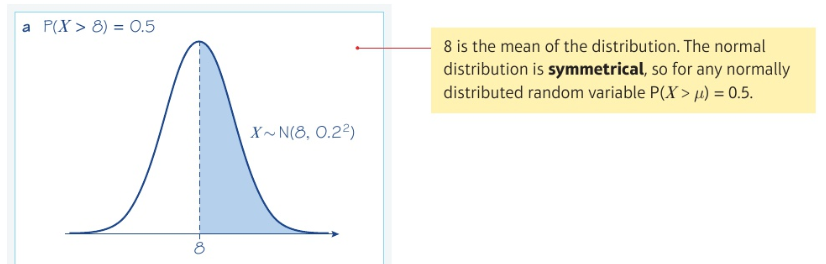
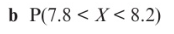
Finding probabilities using the normal distribution:

Using calculators to find probabilities for normal distributions:

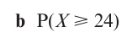
Using calculators to find probabilities for normal distributions:

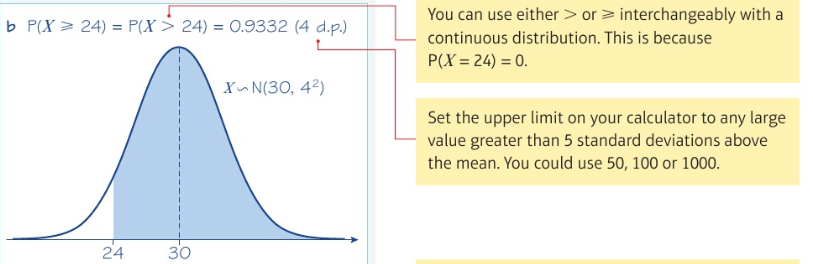
Using calculators to find probabilities for normal distributions:

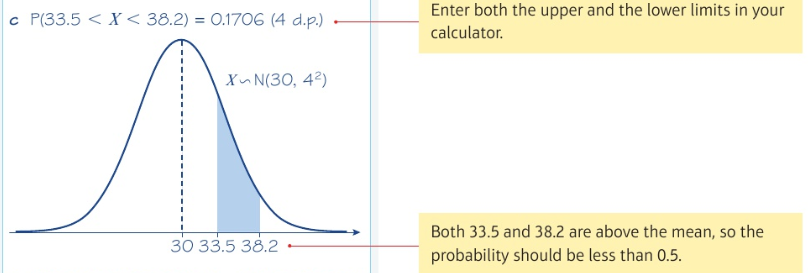
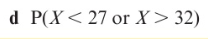
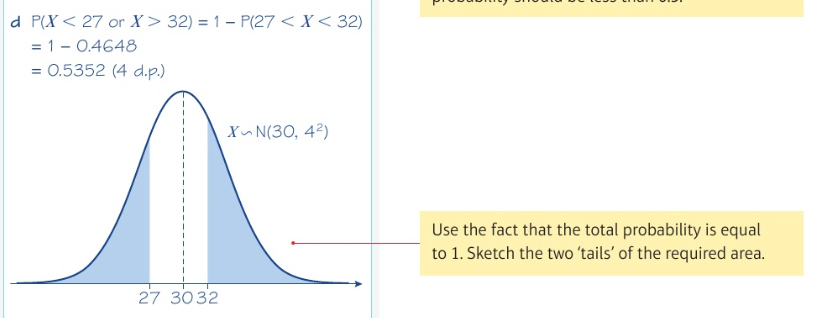
The inverse normal distribution function:

Examples of the inverse normal distribution function:

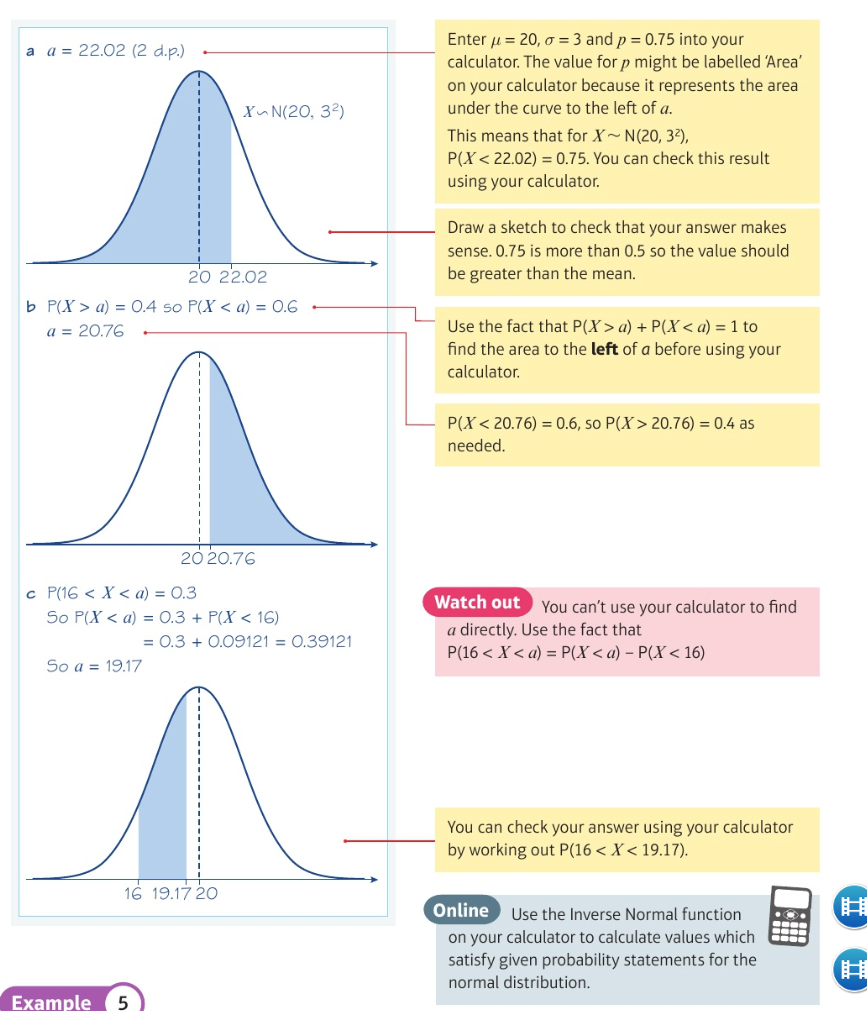
Examples of the inverse normal distribution function: (worded questions)

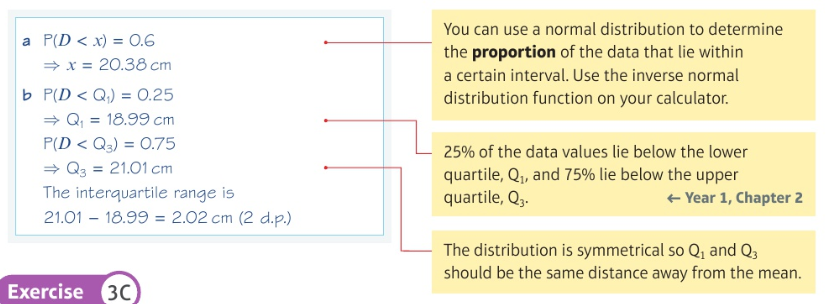
The standard normal distribution:

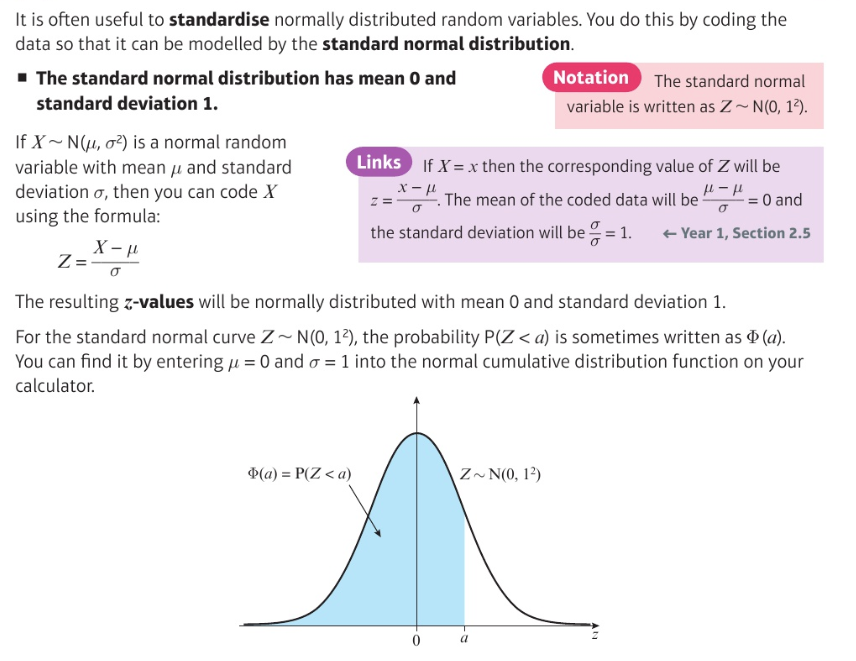
Using the standard normal distribution:

Using the standard normal distribution: (worded question)

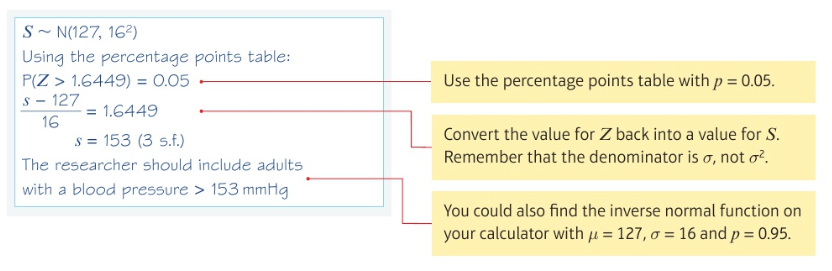
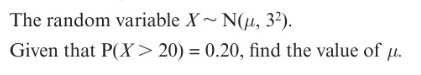
Finding an unknown mean or standard deviation for a normally distributed variable

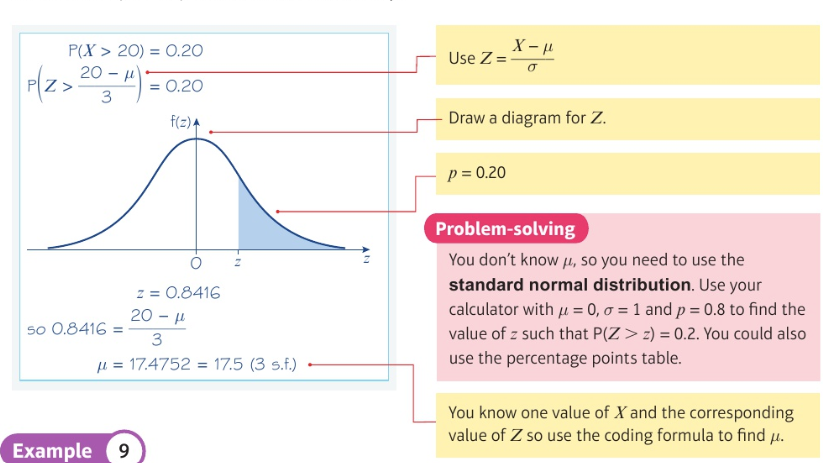
Finding an unknown mean or standard deviation for a normally distributed variable: (worded question)

b) X-N(50,5²)

let a be the 90th percentile

P(X<a)=0.9

a=56.4cm (1dp)

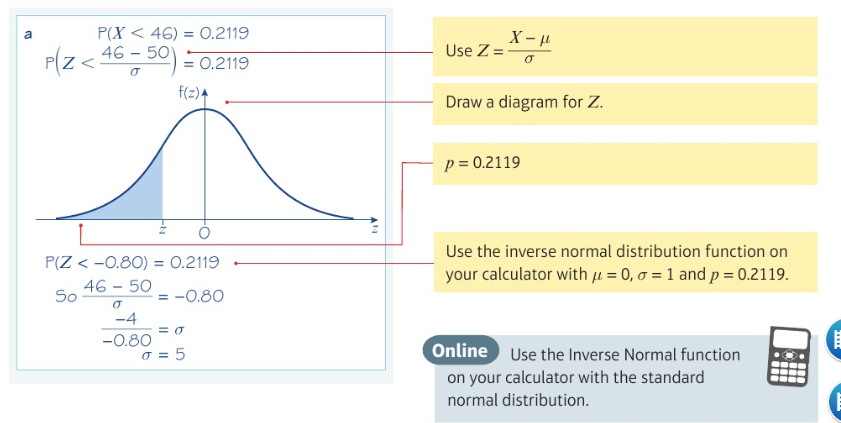
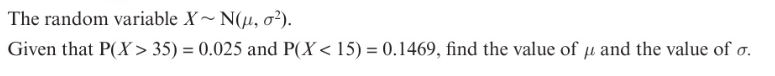
Using simultaneous questions to find the mean and standard deviation:

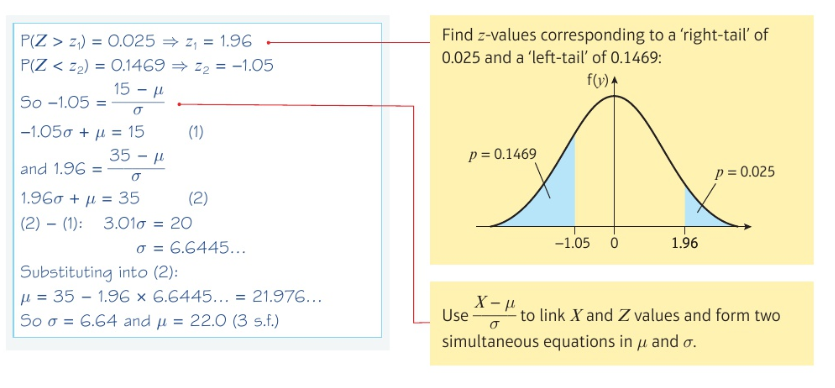
Approximating a binomial distribution:

Example of approximating a binomial distribution:

Applying a continuity correction:

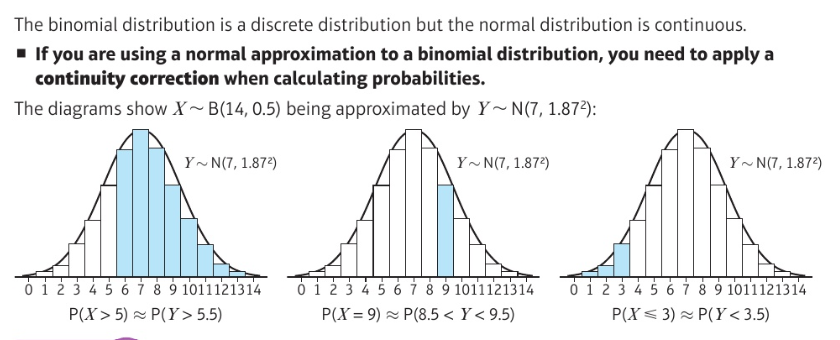
Example of applying a continuity correction:

Combining approximating a binomial and the continuity correction:

Hypothesis testing with the normal distribution:

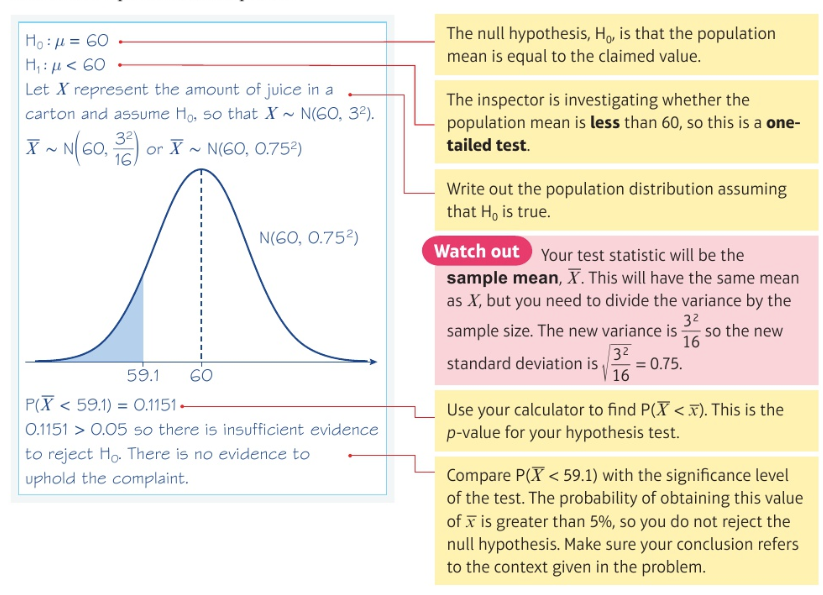
Example of hypothesis testing with the normal distribution:

Finding the critical region / critical value for a hypothesis test for the mean of a normal distribution:

Example of finding the critical region for a hypothesis test for the mean of a normal distribution: (part 1)

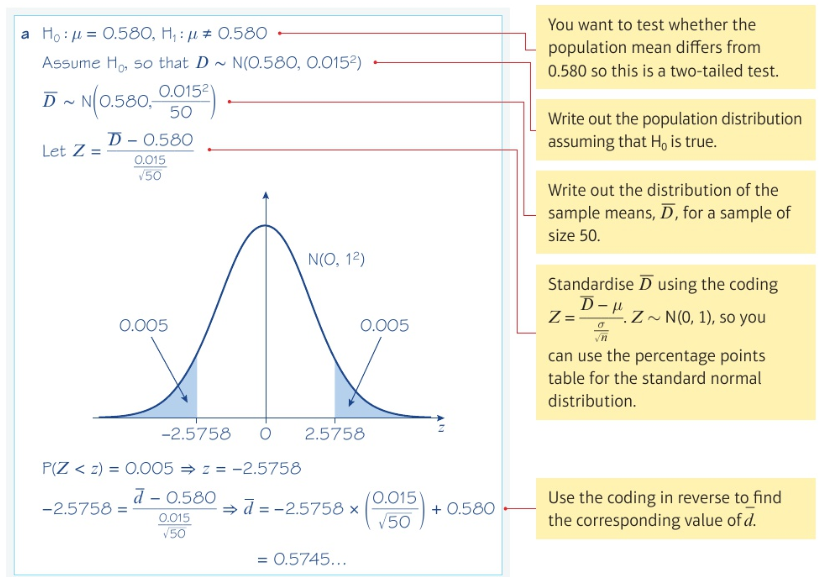
Example of finding the critical region for a hypothesis test for the mean of a normal distribution: (part 2)

Distribution of the sample mean: