1.3 Scalars & Vectors, 1.4 Errors & Uncertainties

Scalar

phys quantity w/ only magnitude

Vector

phys quantity w/ magnitude & direction

Scalar examples:
t__, d__, v__, de__, te__

time, distance, volume, density, temp

Vector examples:
v__, a__, d__, f__

velocity, acceleration, displacement, force

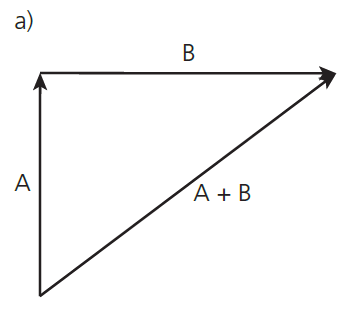
Vectors at right angles: find resultant using __

pythagoras

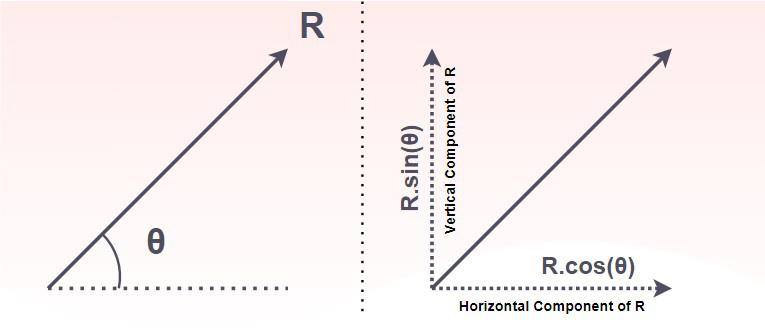
Vectors NOT at right angles
> Create dotted line that is p__ to bottom vector
> Use pythagoras

perpendicular

Random errors
> u__ error w/ measurement being a__/below true v__
> reduced via m__ measurements, then a__

uncontrollable, above, value, multiple, avg

Systematic errors
> from i__, reduced via s__ error

instrument, subtracting

Uncertainty (Δ)
2 types:
> A__
> P__

absolute, percentage

Uncertainty is usually either:
1. ± h__ of s__ division on instr. (usually when no possible e__)
2. ± 1 of smallest d__ - when possible error

half, smallest, error, division

If uncertainty can have random error (i.e. if given a range of values)
> Δ = ±(h__ of r__ of values)

half, range

Calculating uncertainties
+ or -: ADD __ uncertainties i.e. ΔP = ΔA + ΔB

absolute

Calculating uncertainties
x or /: ADD __ uncertainties i.e. Δ%P = Δ%A + Δ%B

percentage

Calculating uncertainties
Powers: x the __ uncertainty by p__, then by value to get Δ
e.g. if P = Aⁿ, ΔP = n(ΔA/A) x P

percentage, power

Uncertainty
+ or - uses a__ uncertainty thus constants d__ (do/don’t) matter

absolute, do

Uncertainty
x, /, power uses __ uncertainty thus constants d__ (do/don’t) matter

percentage, dont

Precision: s__/r__ of values of data

spread, range

Accuracy: how c__ the m__ values are to t__ values

close, measured, true