StemUp: OCR A A level Physics 5.1: Thermal physics

What is meant by two objects being in thermal equilibrium? (1)

Two objects are in thermal equilibrium when there is no net transfer of thermal energy between them.

How can two objects reach thermal equilibrium? (3)

- Place the two objects in contact, with one being hotter than the other.

- Thermal energy will flow from the hotter one into the colder one until they are the same temperature.

- There is no further transfer of thermal energy so the objects are in thermal equilibrium.

What is meant by temperature? (1)

This is a number which represents how hot an object is on some scale.

What is the thermodynamic scale of temperature? (2)

- This uses the triple point of water ,273.16K and absolute zero, as its fixed points.

- It is measured in Kelvin (K).

What is unique about the thermodynamic scale of temperature? (1)

It is an absolute scale of temperature that does not depend on the property of any particular substance to be measured.

What is the Celsius scale? (2)

- This marks the melting point of ice at 0 degrees and the boiling point of water at 100 degrees (under atmospheric pressure) and is used to measure temperature.

- It is not an absolute scale of temperature as it depends on the freezing and boiling points of water.

How is temperature converted from Celsius to Kelvin and vice versa? (2)

- A temperature increase of 1 Kelvin is equal to an increase of 1 Celsius but the starting point of the thermodynamic scale is 273.16 lower than Celsius.

- So to convert between the two use the equation: T(K) = T(°C) + 273.16

How are atoms and molecules arranged and spaced in a solid? (2)

- Atoms are closely packed together due to strong electrostatic forces of attraction between them.

- The atoms are ordered in a regular pattern called a lattice.

How do atoms and molecules move in a solid? (1)

The atoms and molecules have kinetic energy which allows them to vibrate around their fixed positions.

How are atoms and molecules arranged and spaced in a liquid? (2)

- The atoms and molecules have a greater separation than in a solid but are still close together.

- The electrostatic forces are weaker than in solids so they are spaced less regularly.

How do atoms and molecules move in a liquid? (1)

Atoms and molecules are free to move with a fixed volume and they can take the shape of any container.

How are atoms and molecules arranged and spaced in a gas? (2)

- The electrostatic forces between atoms and molecules are at a minimum so they are completely spread out.

- There is no regular spacing for particles in a gas.

How do atoms and molecules move in a gas? (1)

The atoms and molecules have their maximum kinetic energy so they move freely and rapidly, colliding with each other.

What does the kinetic theory for solids show? (3)

Due to there being very strong intermolecular forces :-

- Solids have a fixed shape and volume (some can be deformed using forces).

-Difficult to compress.

- Have a higher density than air and gas.

What does the kinetic theory for liquids show? (3)

Due to them having weaker intermolecular forces than solids :-

- Do not have a fixed shape so can flow in any container but do have a fixed volume.

- Are difficult to compress.

- Have lower densities than water but higher densities than ice.

What does the kinetic theory for gases show? (3)

Due to them having negligible intermolecular forces :-

- Do not have a fixed shape or volume.

- Can be compressed.

- Have the lowest density compared to liquids and solids.

What is meant by Brownian motion? (1)

This is when the molecules of a gas travel in random directions with random values of velocity.

How can Brownian motion be represented with smoke? (2)

- Smoke particles are visible under a microscope.

- They exhibit Brownian motion because of their collisions with the molecules in air, which result in a transfer of momentum in random ways.

What is meant by the internal energy of a substance? (1)

This is defined as the sum of the randomly distributed potential and kinetic energies of the molecules that make up the substance.

What is meant by absolute zero (0K)? (1)

This is the lowest possible temperature and molecules stop moving completely due to there being no kinetic energy.

What happens to the internal energy of a substance at absolute zero? (1)

The substance has a minimal internal energy which is all due to the electrostatic potential energy as the molecules do not have any kinetic energy.

What happens to the internal energy of a substance at the temperature increases? (1)

The kinetic energy of the molecules increases whilst the potential energy stays the same so the internal energy will increase as it is the sum of the kinetic and potential energies.

What happens to the internal energy of a substance as it changes phase (from solid to liquid to gas)? (1)

The potential energy of the molecules increases whilst the kinetic energy stays the same so the internal energy will increase as it is the sum of the kinetic and potential energies.

What happens to the temperature of a substance as it changes phase (from solid to liquid to gas)? (1)

The temperature will remain constant as thermal energy is being transferred to overcome electrostatic bonds between molecules, not raising the temperature.

What is meant by the specific heat capacity (c) of a substance? (1)

The specific heat capacity is defined as the energy required per unit mass to raise the temperature of a substance by 1K or 1 degree Celsius. It is unique for each substance.

What is the equation for specific heat capacity? (1)

This is given by: E = mc∆θ​

Where E is the energy (J) supplied to the substance, m is the mass (kg) of the substance, c is the specific heat capacity (Jkg⁻¹) and ∆θ is the change in temperature of the substance.

What are the S.I. units for specific heat capacity? (1)

They are Jkg⁻¹

How can an electrical heater be used to find the specific heat capacity of a substance? (4)

- Heat a known mass of substance with a heater with a known power over a long period of time.

- The energy supplied by the heater (W = IVt) is equal to the energy supplied to the substance (E = mc∆θ​) so the two can be equated: IVt = E = mc∆θ​.

- Rearrange for specific heat capacity (c) to find: c = IVt / m∆θ.

- ​Use an insulator to reduce heat transfer to the environment and increase accuracy of this method.

What is the specific latent heat of fusion (L_f)? (1)

This is the energy required per unit mass to change the phase of a substance from a solid into a liquid and vice versa. It is unique for each substance.

What is the specific latent heat of vaporisation (L_v)? (1)

This is the energy required per unit mass to change the phase of a substance from a liquid into a gas and vice versa. It is unique for each substance.

What is the equation for specific latent heat? (1)

This is given by: E = mL

Where E is the energy (J) transferred to the substance, m is the mass (kg) of the substance and L is the specific latent heat of the substance (Jkg⁻¹)

What are the S.I. units for specific latent heat? (1)

They are Jkg⁻¹

How can an electrical heater be used to find the specific latent heat of a substance? (4)

- Heat a known mass of substance with a heater with a known power, the period of time where the temperature is constant (changing phase) is used in the following calculations.

- The energy supplied by the heater (W = IVt) is equal to the energy supplied to the substance (E = mL) so the two can be equated: IVt = mL​

- Rearrange for specific latent heat (L) to find: c = IVt / m

- Use an insulator to reduce heat transfer to the environment and increase accuracy of this method.

How can the amount of substance be measured? (1)

This can be measured using the S.I. unit the mole. One mole is the amount of substance containing 6.02 x 10^23 atoms or molecules.

What is the Avogadro constant (N_A)? (1)

This is equal to 6.02 x 10^23 mol^-1.

How is the number of molecules in a substance found? (1)

The number of moles (n) is found using n = m / M​

Where m is the mass (kg) of the substance and M is the molar mass (kg) of the substance (mass of one mole).

What does the kinetic theory of gases describe? (1)

It describes how particles within an ideal gas behave.

What are the assumptions used to model a gas as an ideal gas? (5)

- The gas contains many atoms that undergo Brownian motion (random, rapid motion).

- The volume of the gas atoms is negligible compared to the total volume of the gas.

- All collisions between atoms and between an atom and the wall are perfectly elastic collisions.

- The time taken for a collision is negligible compared to the time between collisions.

- The electrostatic forces between atoms is negligible except for when the atoms are colliding.

How do ideal gas atoms move? (1)

The atoms undergo Brownian motion (random, rapid motion).

How does the volume of ideal gas atoms compare to the volume of the gas? (1)

The volume of the gas atoms is negligible compared to the total volume of the gas.

How are collisions involving atoms in an ideal gas modelled? (2)

- All collisions between atoms and between an atom and the wall are perfectly elastic collisions.

- The time taken for a collision is negligible compared to the time between collisions.

How are electrostatic forces between ideal gas atoms modelled? (1)

The electrostatic forces between atoms is negligible except for when the atoms are colliding.

How does the ideal gas model explain pressure? (4)

- The collisions between ideal gas atoms and the wall are perfectly elastic so the speed stays constant.

The change in momentum is given by mv -(-mv) = 2mv for a single ideal gas atom.

- From Newton's second law, F = ∆p \ ∆t so the force exerted on the wall by an ideal gas atom is F = 2mv / t where t is the time of the collision. This is the pressure on the wall.

- The total pressure on the wall is equal to the sum of the force of each collision between atoms in the gas and the wall, and the area of the wall.

What is Boyle's law for an ideal gas? (1)

Boyle's law states that for a mass of an ideal gas at a constant temperature, the pressure is inversely proportional to the volume. So P ∝ 1 /V

What is Charles' law for an ideal gas? (1)

Charles' law states that for a fixed mass of gas at a constant volume, the pressure is proportional to temperature. so p ∝ T

What is the equation of state for an ideal gas? (1)

This is given by pV = nRT​

Where p is the pressure of the gas (Pa), V is the volume the gas is contained in (m^3), n is the number of moles of gas (mol), R is the molar gas constant (8.31 Jmol^-1K^-1), and T is the temperature (K) of the gas.

How is the root mean square speed (c) for a gas found? (2)

- This is found by summing al the individual velocities of the molecules in the ideal gas and dividing by N (total number of molecules) to find the mean square speed.

- The square root of this is taken to find the root mean square speed.

How can the root mean square speed be used to find the pressure of an ideal gas at a microscopic level? (1)

By using this formula: pV = 1 / 3 Nmc^2

Where p is the pressure (Pa), V is the volume (m^3), N is the number of molecules or atoms in the ideal gas, m is the mass (kg) of a single molecule or atoms and c^2 is the root mean square speed (ms^-1)

What is the Boltzmann constant (k)? (1)

This is equal to the molar gas constant (R) divided by Avogadro's constant: k = R / N_A it has a value of 1.38 X 10^23JK^-1

How can the ideal gas equation be written in terms of the Boltzmann constant (k)? (2)

- The equation pV = nRT can be written as pV = NRT / N_A as n is the number of moles found by N / N_A where N is the number of molecules in the ideal gas.

- As the Boltzmann constant is equal to N / N_A the ideal gas equation can be rewritten to be: pV = NkT​

What is the relation between the mean kinetic energy of a gas and the temperature of a gas? (1)

The kinetic energy of gas molecules is proportional to the temperature (in Kelvin). At a given temperature, every gas molecule in a specific substance has the same kinetic energy.

How can an equation for the mean kinetic energy of a gas be derived? (3)

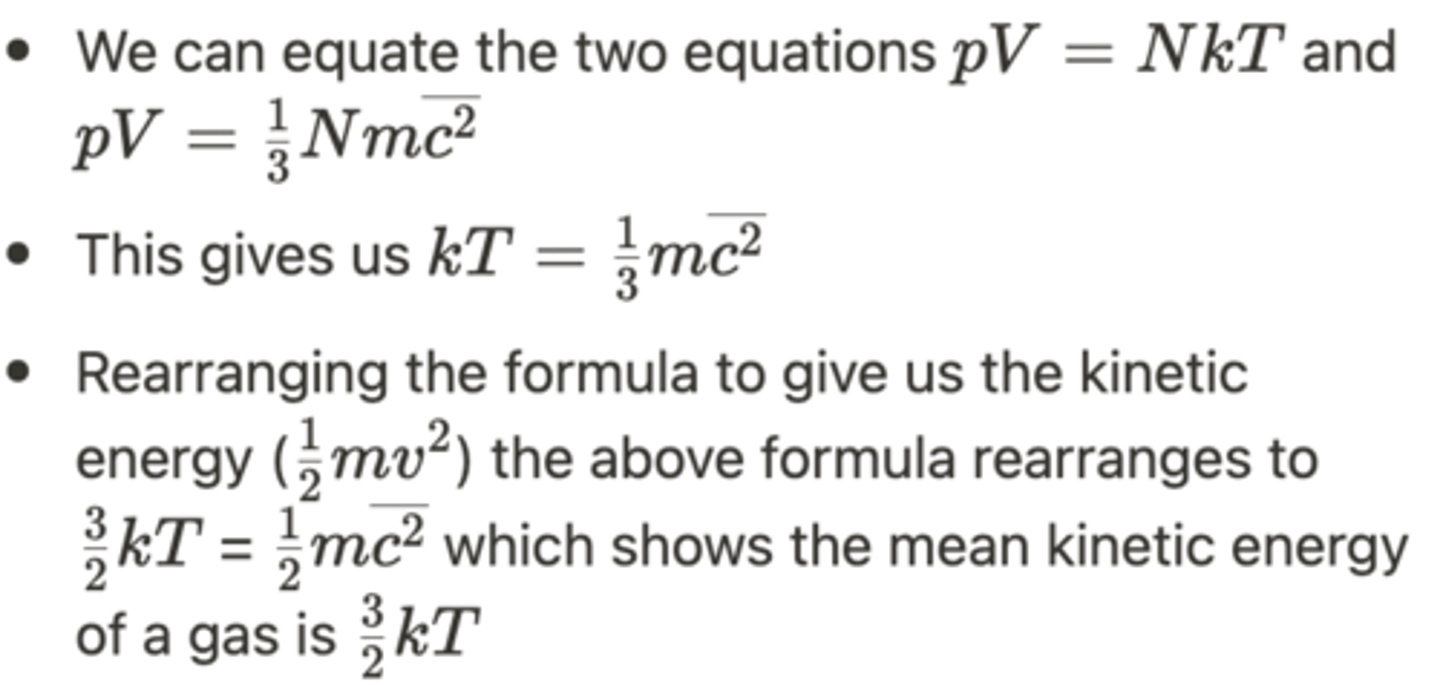
What is the internal energy of an ideal gas? (2)

- The internal energy is equal to the sum of the kinetic and potential energies of the atoms/molecules in the ideal gas.

- However in an ideal gas there are no electrostatic forces between atoms so there is no potential energy and the internal energy is equal to the sum of kinetic energies of the atoms/molecules.