Close Packing Spheres and Cubic structures

Flash cards for lecture 2 of Sold States and Diffraction

Why do we use close packing spheres

-Much like atoms these spheres cannot be packed into a box without leaving air gaps, but can be packed in a way which minimises the air gaps between them.

What are the two most common ways of packing

Cubic Close Packing (ABC)

Hexagonal Close Packing (ABA)

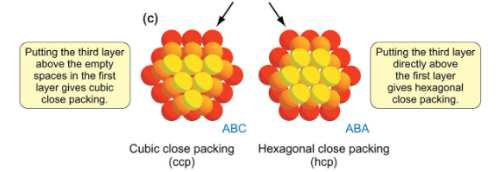
What does coordination number refer too, and describe how many CCP and HCP have

Coordination number, is  the number of nearest neighbours an atom has. Cubic and hexagonal close-packed structures both have coordination numbers of 12. 

There are 6 in the same layer then 3 above and below.

Why is CCP the only close packed cubic cell

All other cubic cells have much lower coordination numbers so aren’t consider and close packed.

Name the three most common cubic structures and give their coordination number

-Face centred cubic (another name for cubic close packed), coord number = 12

-Body centred cubic, coord number = 8

-Primitive cubic, coord number = 6

Describe BCC metals and give an example of one.

-BCC metals are often harder and less malleable than close-packed metals.

-This is due to, when a metal is deformed the atomic plates must slip over each other- this is more difficult for BCC structures

-An example of BCC metals are, Barium and Chromium

Define a lattice

A lattice is a network of identical points that has the translational symmetry of a structure.

Define a unit cell

Smallest possible repeating unit for the lattice structure.

How to calculate the packing efficiency of lattice points in a unit cell.

(For a cube, of side length a, face diagonal length b, and body diagonal, c)

-First take the unit cell, should be a cube with multiple spheres and sections of spheres.

-Then we find the volume of the entire unit cell.

-Next we count the number of atoms (parts of atoms) in the unit cell, and find the volume of them.

-Finally, packing efficiency = volume of atoms / volume of the cell

What’s the highest value for packing efficiency

74% from FCC

What are the packing efficiencies of the 3 most common cubic

FCC = 74%

BCC = 68%

PC = 52%

How do we calculate mass of a unit cell

Mass of unit cell = (number of atoms x Relative atomic mass) / Avogadro's Constant