Government & Business Econ 421 Douglass Davis Final

Identify two reasons that a dominant firm might enjoy lower costs than members of a competitive fringe.

Do these are these advantages tend to be long lived? Explain briefly.

Reasons:

a) Economies of Scale

b) Learning Curve

c) Superior Product

Longevity: These are temporary and will dissipate with significant entry.

Optimization for the dominant firm. Complete the two panel chart at the top of the next page to identify:

i) The effects of competitive fringe on demand curve for the dominant firm

ii) Marginal revenue for the dominant firm

iii) Profit maximizing quantity, price and profit for the dominant firm

iv) Fringe supply under profit maximization

LOOK

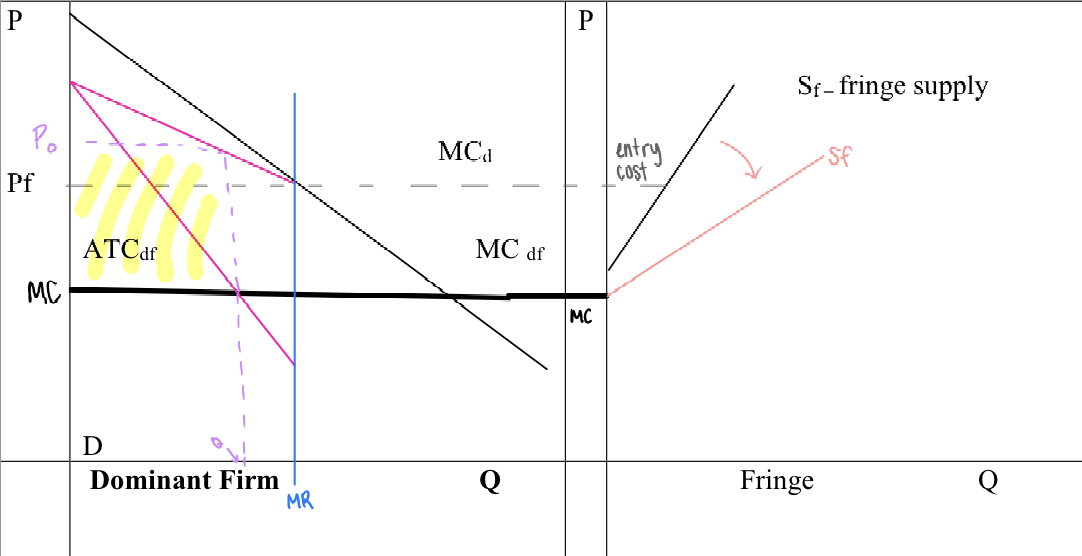
Limit Pricing Behavior The two panel graph below repeats the above graph. Use it to identify the limit pricing solution for the dominant firm. In you graph, be certain to show:

i) The quantity, price and profit for the dominant firm under limit pricing

ii) Fringe supply under limit pricing.

iii) If you’ve drawn your graph correctly, static profits under limit pricing are lower than under profit maximization. What dynamic consideration might make limit pricing an optimal solution for the firm?

LOOK

Give three examples of dominant firms who have let their position erode over time.

1. U.S Steel

2. Reynolds

3. Xerox

Give two examples of dominant firms who have engaged in limit pricing to preclude entry.

1. Alcoa (1945)

2. Dupont - cellophane (1924-1927)

According to contestability theory, under certain conditions the number of firms in a market is unimportant.

Identify three critical conditions:

1. No exit barriers

2. Entry is complete

3. No entry barriers

If a market satisfies the contestability assumptions, what price is predicted?

How many firms are necessary to be servicing a market to yield competitive prices?

Price Prediction: Price will equal average cost Pc = LRAC

How many firms: 1

In what theoretical context is the Demsetz Hypothesis proposed?

Challenges SCP—says high profits and concentration can come from efficiency, not monopoly power. (tool for monopoly regulation)

Briefly, what is the proposed policy? (Demsetz Hypothesis)

Given natural monopoly, auction off the right to the monopolist

Factors enhancing the magnitude of network effects on market structure.

1. Complementary, compatibility

2. Consumption externalities

3. Switching costs and lock-in

4. Economies of Scale

Identify two other industries where network effects similarly preclude effective competition.

1. Social Media

2. Online Marketplaces

The Cournot Duopoly — Joint Maximizing Outcome

a: P if Q=0

c: MC

Q= (a-c)/2 —> Each firm: q = Q/2

P = 190-Q = 100

Profit per firm: π = (P-MC)q

Total profit: 2π

Point on graph: (Q,P)

The Cournot Duopoly — Competitive Outcome

P = MC = 10

Solve for Q: 10 = 190-Q = 180

Since P=MC —> Profit = (P-MC)Q = 0

Point on graph: (Q,P)

The Cournot Duopoly — Cournot Equilibrium Outcome

P = 190 - (q1 + q2)

π1 = (P-MC)q1

Find derivative (q1): 180-2q1-q2 = 0 —> 90-.5q1 —> symmetry makes = q2

Substitute: q1 = 90-.5(90-.5q1) = 90-45+.25q1 —> .75q1 = 45 —> q1=60

Total Q = 2(q1)

Total P = 190-(Q)

Profit per firm: π = (P-MC)q1

Point on graph: (120,70)

Compare the combined equilibrium profits for firms A and B pre-merger and post-merger.

Pre:

Firm A = 1,200

Firm B = 1,200

Total AB = 2,400

Post: 1,600 —> MERGER IS NOT PROFITABLE

Bertrand Competition: Suppose that two firms each have constant average variable (and marginal) costs of $50 per unit. Market demand is given by Q=100-P and the minimum price increment is $1

a. Find the Bertrand equilibrium price, quantities and profits.

Demand: Q=100-P —> Q=100-50=50 —> each firm: 50/2=25

πPerUnit=P-MC —> 50-50=0

πPerFirm=(P-MC)Q —> (50-50)25=0

Bertrand Competition: How would your answer change in (a) if there were three firms?

Total Q demanded: 50

Each firm gets: 50/3=16.67

πPerFirm: still 0

Bertrand Competition: What assumption about the homogenous product Bertrand model is empirically most questionable?

Identify a way that you might change the way that you model static Bertrand interactions to correct this assumption.

How does this alternative affect the Bertrand equilibrium prediction?

Questionable Assumption: All firms sell homogeneous products and have no capacity constraints

A change: Assume product differentiation or include capacity constraints

Effect on Bertrand Equilibrium Prediction: Prices stay above MC and firms earn positive profits, even with multiple competitors

Capacity Constrained Price Competition: Illustrate supply and demand for this market in the coordinate axes below.

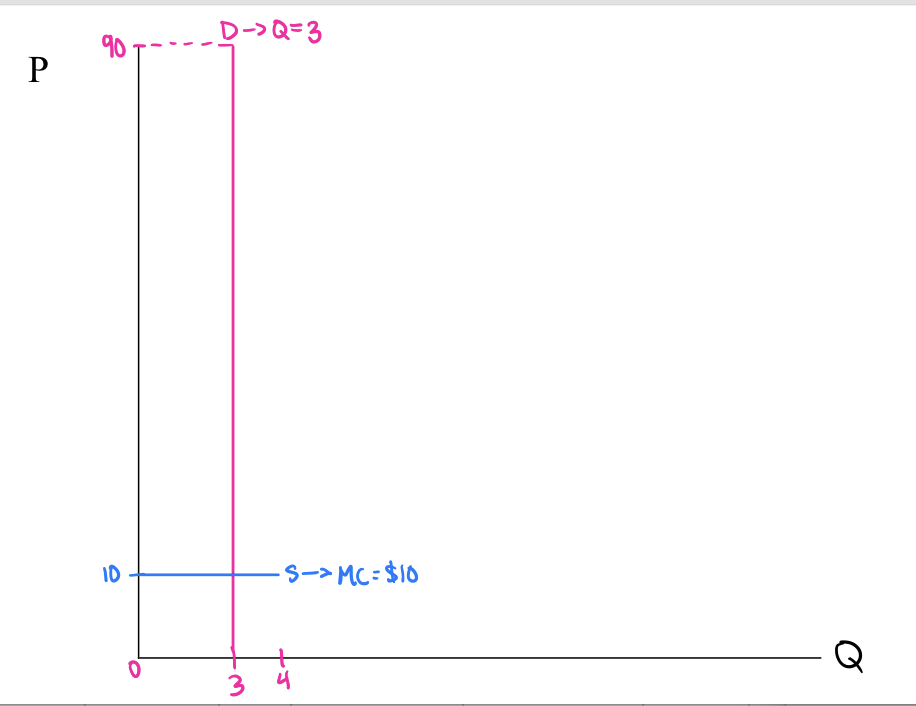
Capacity Constrained Price Competition: 2 sellers each of whom produce 2 units. Cost per unit is $10. There are 3 buyers in the market that value the product at $90. What is the joint maximizing price for the sellers? What do they each earn in this case?

Total revenue in market = $270

Total joint profit = (270-30) = $240

Profit per seller: 240/2 = $120

Capacity Constrained Price Competition: Is the joint maximizing price equilibrium for this market? Why or why not?

No. Each seller has incentive to undercut the other to sell more units

Capacity Constrained Price Competition: What is the minimum price that either of the two sellers would post? Why does this price exceed the competitive price of $10 per unit?

Residual demand 90-10×1 = 80

(Pmin-10)2 = 80

Pmin = 50

If they set prices too low they will exhaust their capacity

The effects of repetition on Oligopoly:

• If both Cooperate, each seller earns $500 per period

• If both Defect, each seller earns $200 per period

• If one Cooperates and the other Defects, the defector earns $700 per period while the defected upon earns $100.

Illustrate this game in normal form in the table below. Identify the Nash equilibrium for the game.

The effects of repetition on Oligopoly:

Suppose the game is repeated 432 times and then stopped. Both players know that the game will continue for exactly 432 periods. As a theoretical matter, may the CC outcome be a Nash equilibrium for this repeated game? Explain.

No, because cooperation unravels from the last stage to the front

The effects of repetition on Oligopoly:

Suppose that the game is repeated indefinitely.

What sort of strategy might support cooperation in the repeated game

A trigger strategy: Both players cooperate unless one defects, then they both defect forever as punishment.

The effects of repetition on Oligopoly:

Use the Friedman Coefficient to identify the minimum discount factor necessary to support cooperation as an equilibrium for this game.

Identify values for the variables C, D, and P in the above

Now find F

C=500 D=700 P=200

F: F= (D-C)/(D-P) —> (700-500)/(700-200)

F = .4

The effects of repetition on Oligopoly:

What does your F mean?

What does it mean about the interest rate?

F=.4 means players must value future profits enough (at least 40% of current profits) to be sustainable

r<(1-F)/F —> (1-.4)/.4 = 1.5 —> r<150%

Interpretation: If the interest rate is below 150%, cooperation can be sustained

Factors Affecting Tacit Collusion:

Identify two factors that identify the necessary market power

1) Inelastic demand

2) Barriers to entry

Factors Affecting Tacit Collusion:

Identify four factors that reduce the costs of collusive agreements

1) Few firms

2) infrequent sales

3) static market

4) declining demand

Factors Affecting Tacit Collusion:

Collusion has been frequently observed in the industries listed below. Identify which

of above factors make collusion particularly likely in these industries.

• School milk

• Lysene and other animal food additives:

School Milk

Demand is inelastic because consumers don’t pay the price

Transportation costs limit market scope therefore creating entry barriers

Lysense :

Extreme economies of scale

Few sellers

Very homogenous costs and Inelastic demand since the additives are a very small cost of the good

Antitrust Policy Toward Explicit Collusion:

What is the legal policy toward explicit price-fixing arrangements in the United States?

Identify two court cases that provide precedent for your conclusion.

Policy: Explicit collusion is per se illegal under Sherman Act - meaning it’s automatically unlawful, no need to prove harm to consumers or market

Cases:

1) Addyston Pipe (1899)

2)Trenton Potteries (1927)

Conscious Parallelism:

Describe how the legal standard for illegal parallel behavior evolved across three key cases: American Tobacco (1946), Theatre Enterprises (1954), and Ethyl (1984). For each, explain what kind of coordinated behavior was considered illegal at the time.

American Tobacco (1946): conscious parallelism is illegal

Theatre Enterprises (1954): reversal of previous standard - parallel prices do not necessarily imply collusion

Ethyl (1984): Alleged conspiratorial behavior requires that the gov show no legitimate business purpose of the price change

Deviations from Standard Assumptions that may generate higher prices in Bertrand Competition

Bounded Rationality

Product Differentiation

Capacity Restraints