ACT Math - Formulas

Vertical Angles

Formed by 2 intersecting lines or segments. Always congruent.

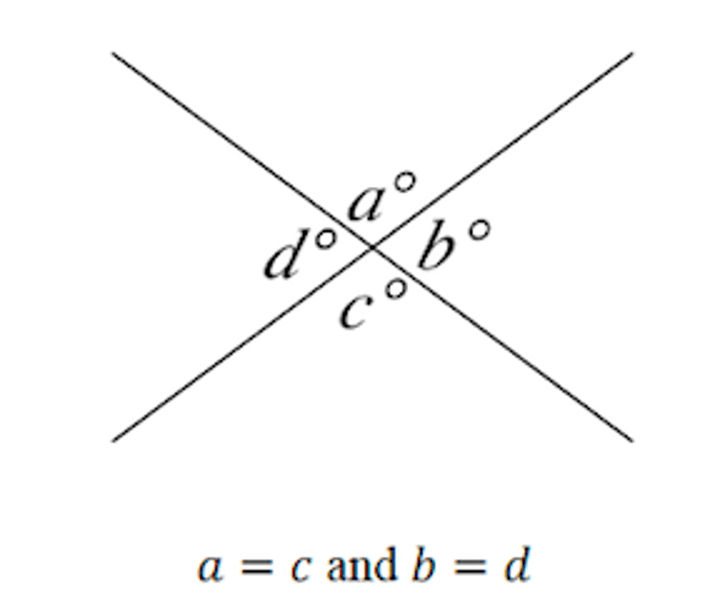
Supplementary Angles

Two angles that form a line and add up to 180°.

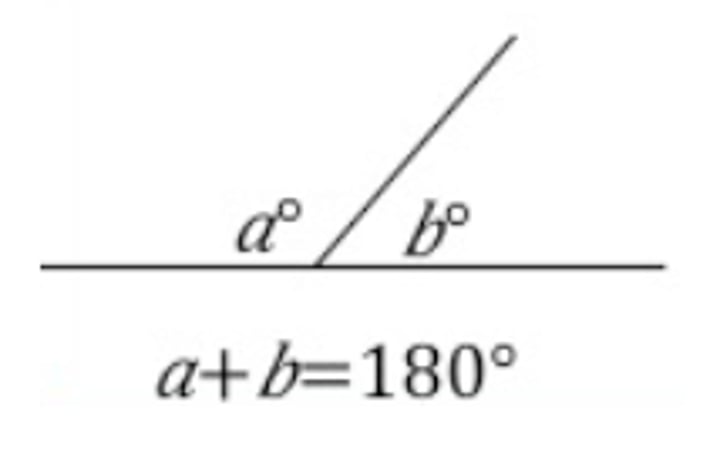
Right Angle

An angle that measures 90°.

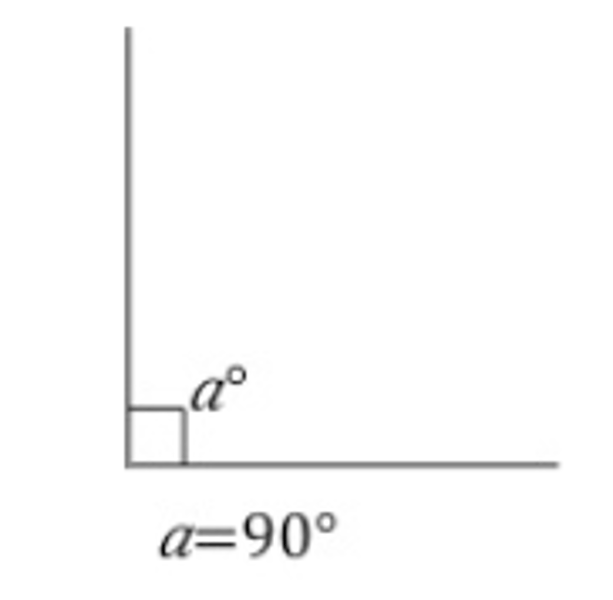
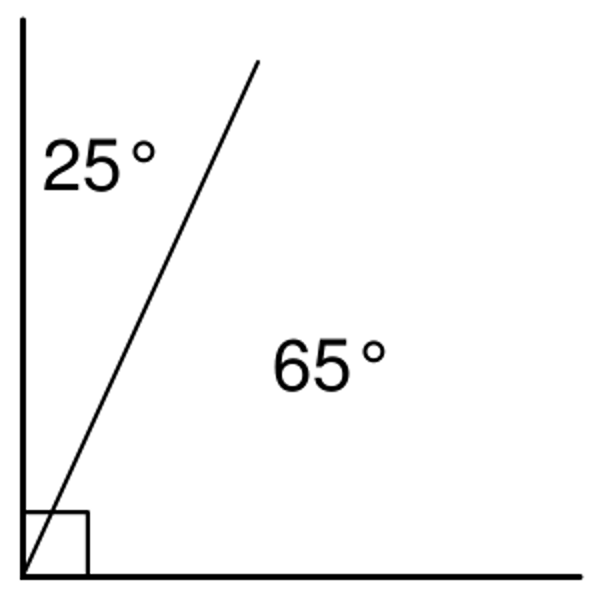
Complimentary Angles

Two angles that add up to 90°.

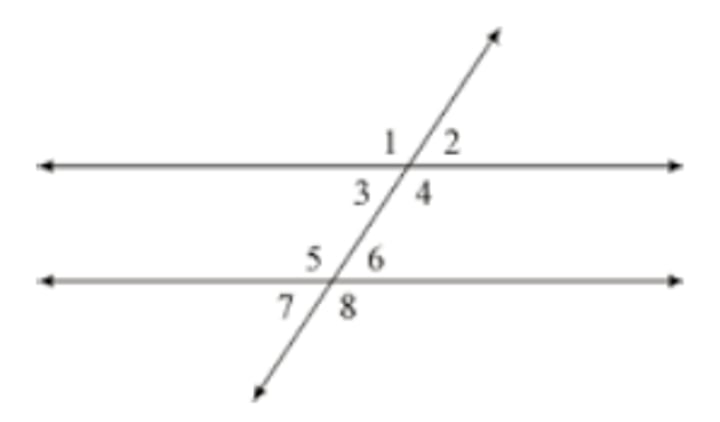
Alternate Interior Angles (Parallel Lines)

Ex. 3 & 6 are congruent

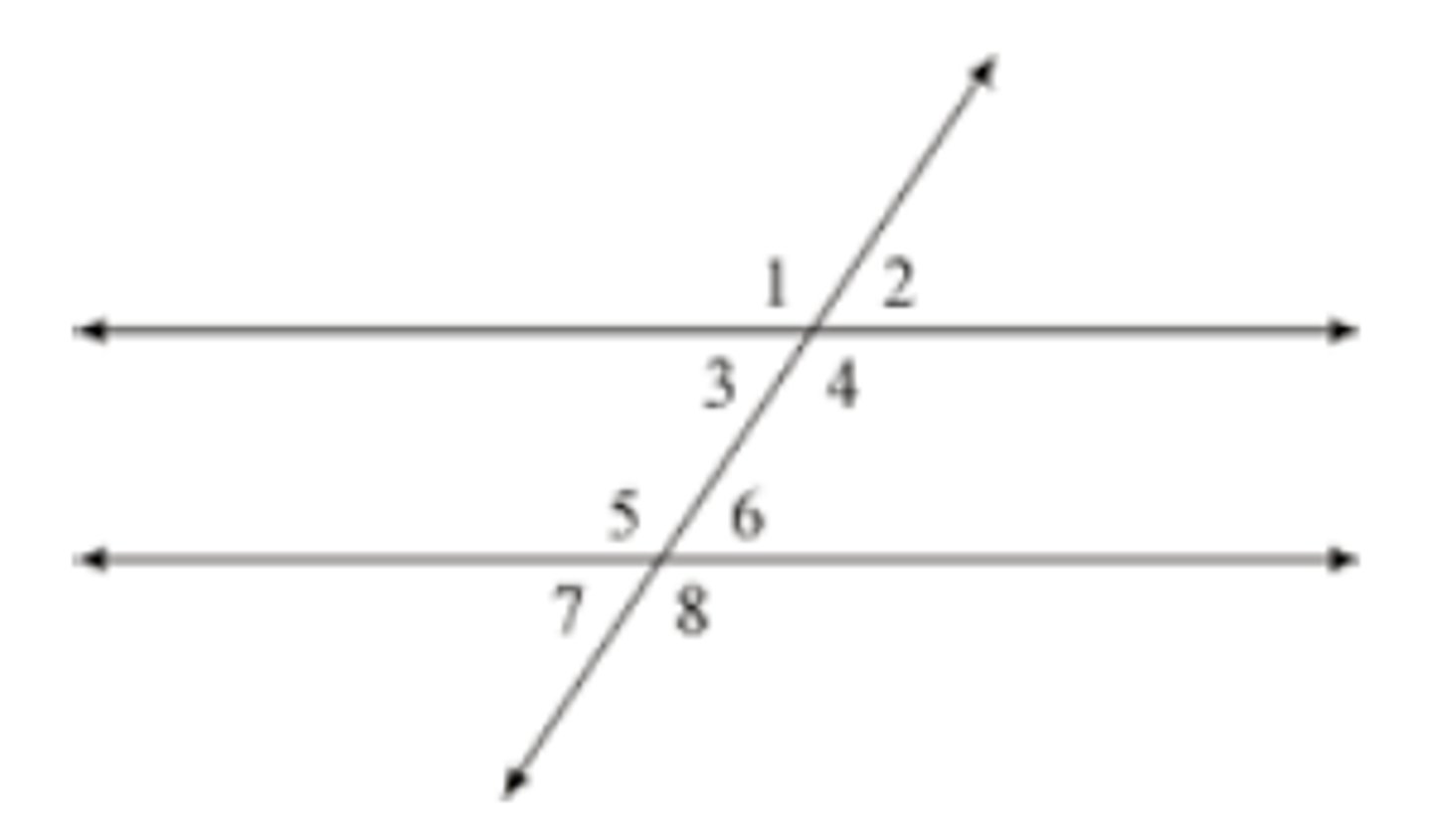
Alternate Exterior Angles (Parallel Lines)

Ex. 1 & 8 are congruent

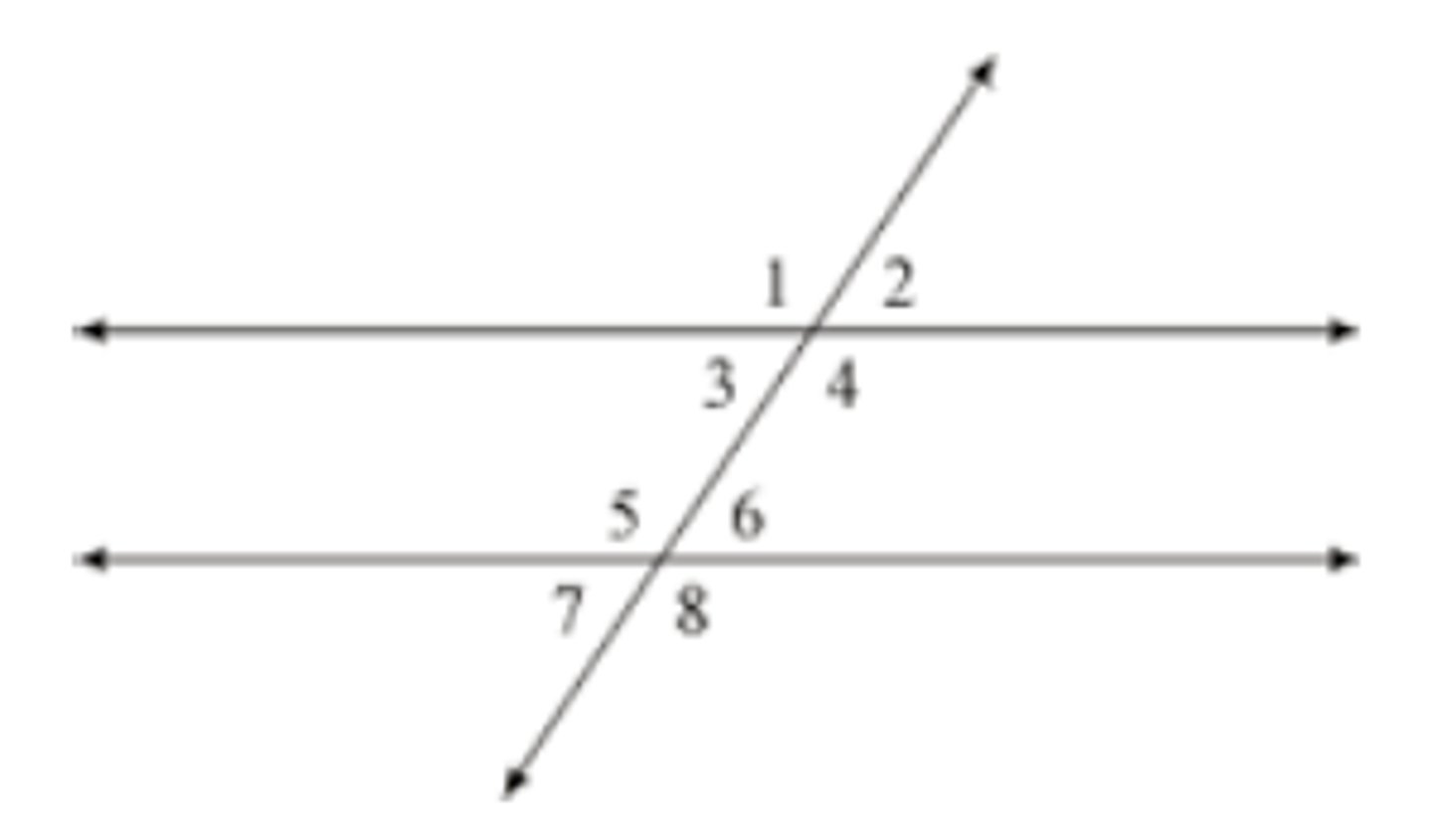
Corresponding Angles (Parallel Lines)

Ex. 1 & 5 are congruent

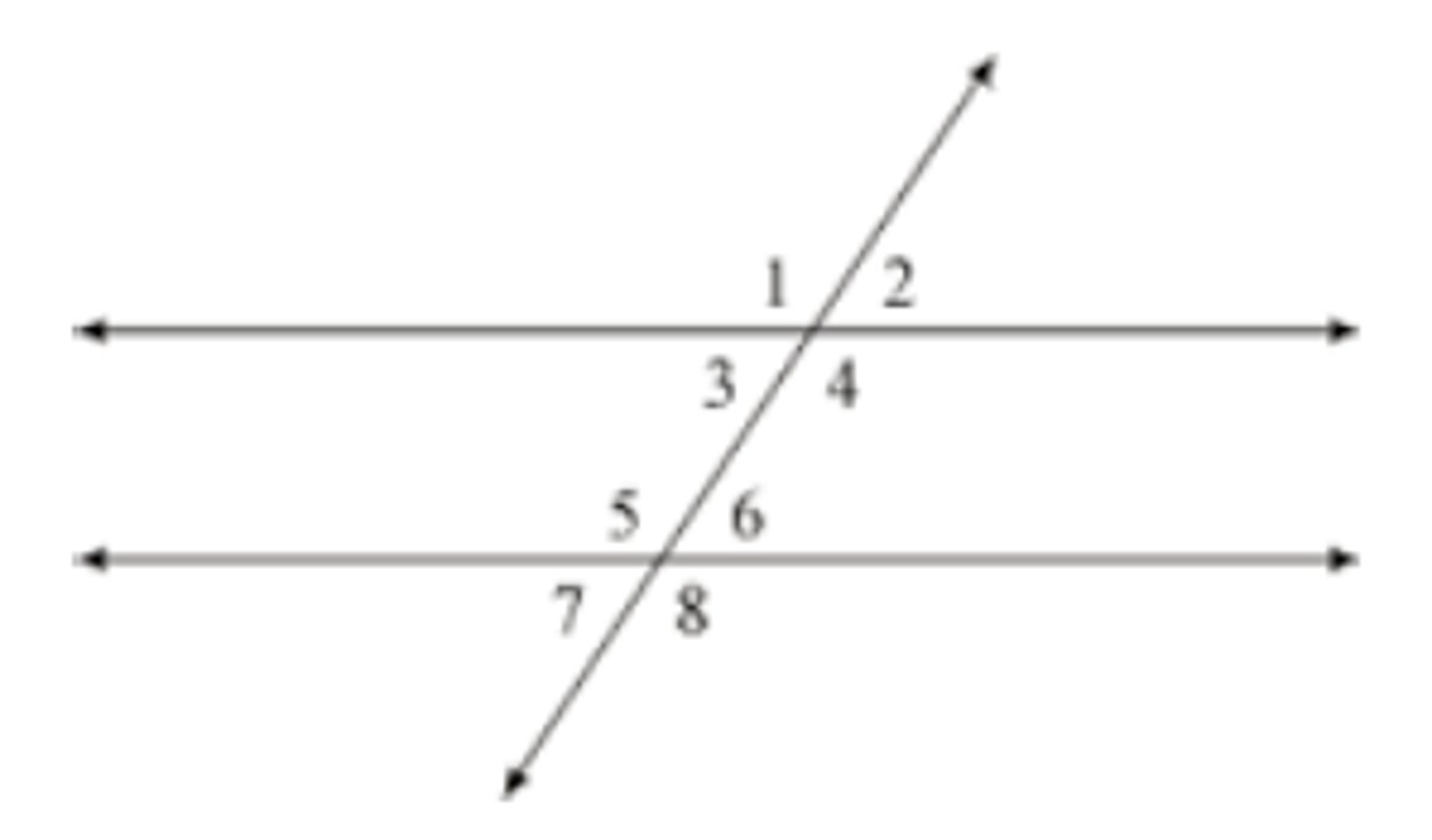
Same Side Interior Angles (Parallel Lines)

Ex. 3 & 5 add up to 180º

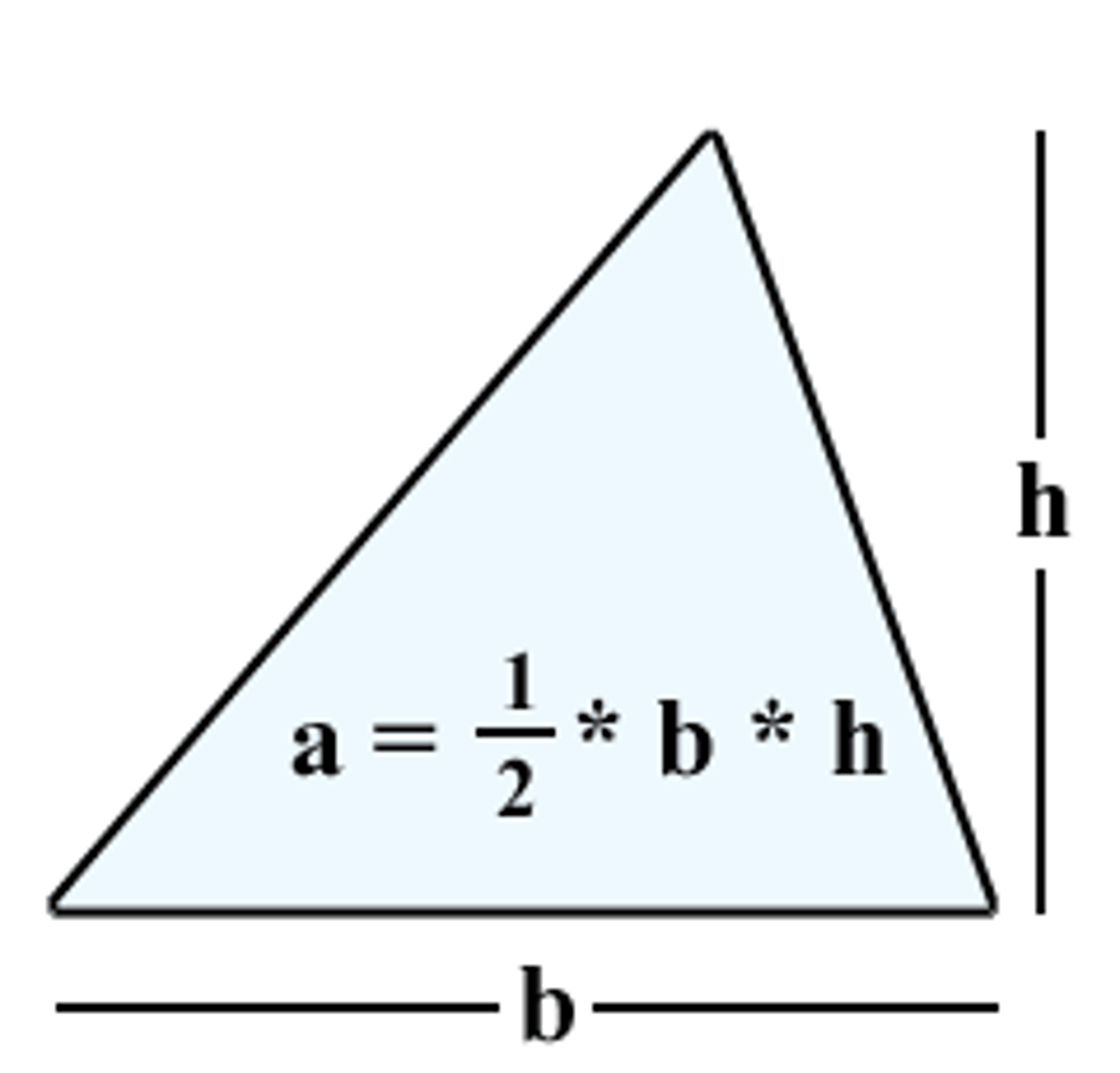
Area of a Triangle

A=½(Base)(Height)

A=½bh

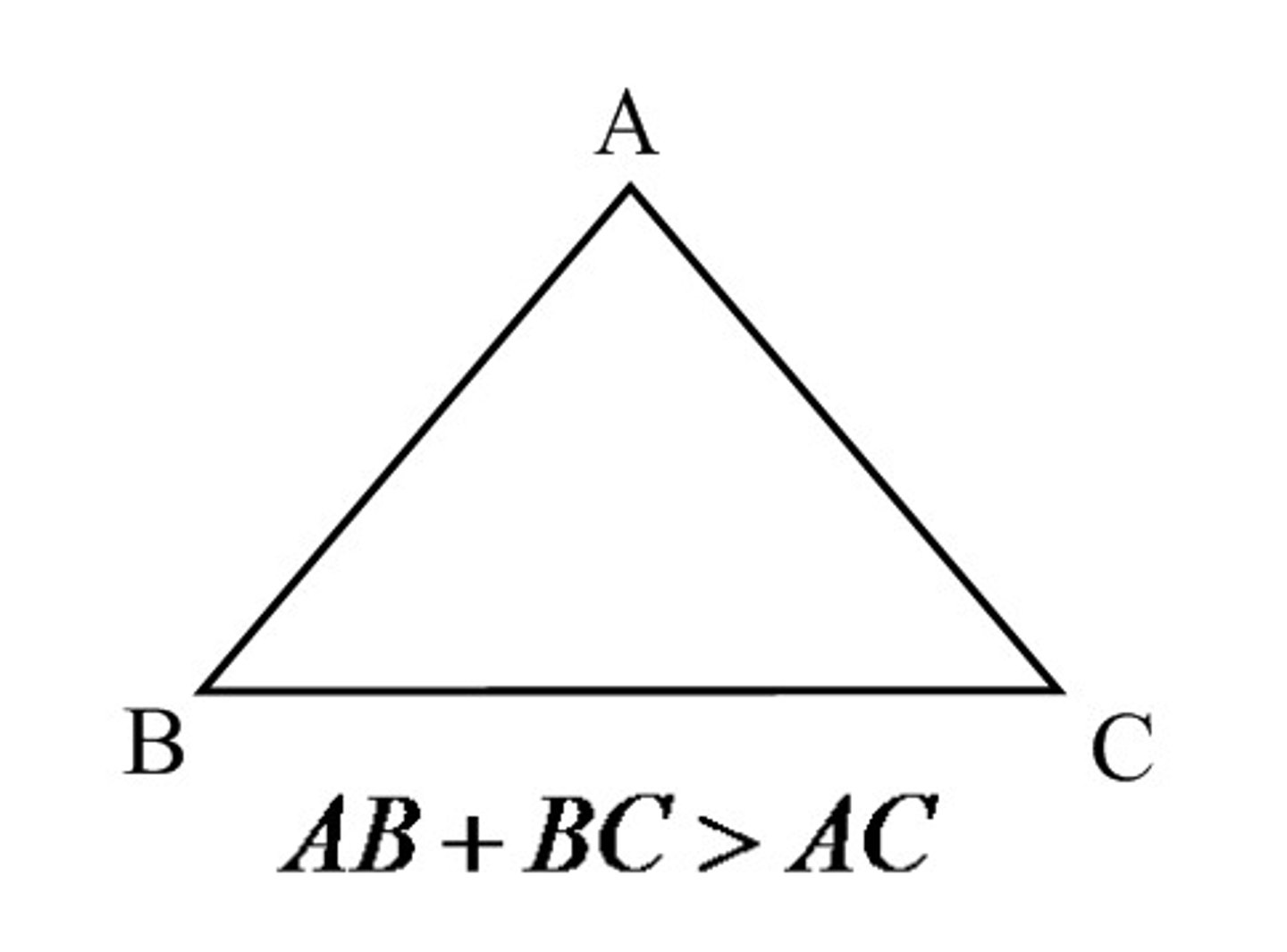
Triangle Inequality Theorem

The sum of the 2 shortest sides of a triangle is always greater than the length of the third side.

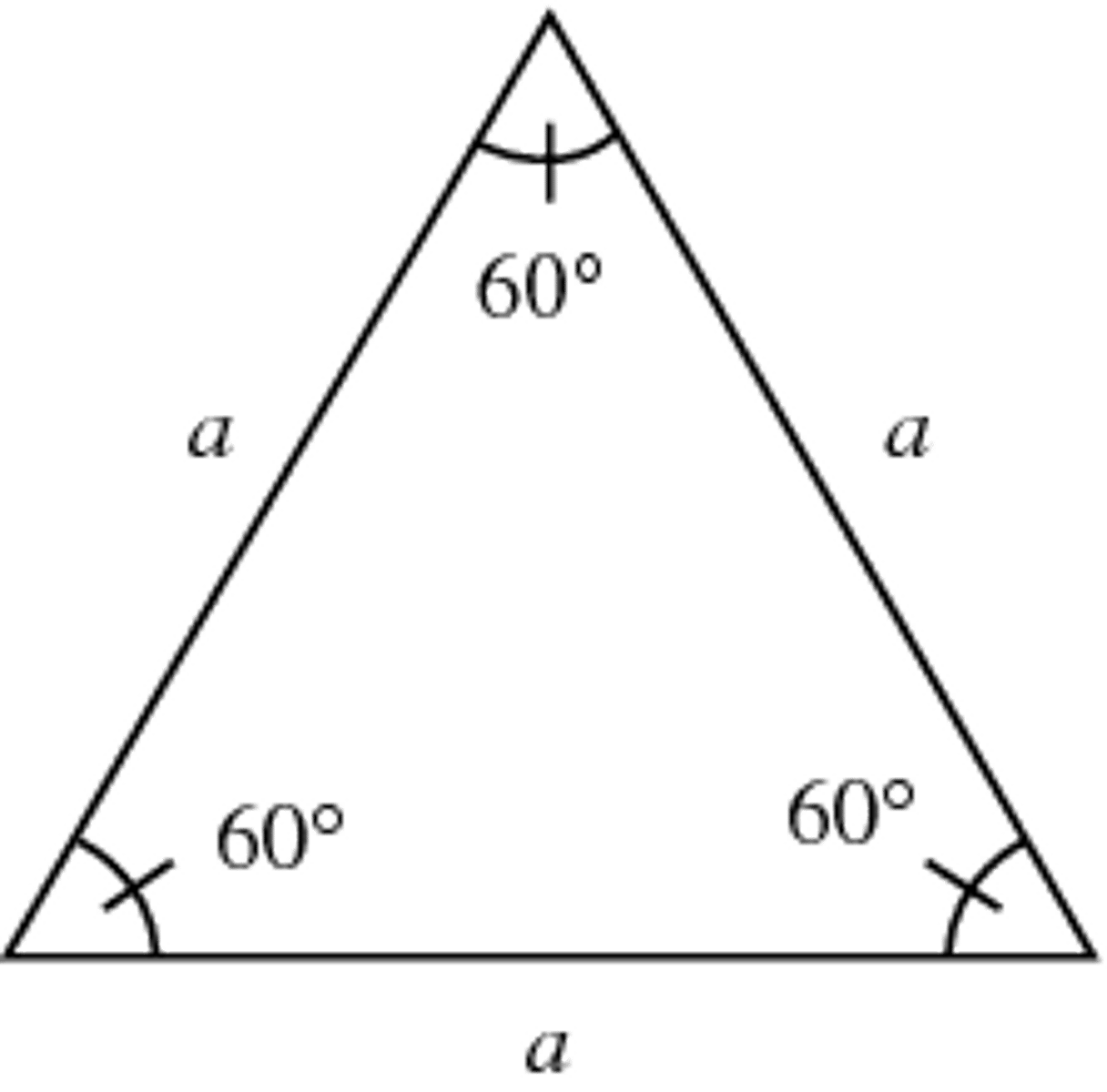
Equilateral Triangle

A triangle in which all three sides are equal and all three interior angles are 60°.

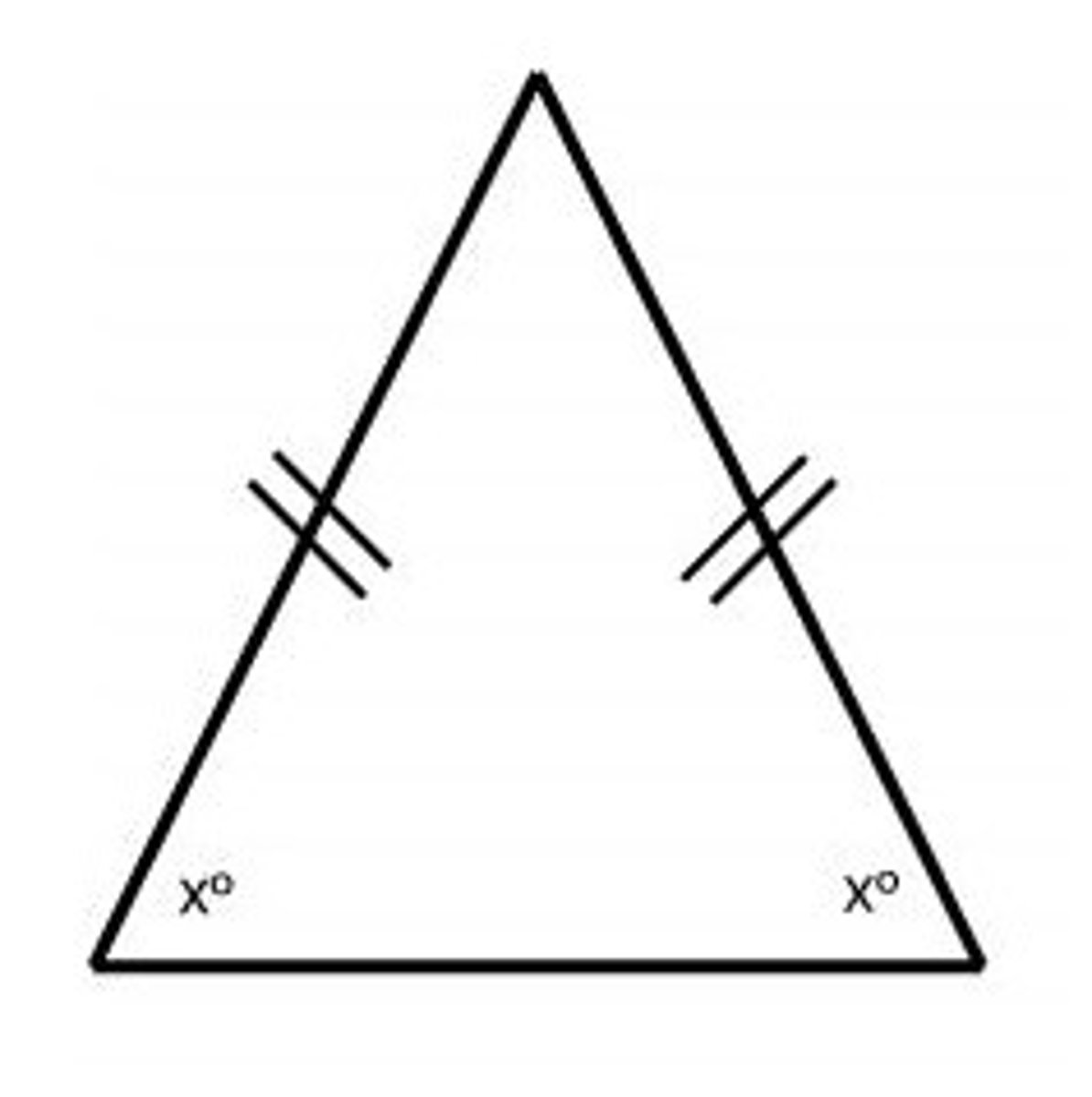
Isosceles Triangle

A triangle with two equal sides. Base angles (angles across from the congruent sides) are also equal.

Proportionality in Triangles

In every triangle, the longest side is opposite the largest angle and the smallest side is opposite the smallest angle.

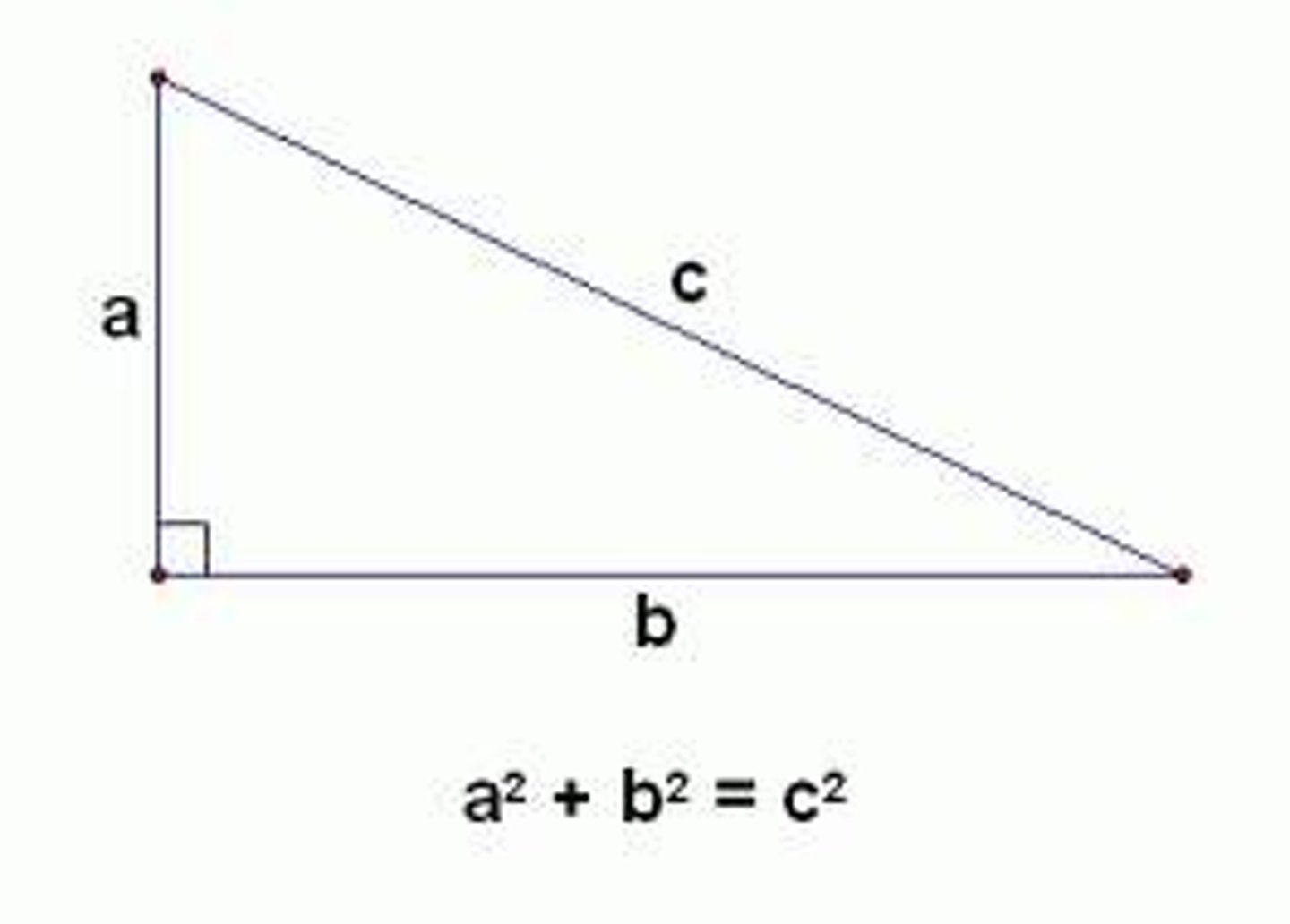
Pythagorean Theorem

Used to find the missing side of a right triangle.

"c" is always the length of the hypotenuse.

a²+b²=c²

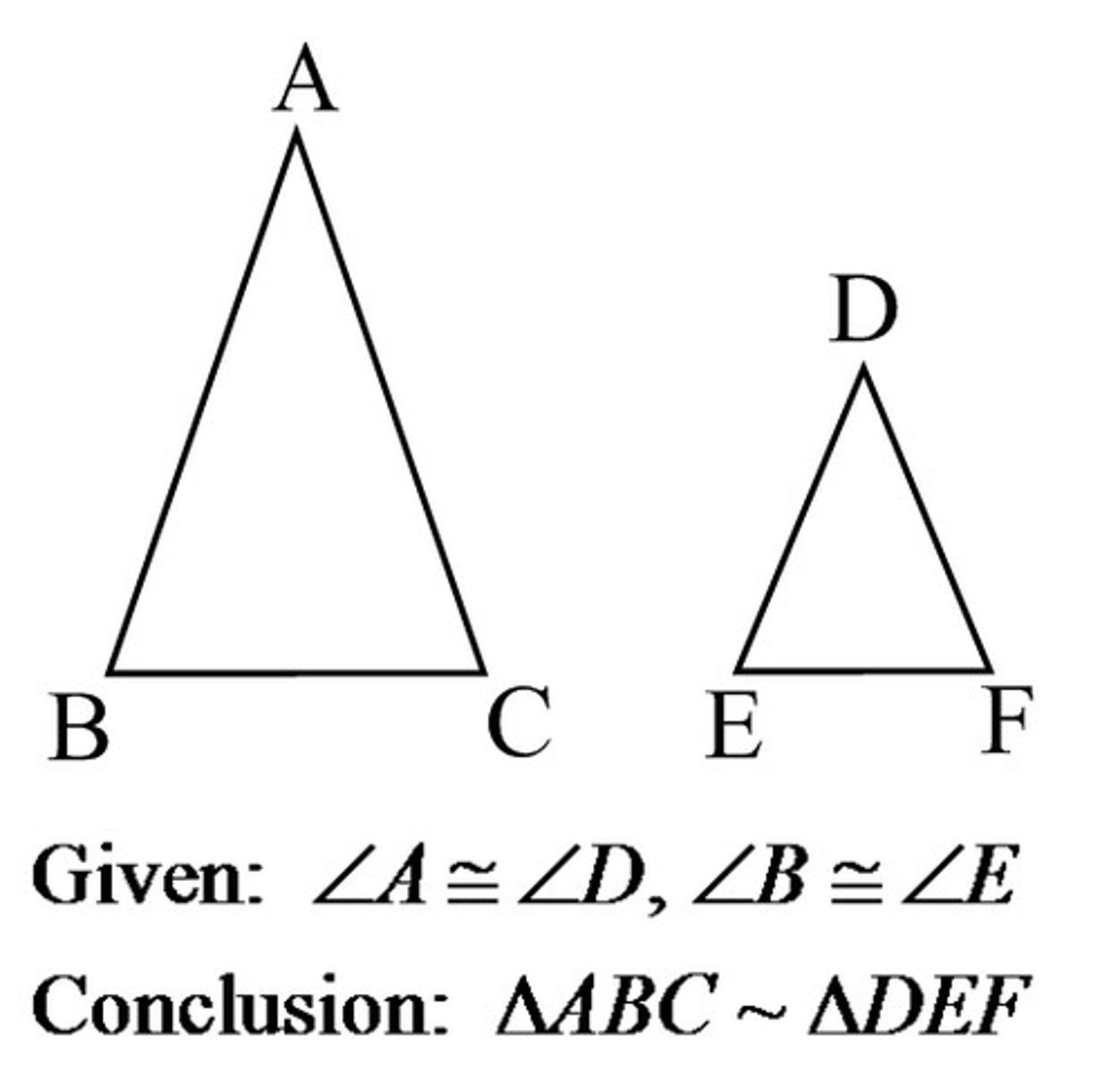
Similar Triangles

Triangles that have the same angle measures but different side lengths. Solve by setting up a proportion.

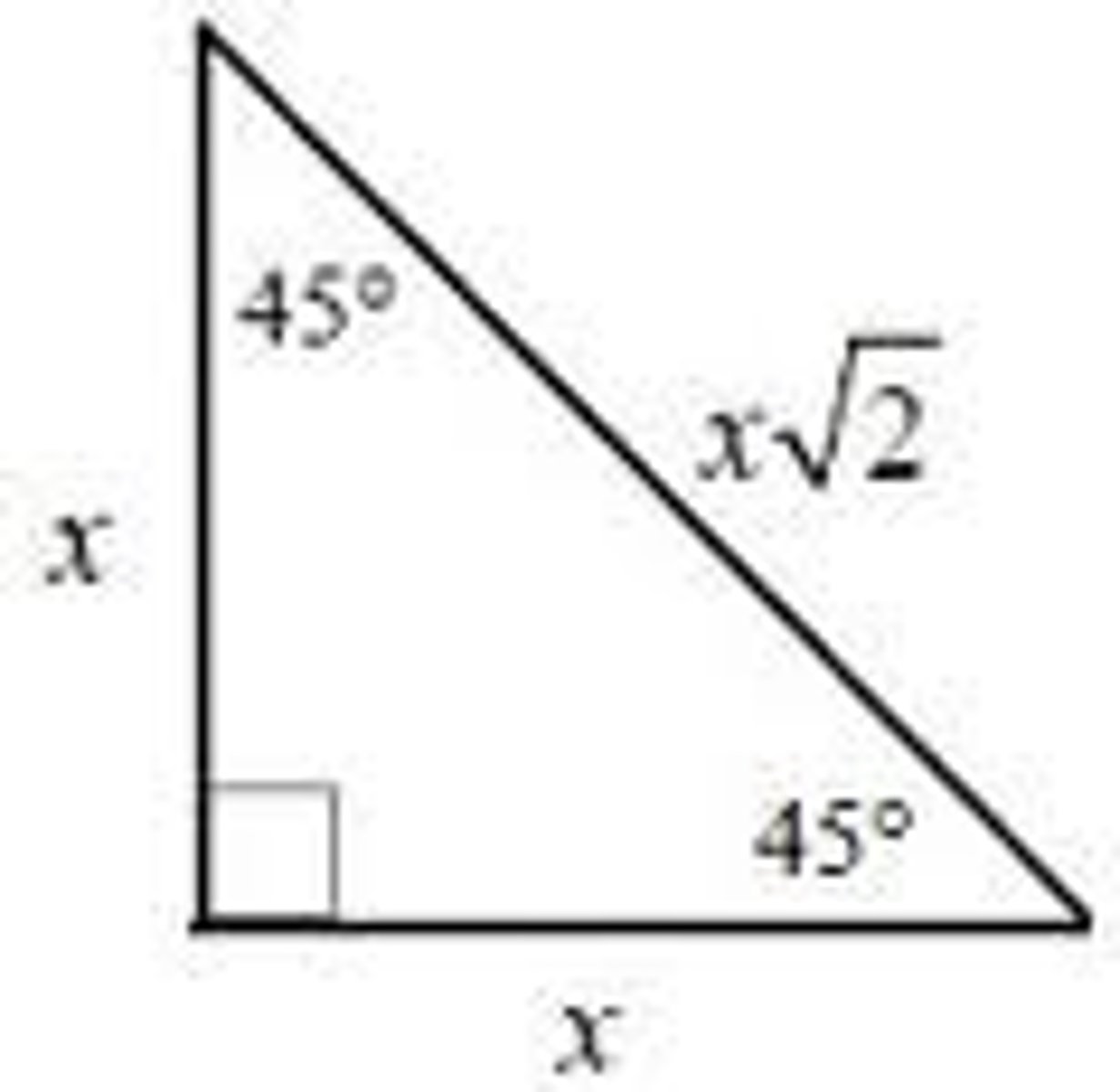
45-45-90 Special Triangle

Always in the ratio 1:1:√2

Isosceles right triangle

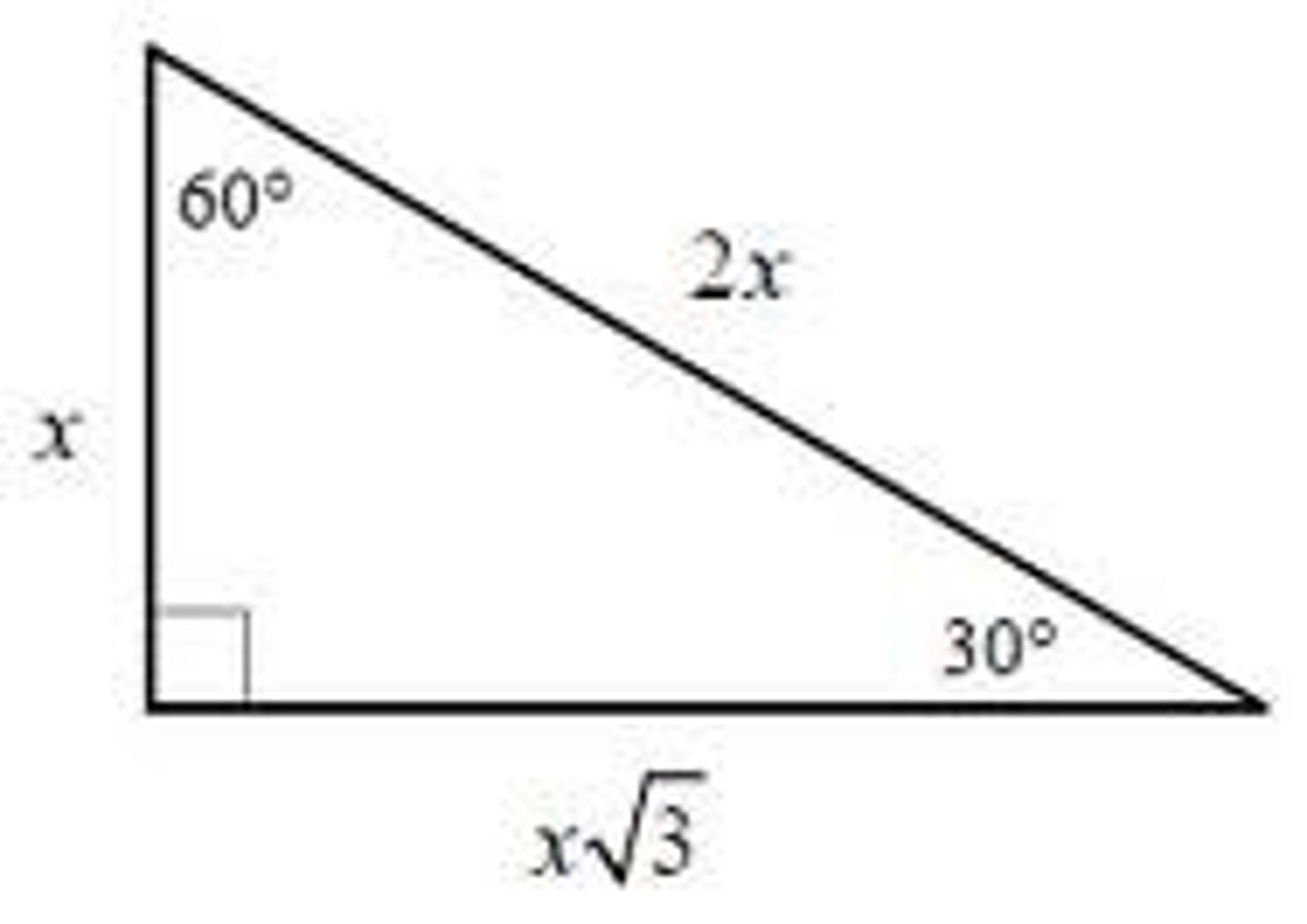
30-60-90 Special Triangle

Always in the ratio 1:√3:2

Pythagorean Triple

Three integers that, as side lengths of a triangle, form a right triangle.

Ex. 3/4/5 or 5/12/13

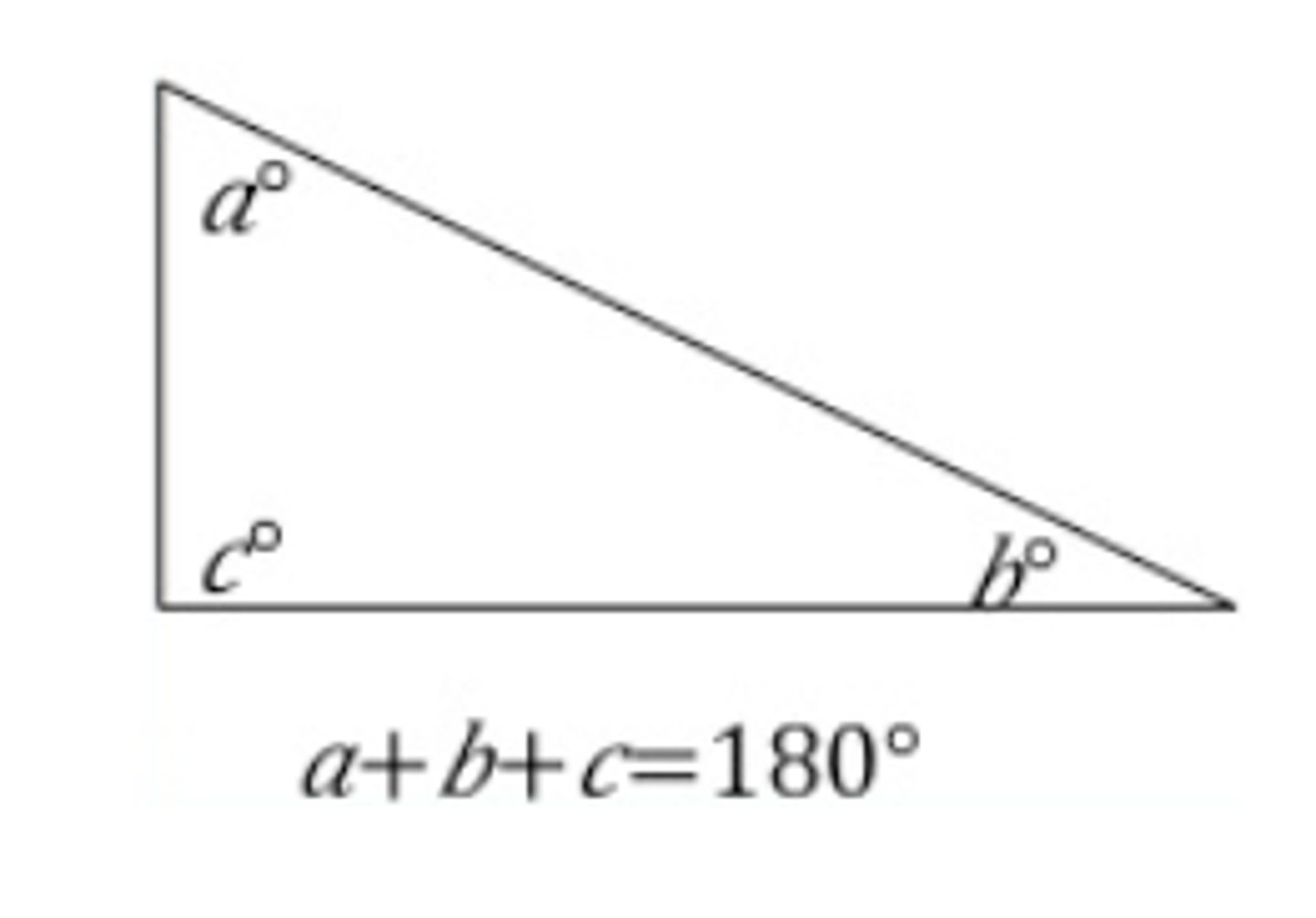
Degree Measure of a Triangle

The inside angles of a triangle always add up to 180°.

Area of a Circle

A=πr²

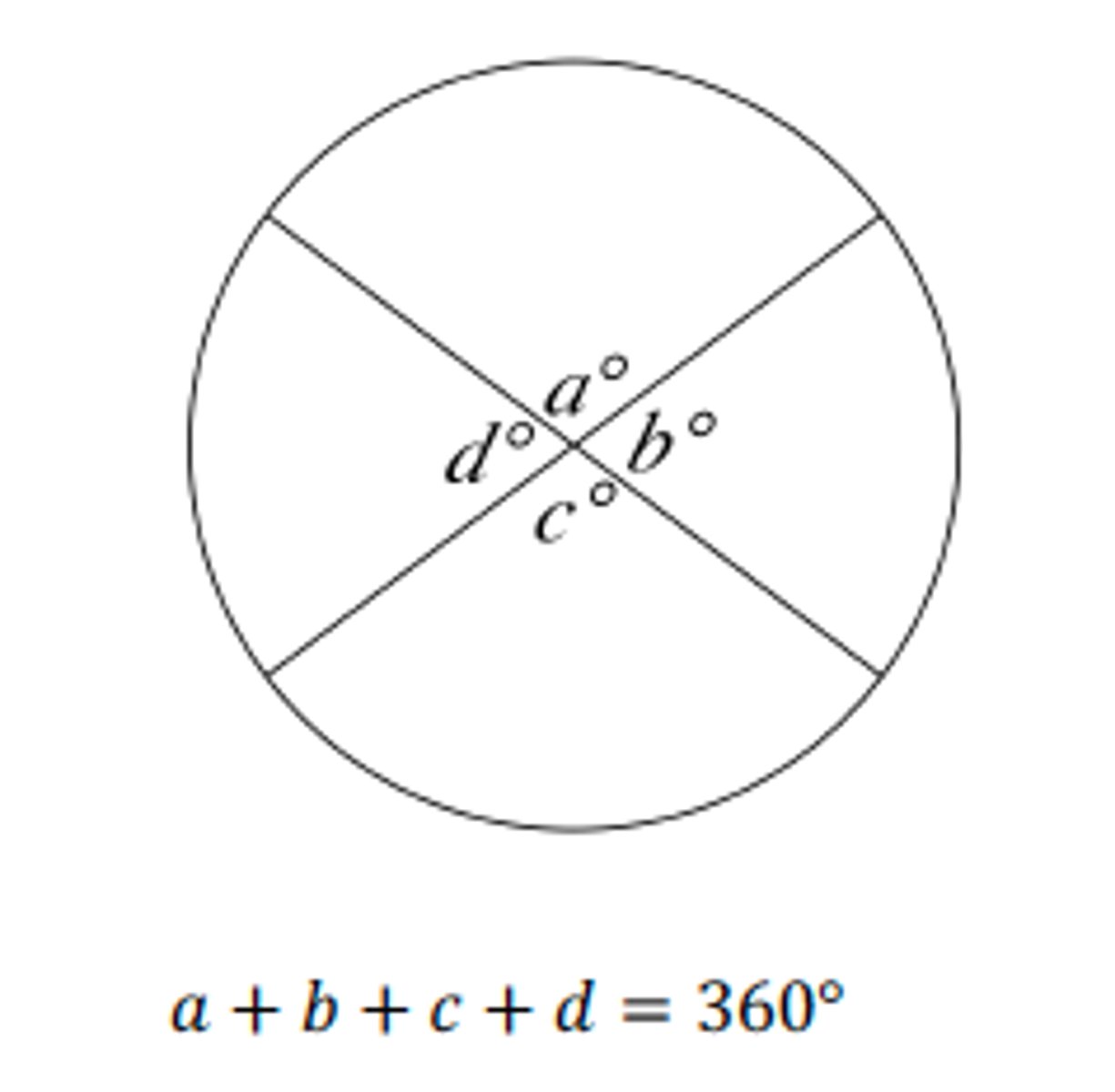
Degree Measure of a Circle

The central angles of a circle add up to 360°.

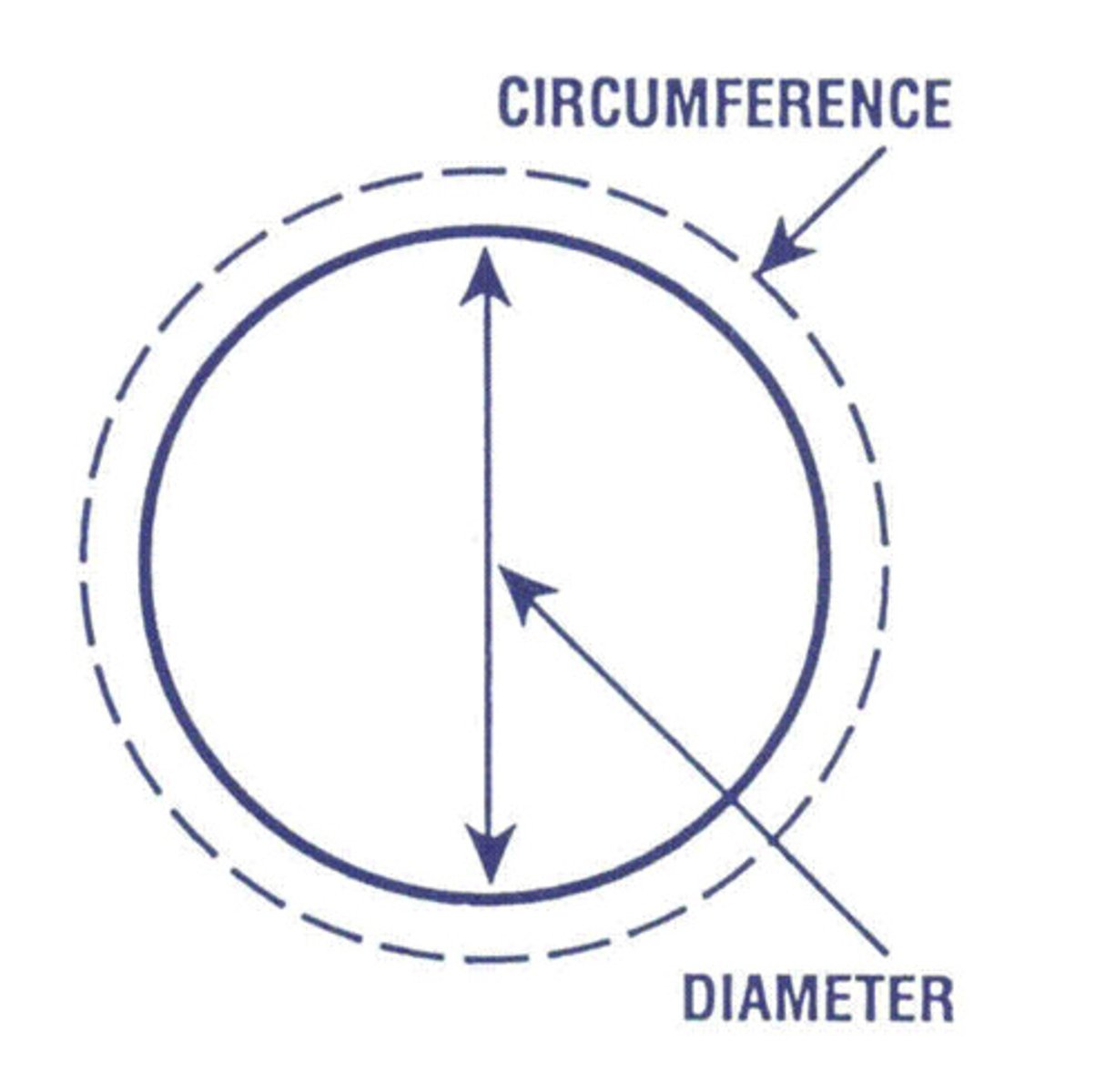
Circumference of a Circle

C=2πr or C=πd

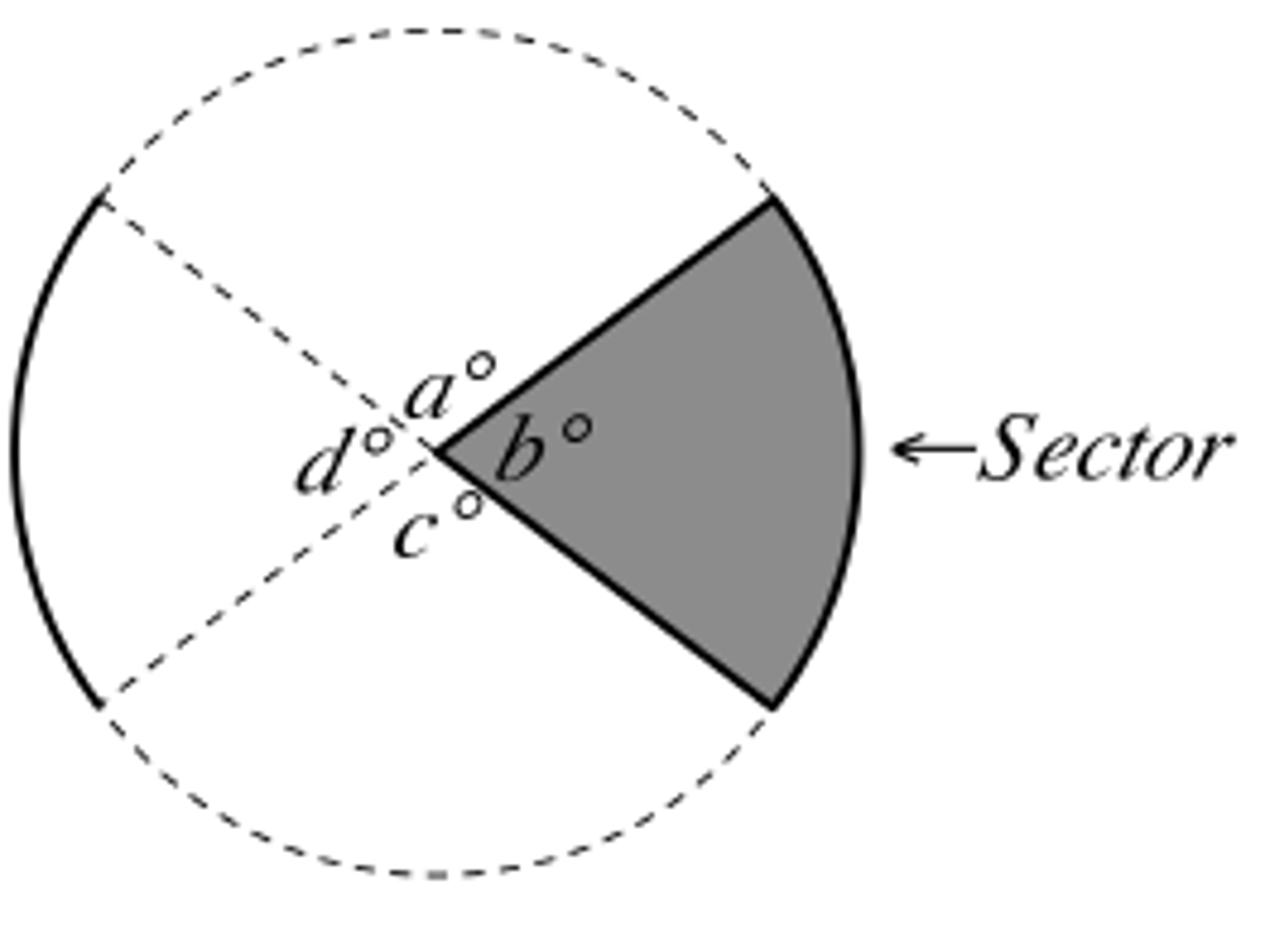
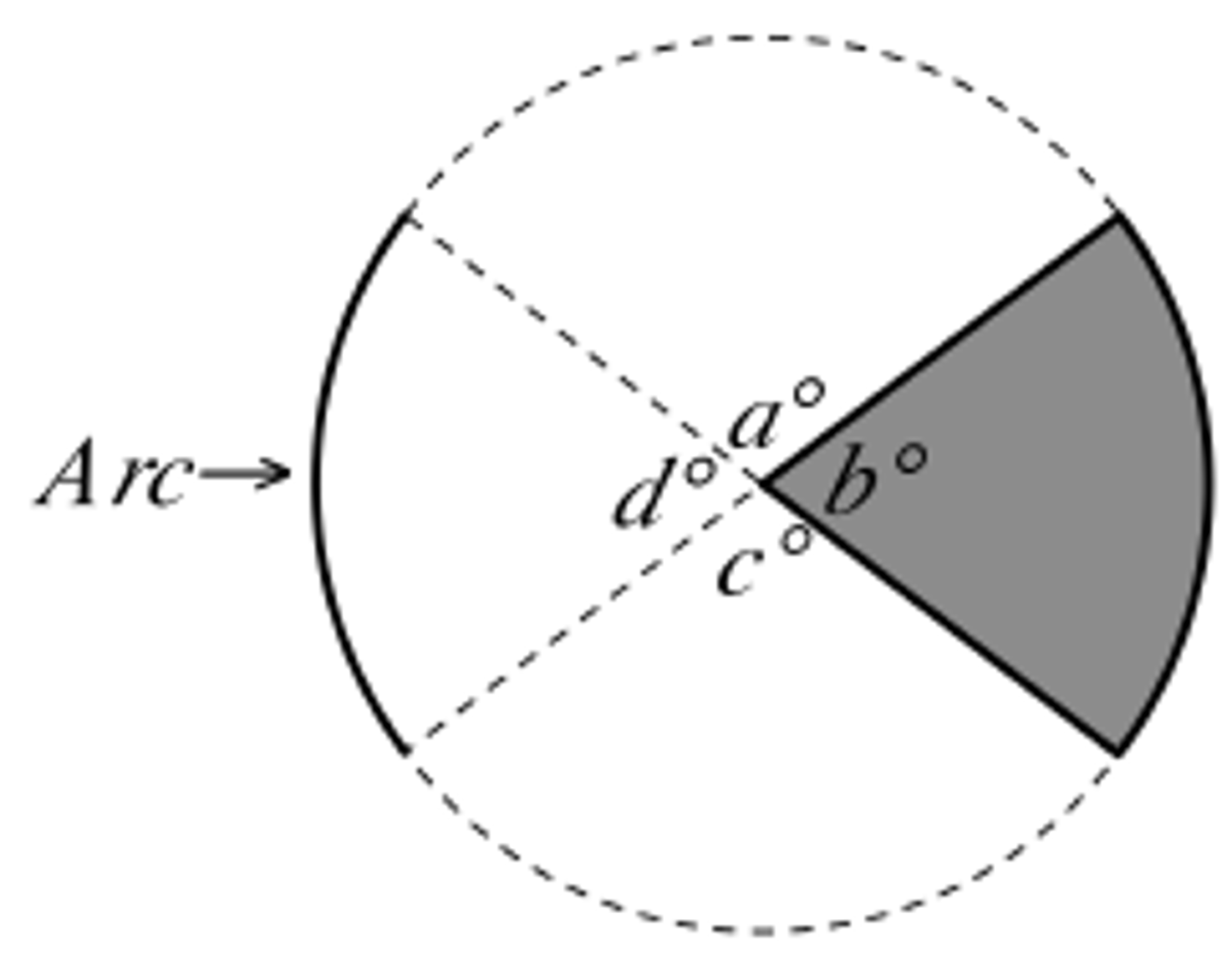
Area of a Sector (Circle)

(n/360)(πr²), where n is the central angle.

Arc Length of a Sector (Circle)

(n/360)(2πr), where n is the central angle.

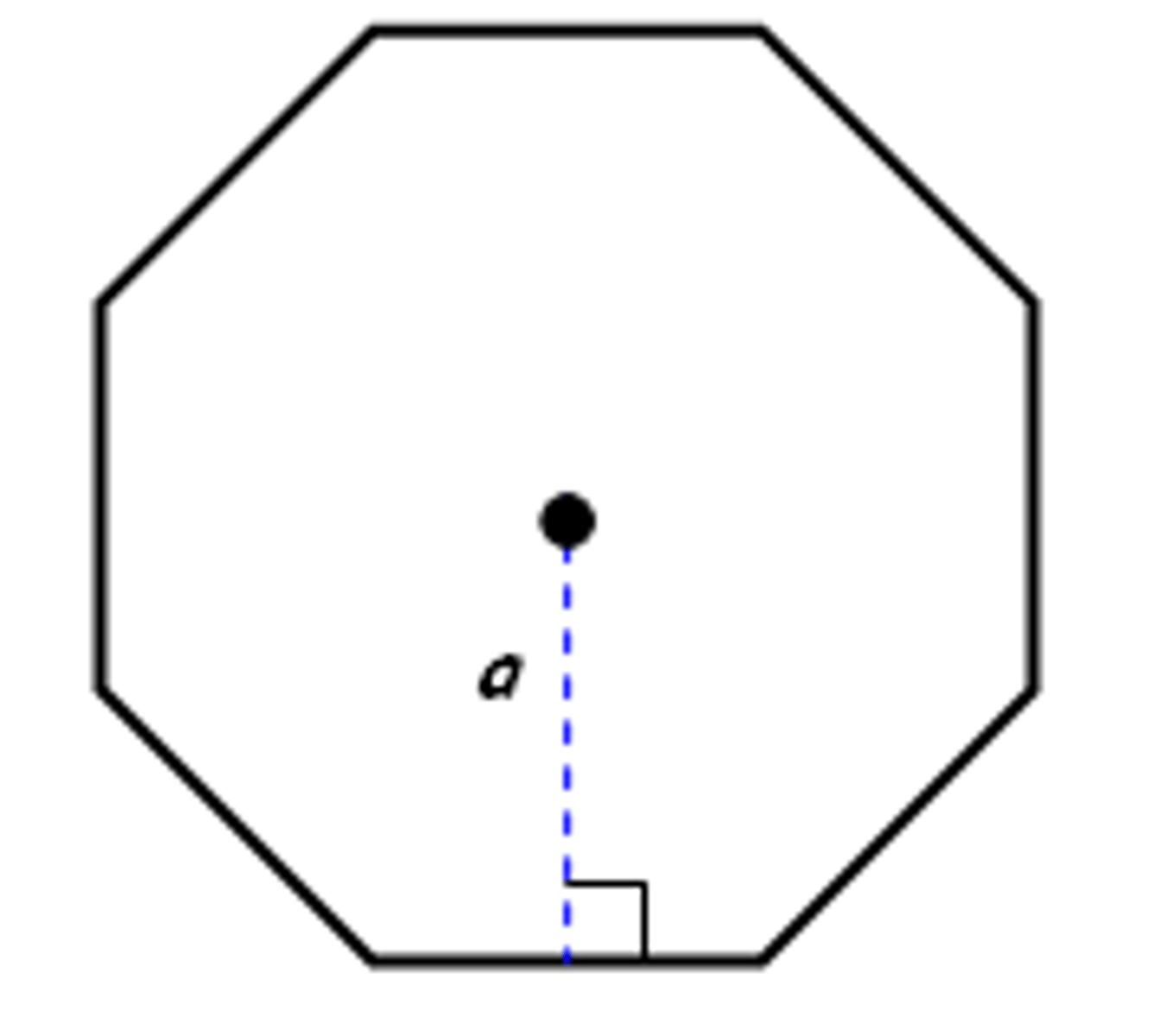
Area of a Polygon

A=½aP, where a is the apothem and P is the perimeter.

Sum of Interior Angles of a Polygon

Sum=180(n-2), where n is the number of sides.

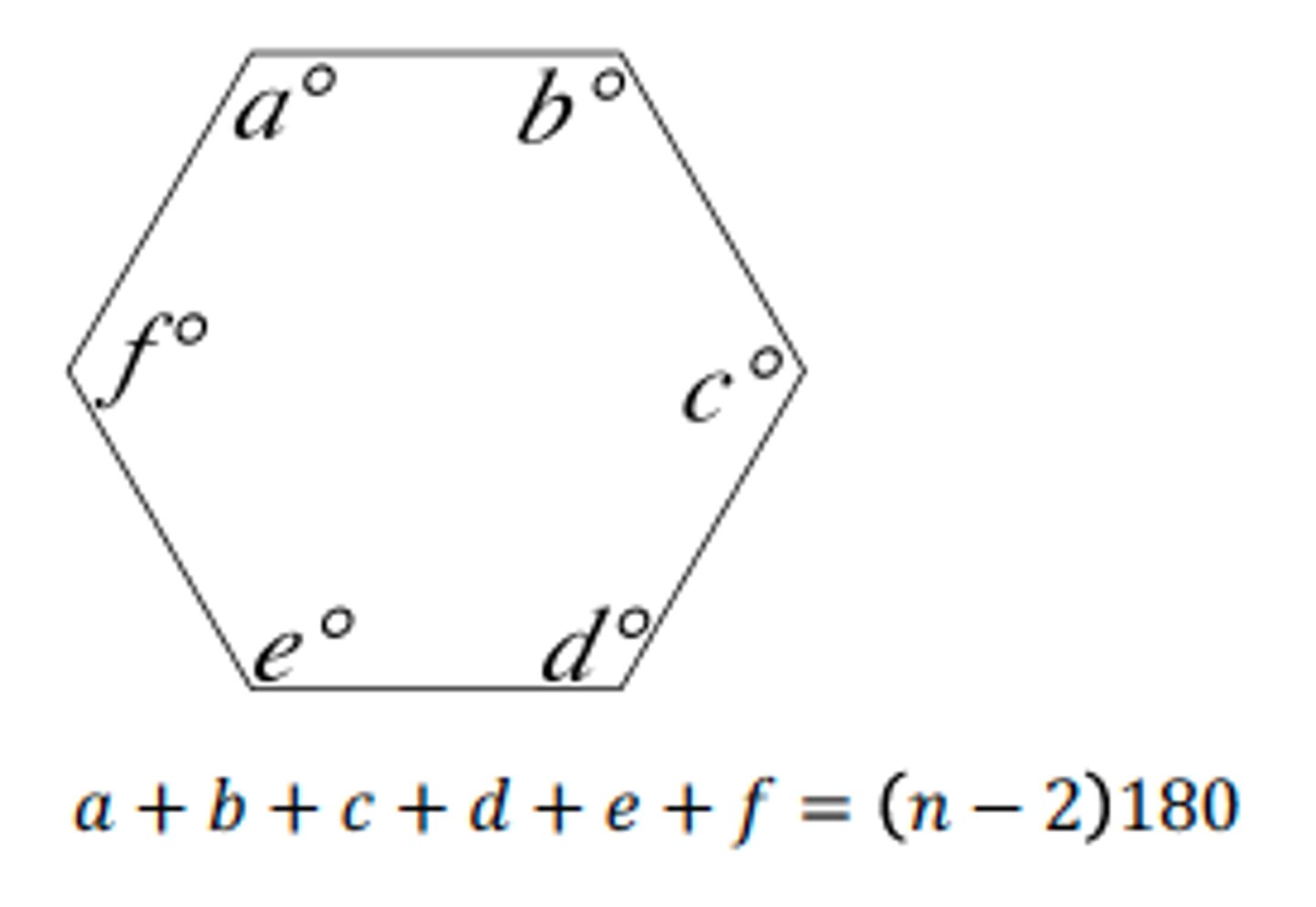
Interior Angle of a Polygon

Where n is the number of sides

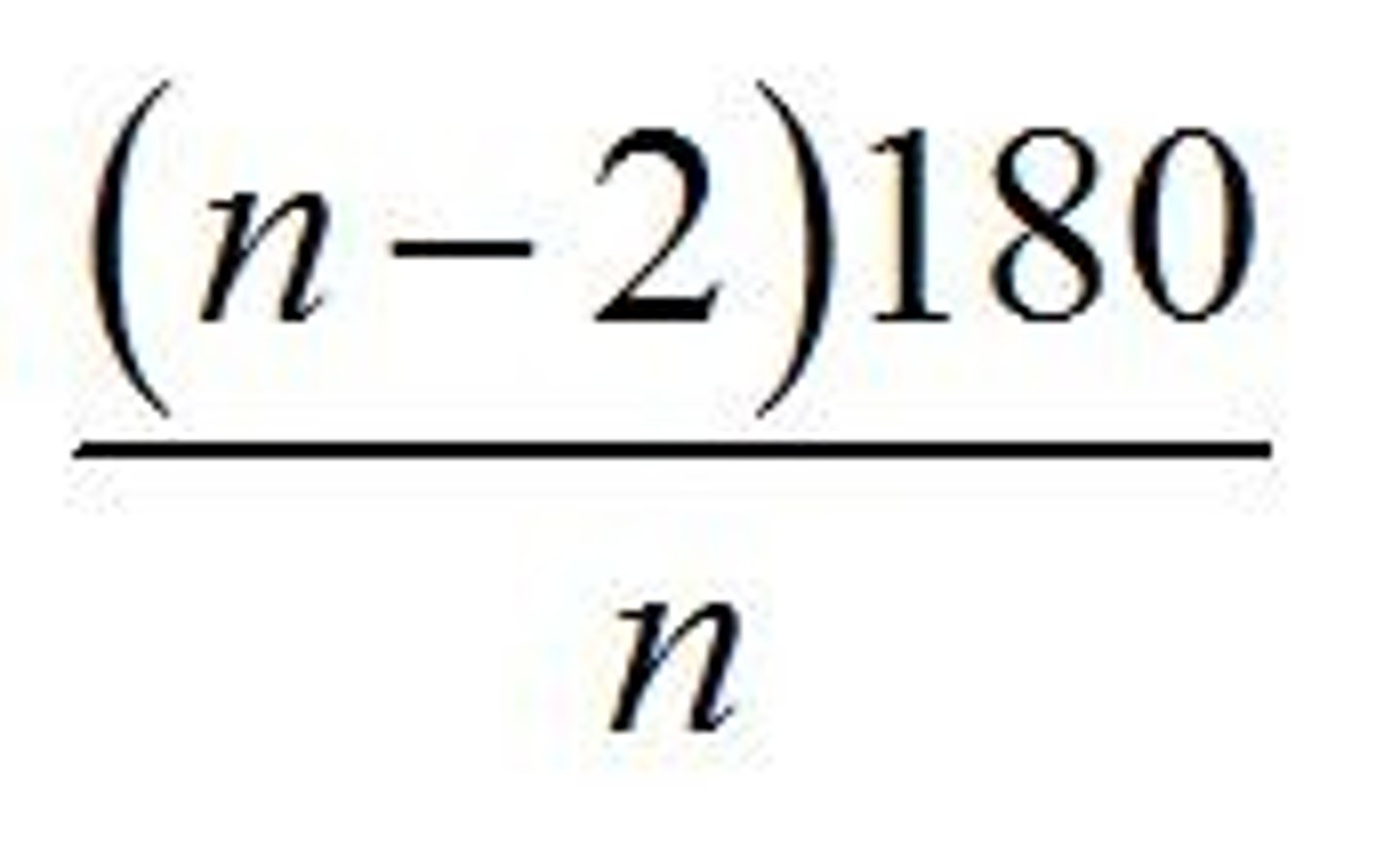
Degree Measure of a Quadrilateral

The interior angles of a quadrilateral add up to 360º.

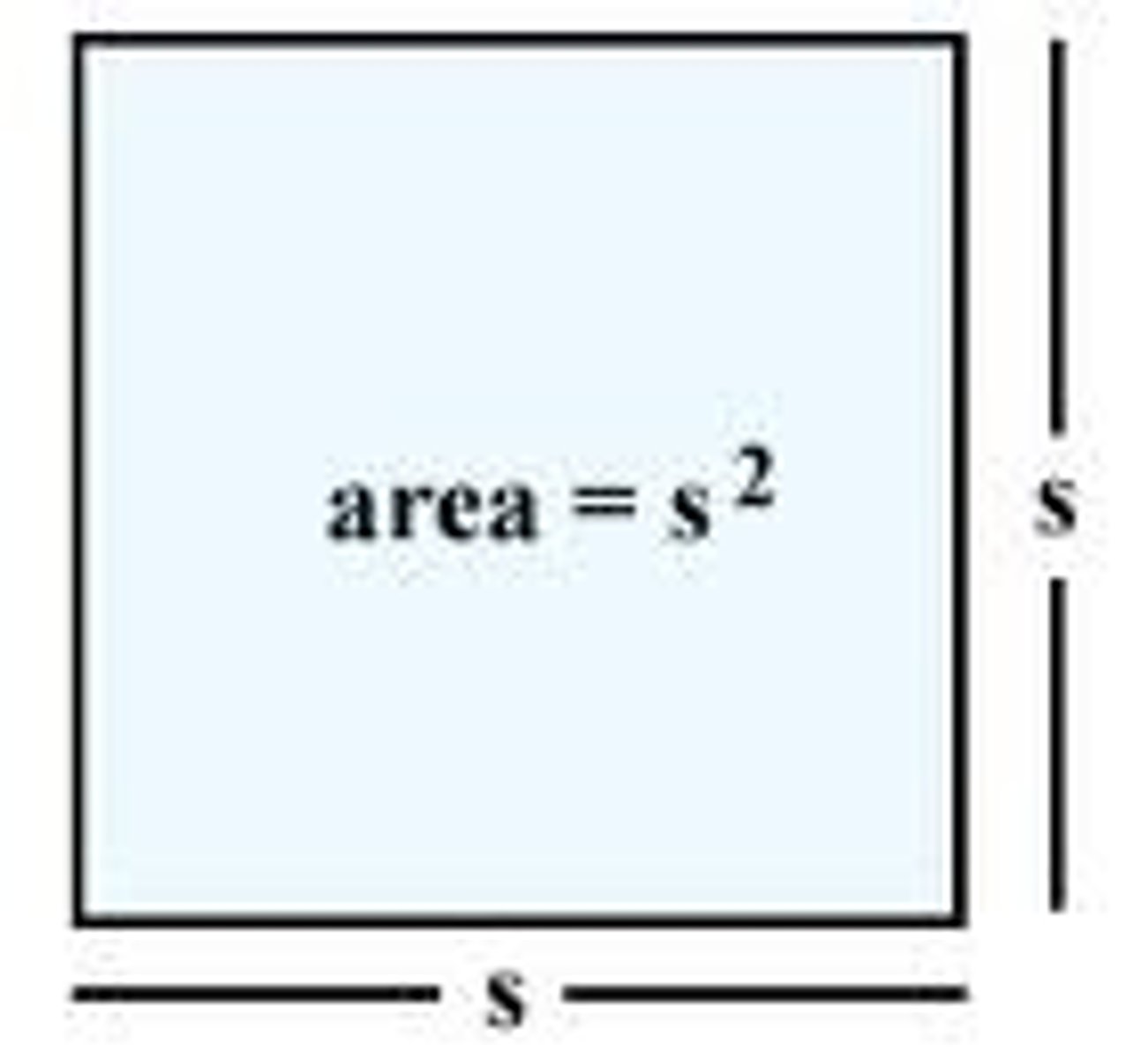
Area of a Square

A=(side)(side)

A=s²

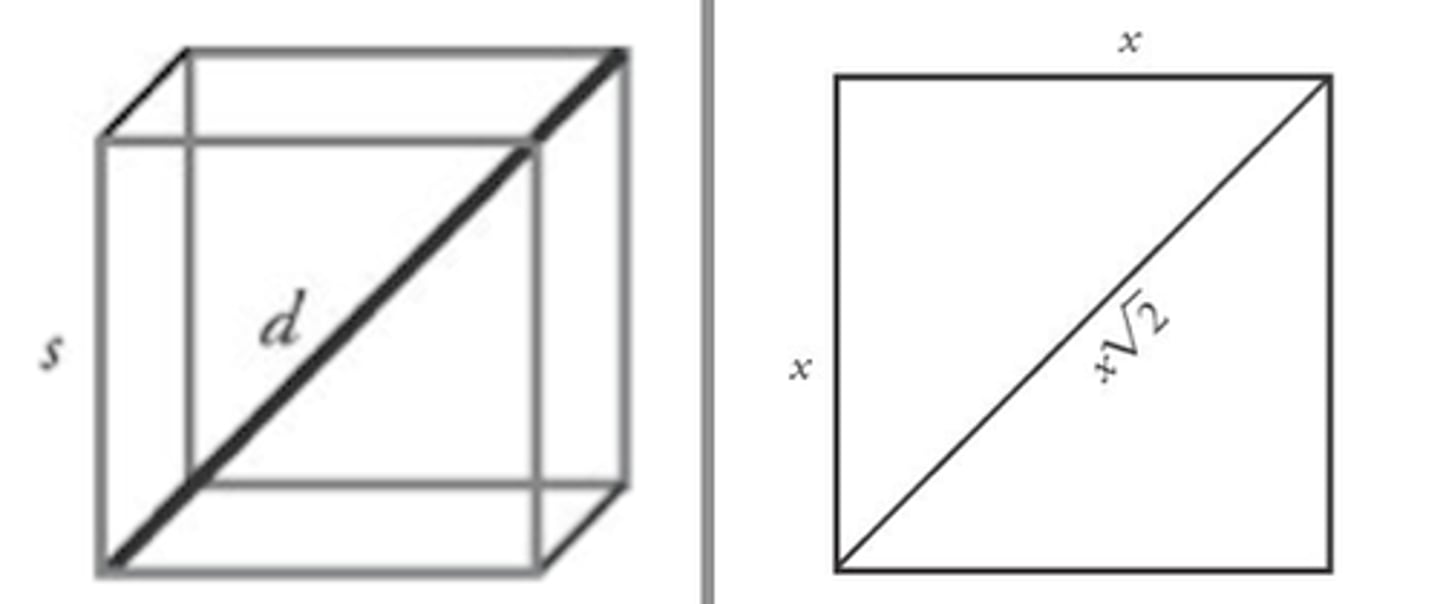
Diagonal of a Square

Diagonal=side(√2)

D=s√2

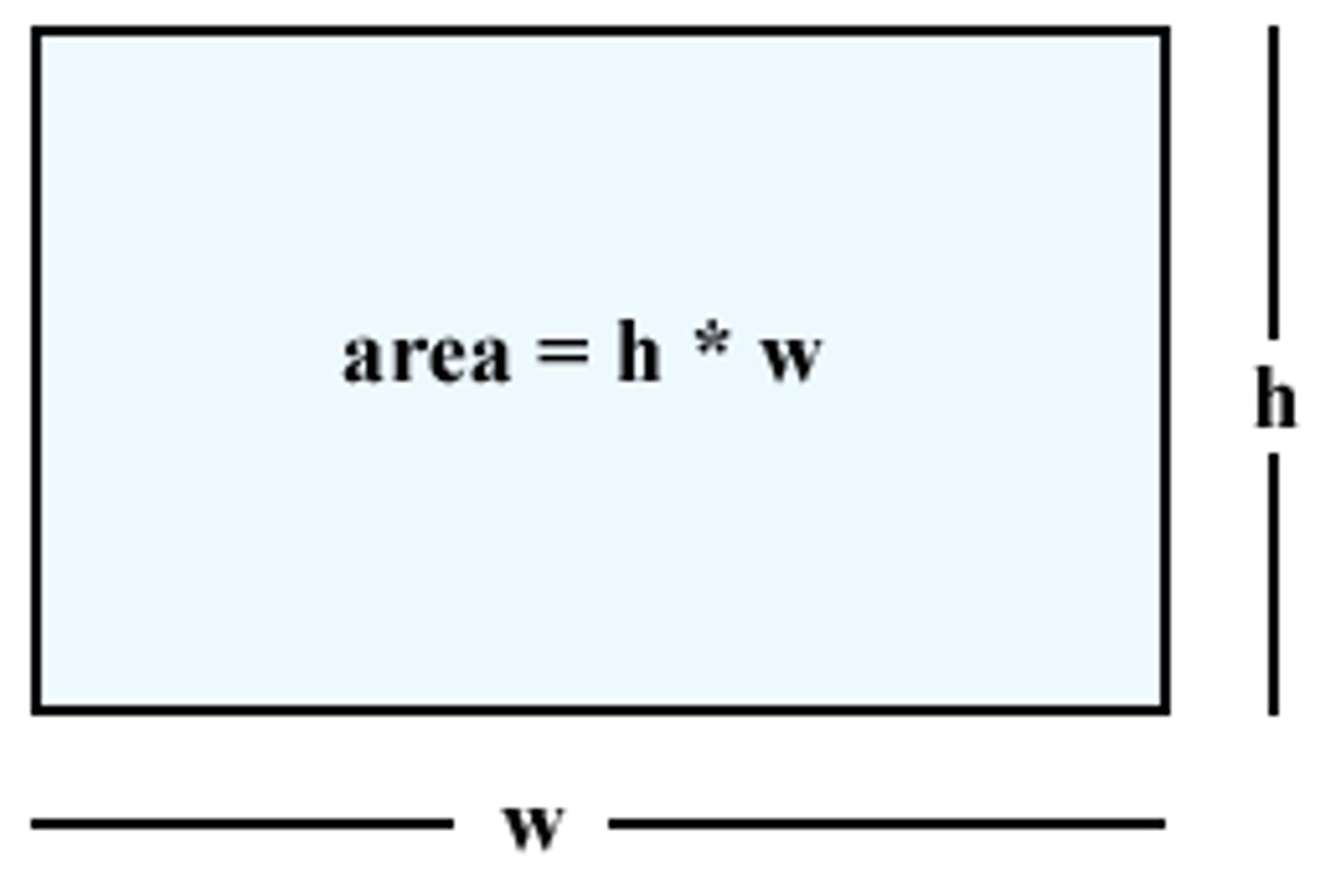
Area of a Rectangle

A=(length)(width)

A=lw

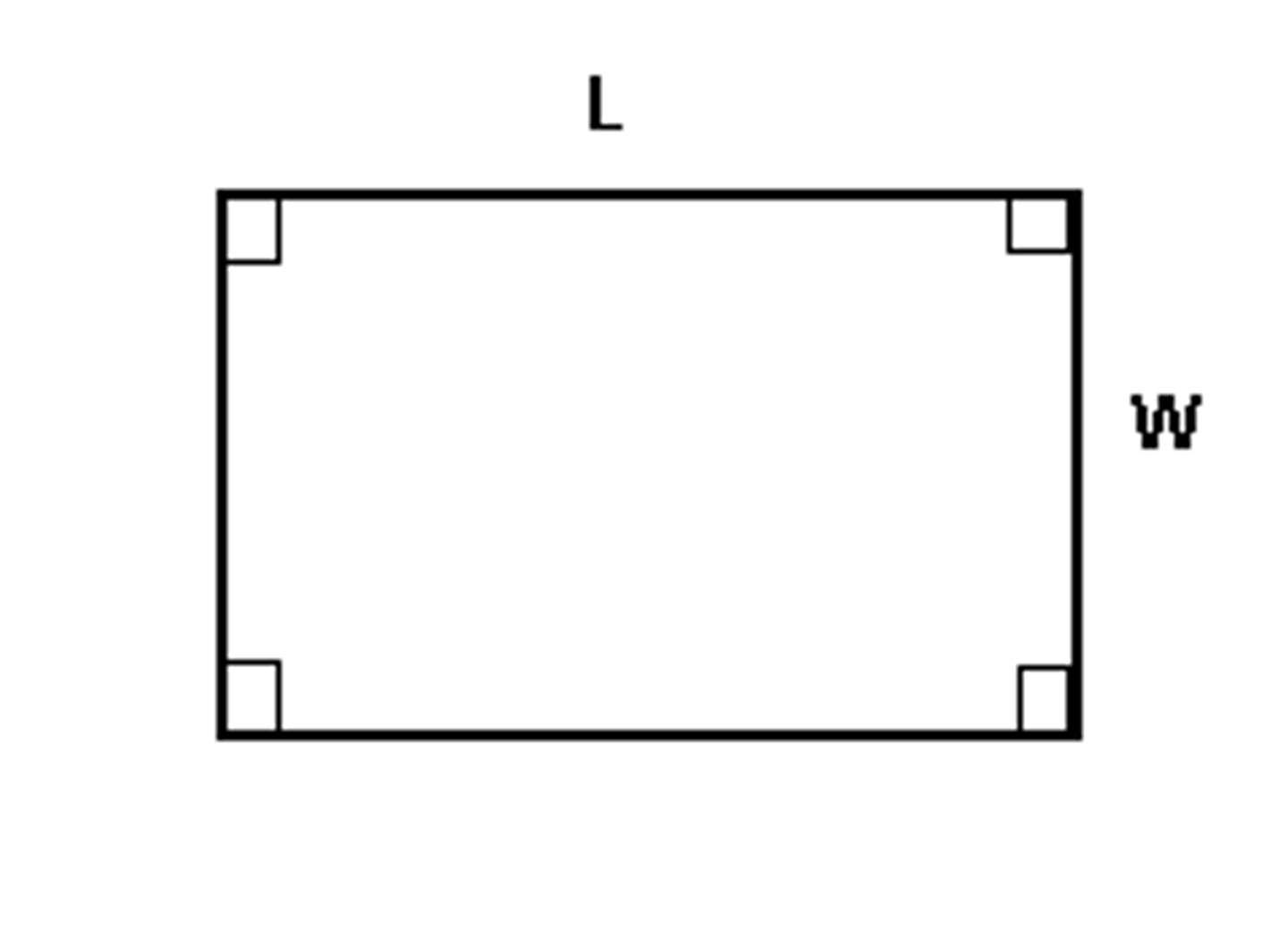
Perimeter of a Rectangle

P=2(length)+2(width)

P=2l+2w

Area of a Parallelogram

A=(base)(height) or A=bh

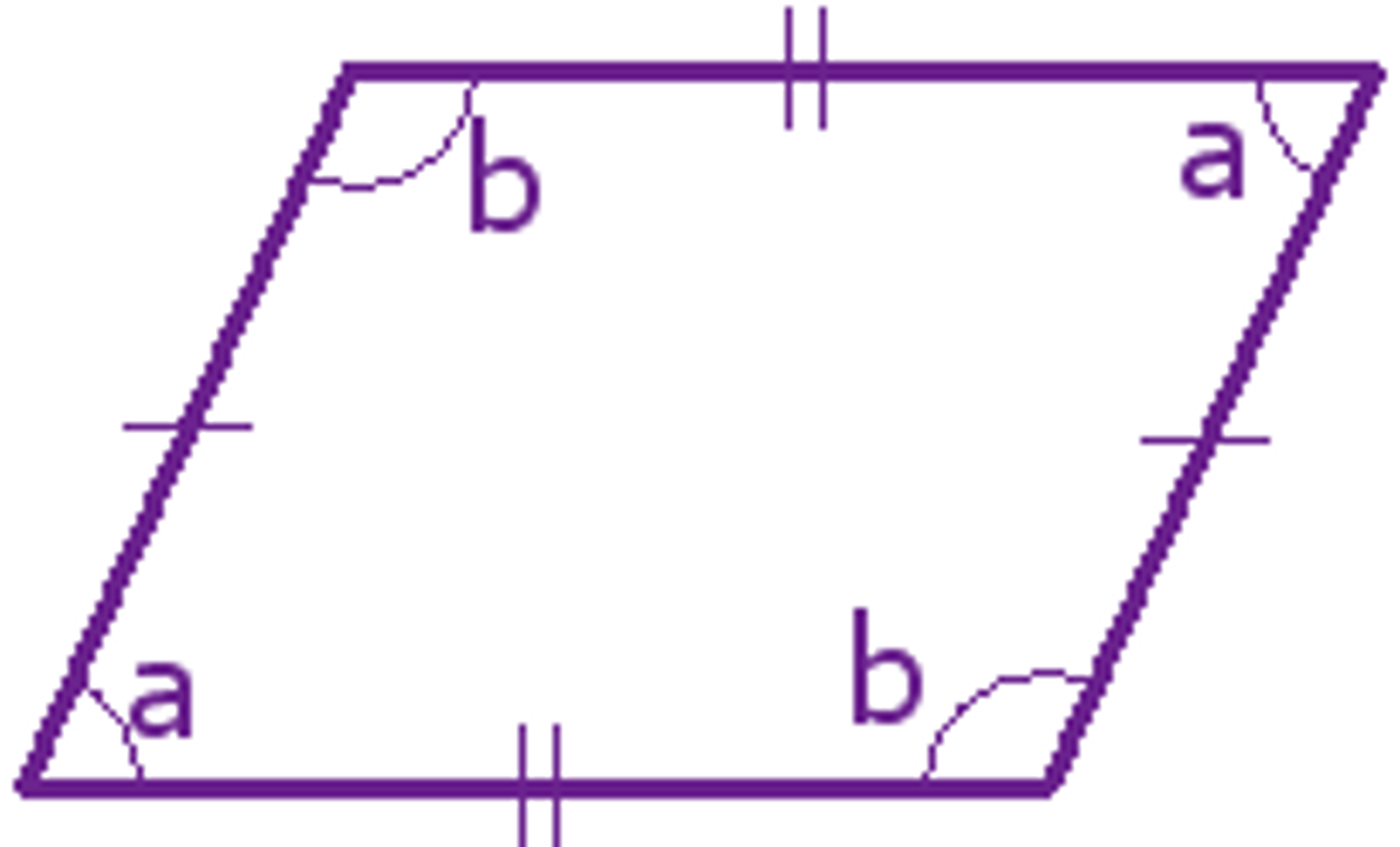
Angles in a Parallelogram

Opposite angles are equal.

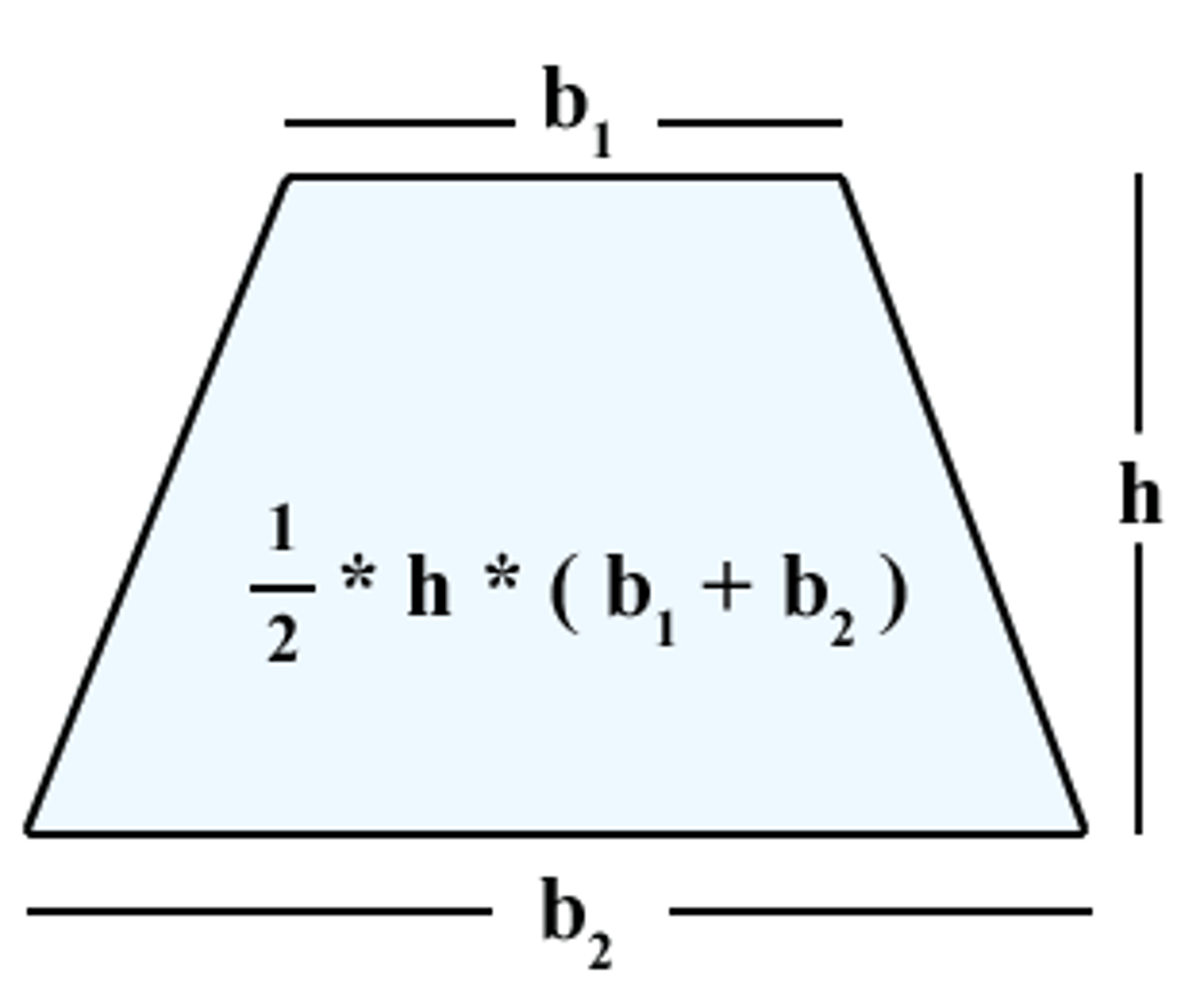
Area of a Trapezoid

A=½(h)(b₁+b₂)

Surface Area of a Sphere

SA=4πr²

Surface Area of a Cylinder

SA=2πr²+2πrh

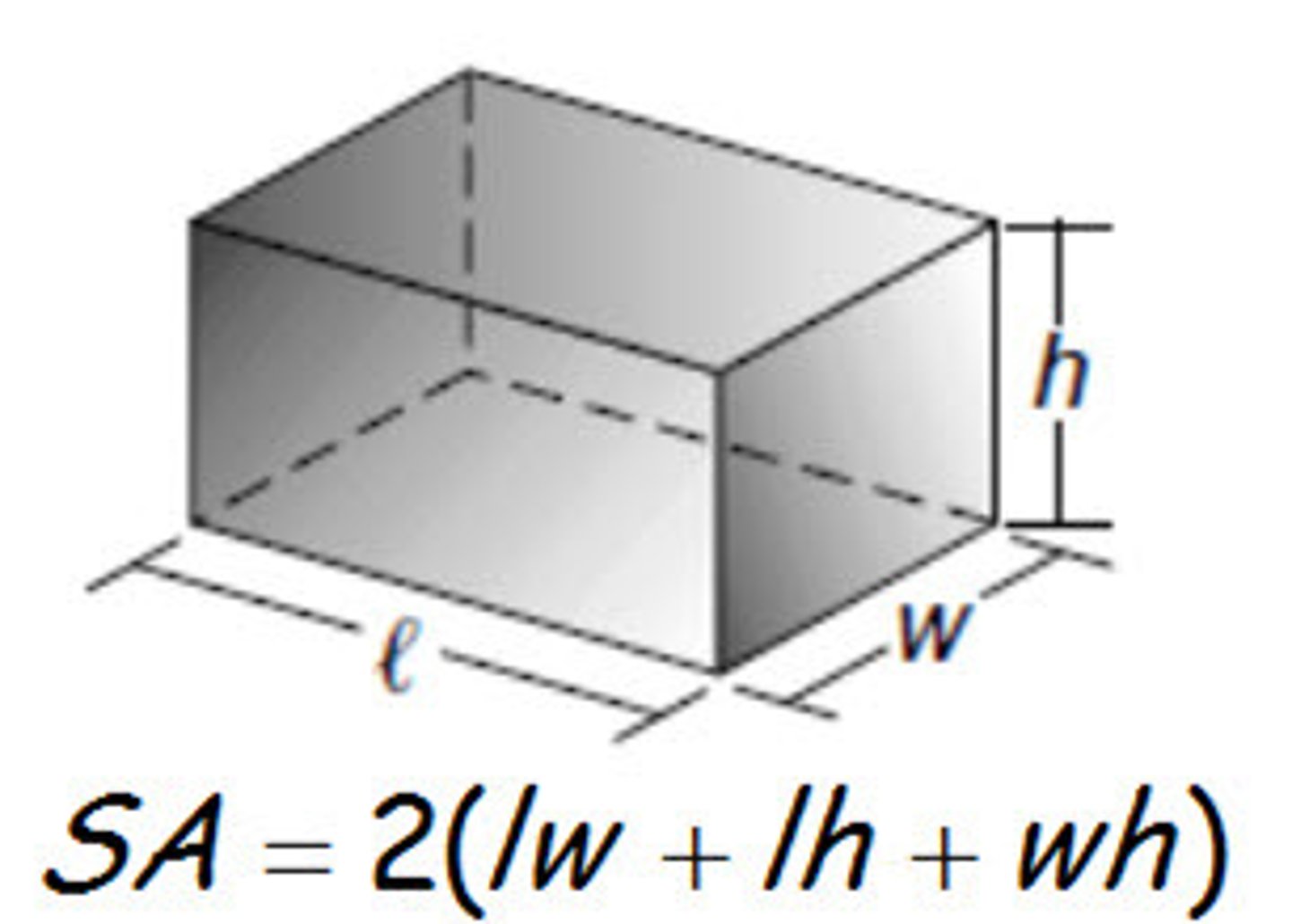
Surface Area of a Prism

SA=2(lw+lh+wh)

SA=2B+Ph, where B is the area of the base, P is the perimeter of the base, and h is the height of the prism.

Volume of a Sphere

V=(4/3)πr³

Volume of a Cube

V=side³

V=s³

Volume of a Cylinder

V=πr²h

Diagonal of a Cube

Diagonal = side√3

D=s√3

Volume of a Prism

V=lwh

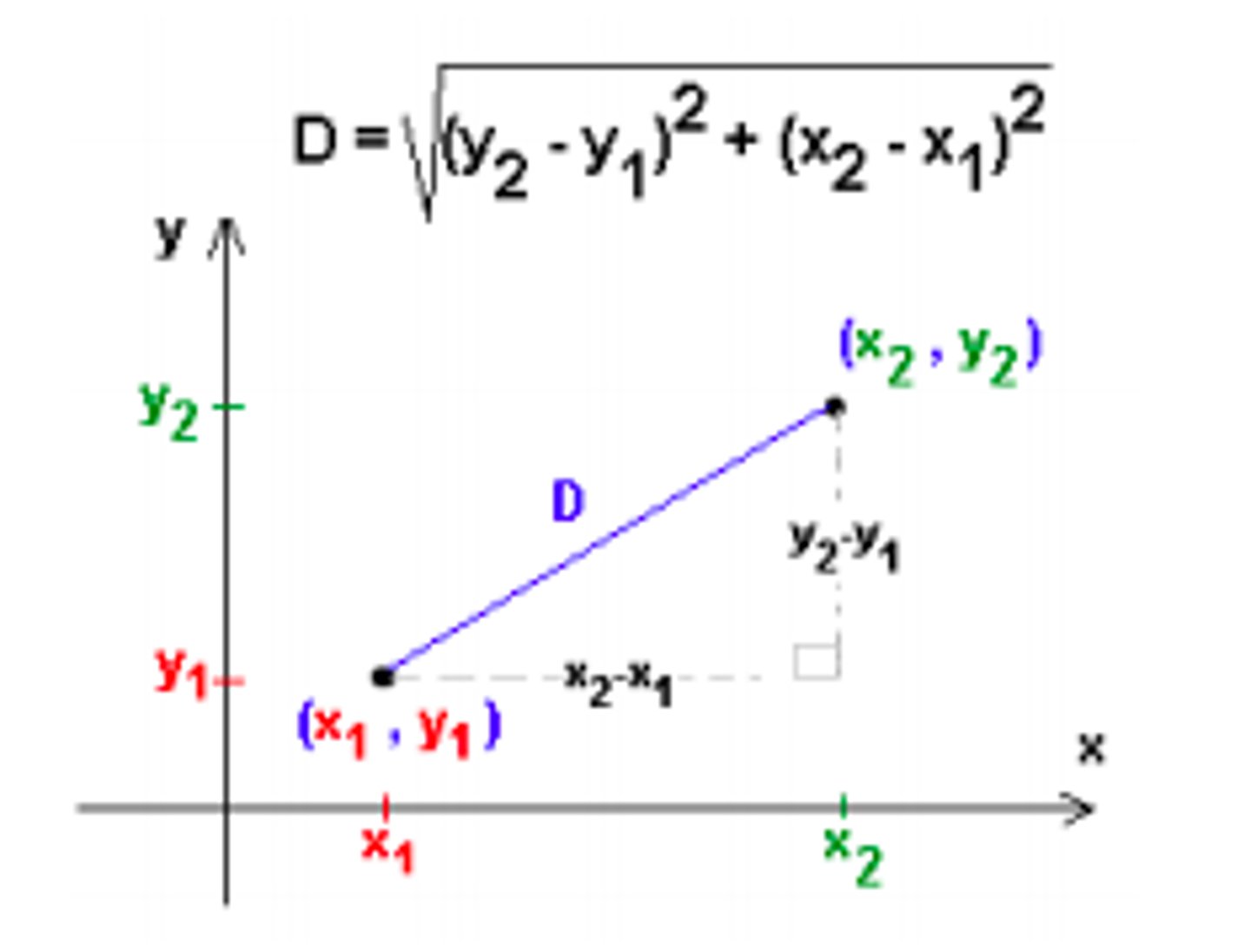
Distance Formula

(think Pythagorean theorem)

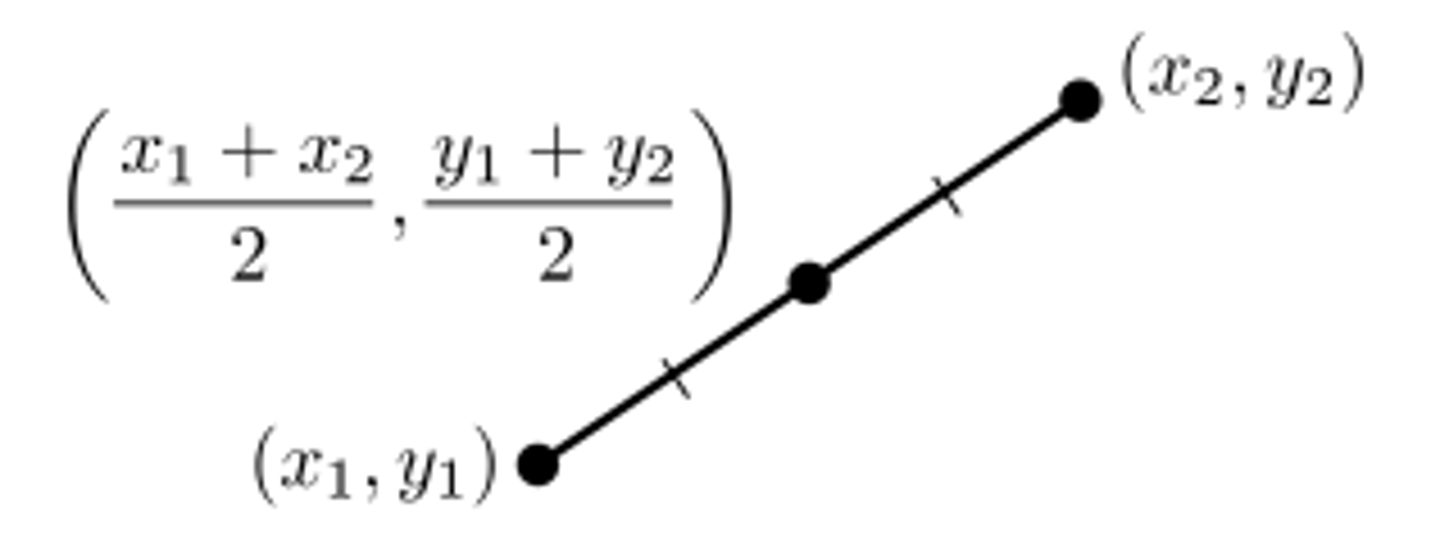
Midpoint Formula

Used to find the midpoint of a line

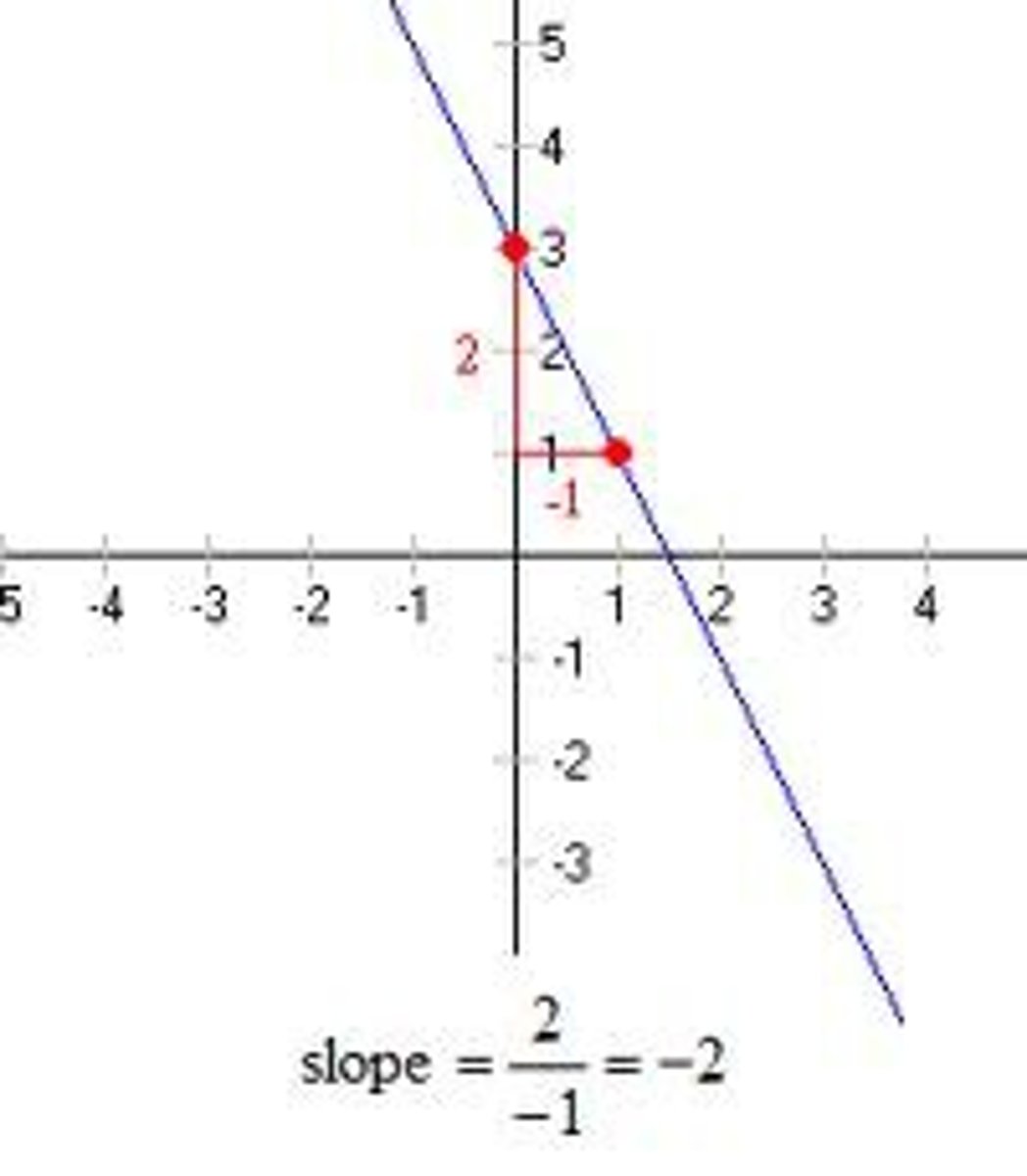
Slope

Rate of change of a line;

rise over run;

change in y /change in x

Parallel Lines

Same slope

Perpendicular Lines

Form 90 degree angles;

Slopes are negative reciprocals

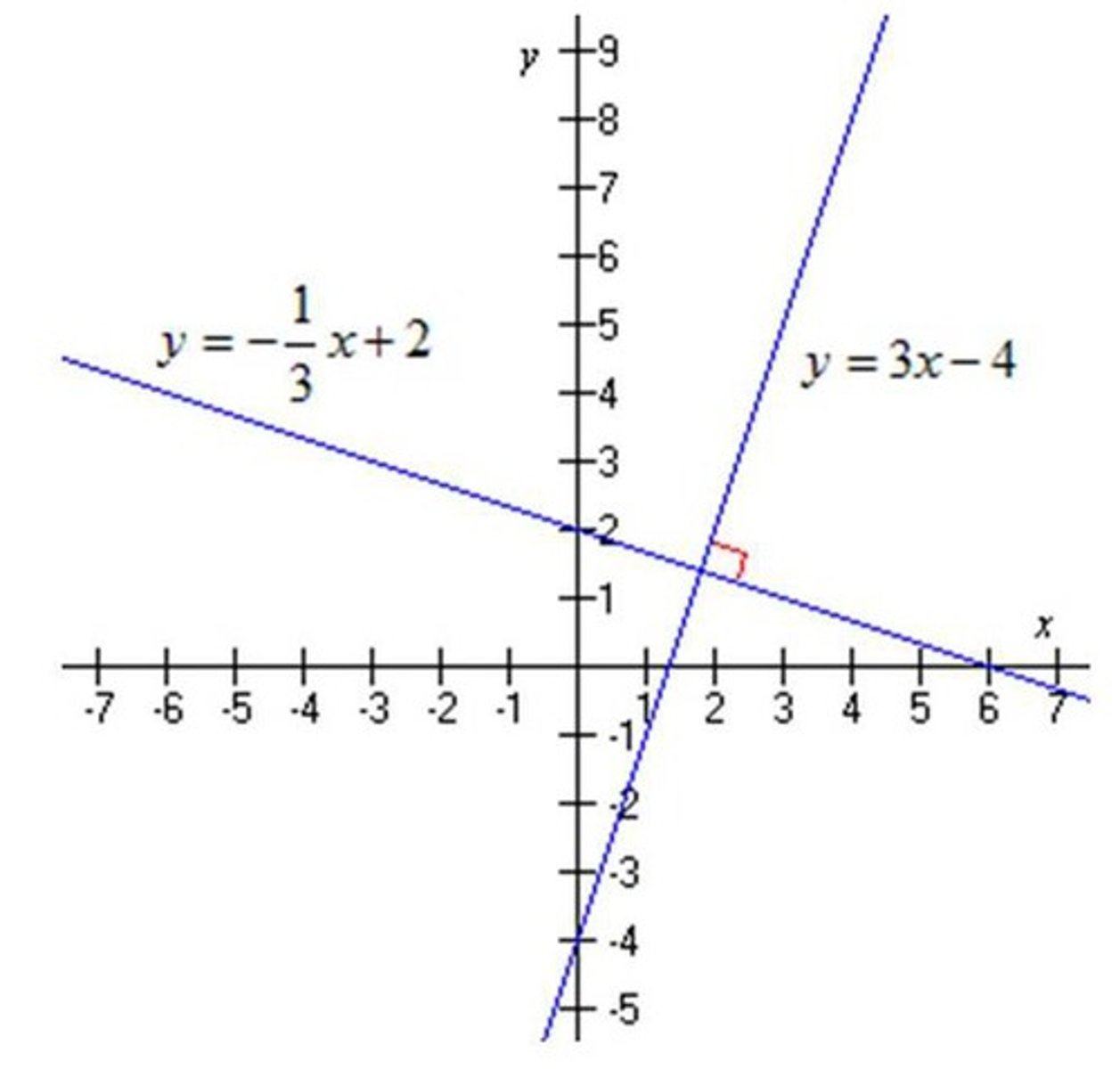
Horizontal Lines

slope = 0;

Defined by x=a, where a is a constant

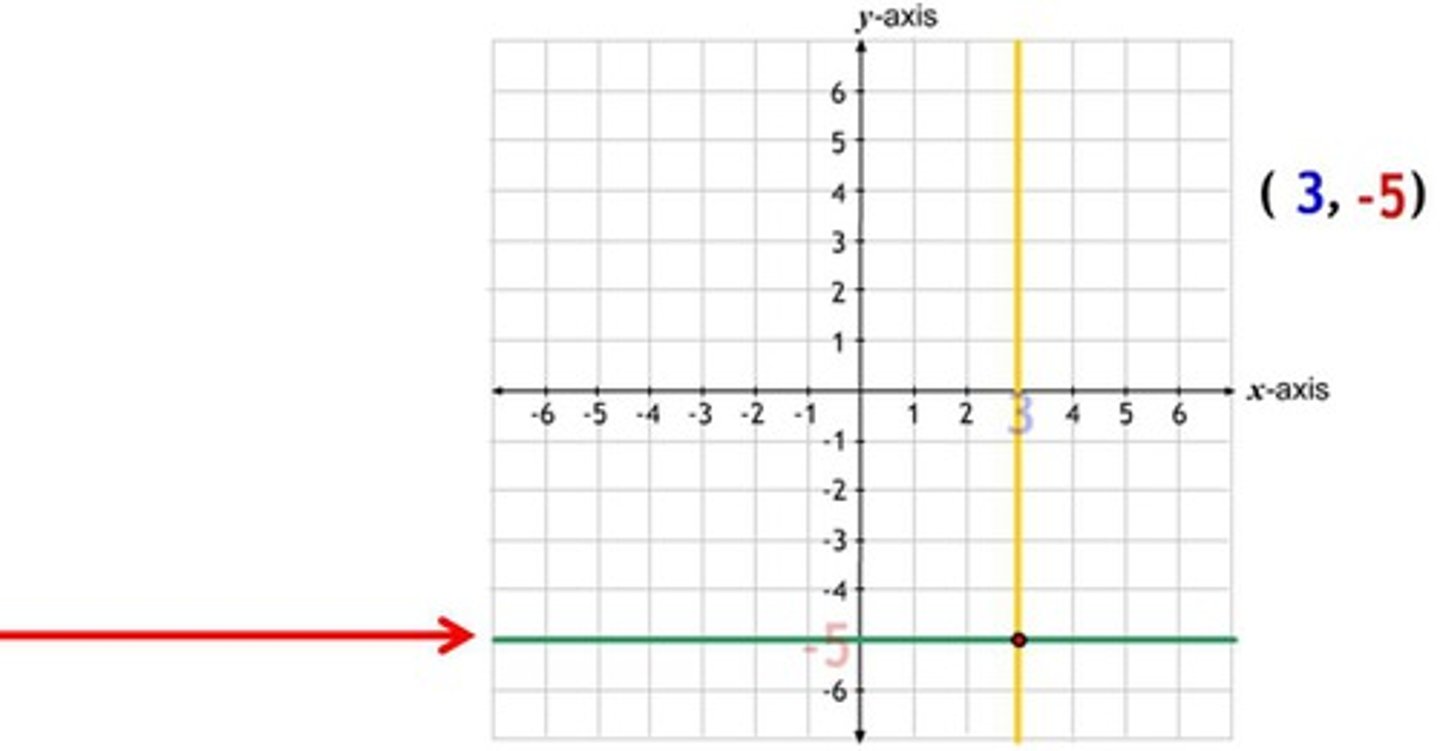
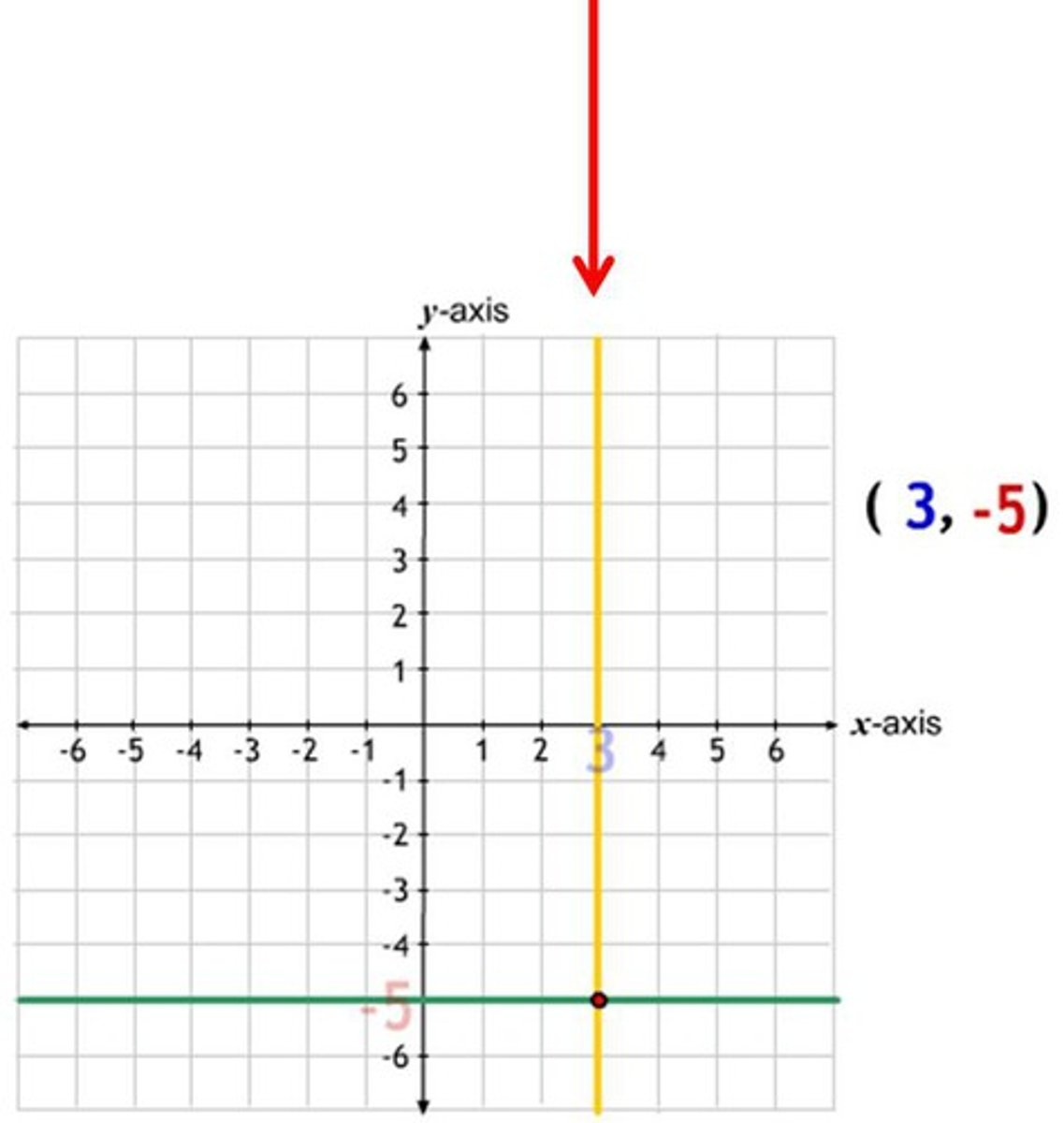
Vertical Lines

slope = undefined;

Defined by y=a, where a is a constant

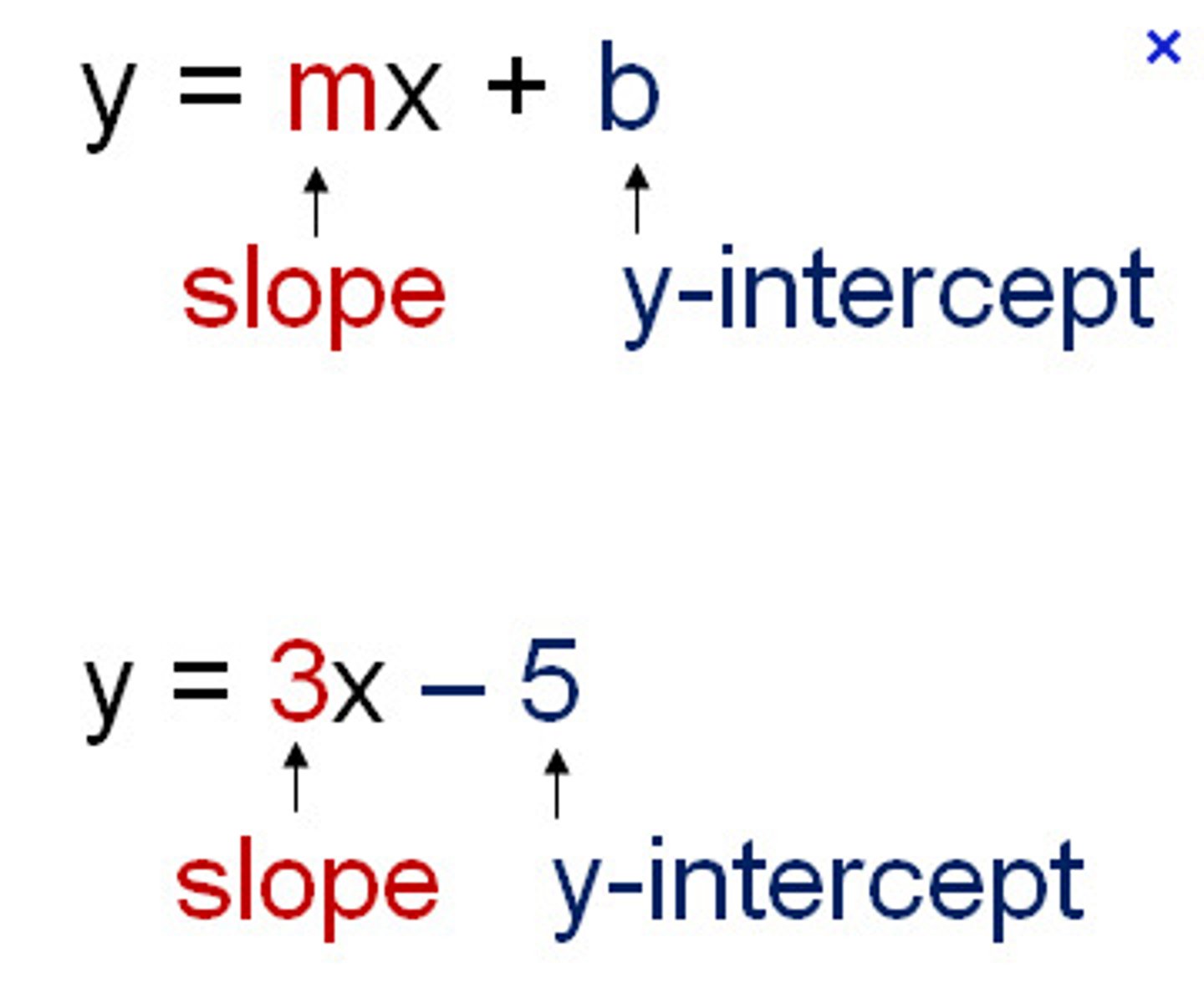
Slope-Intercept Formula

Use if you know the slope and the y-intercept

Point-Slope Formula

Use if you know the slope and a point on the line

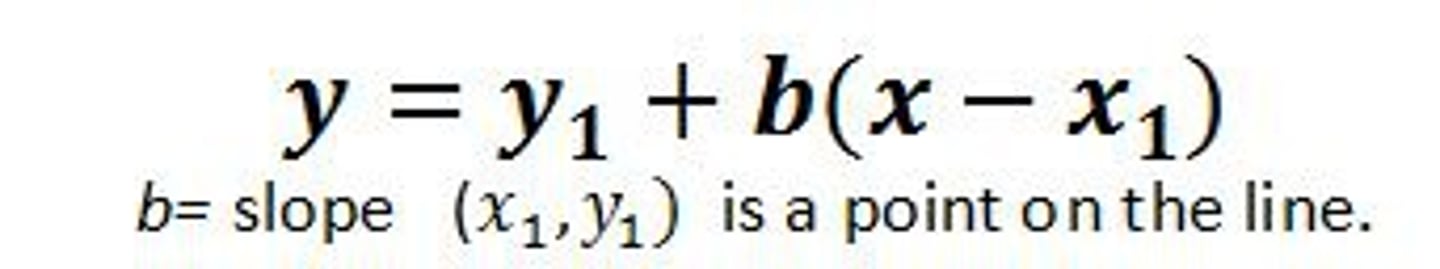
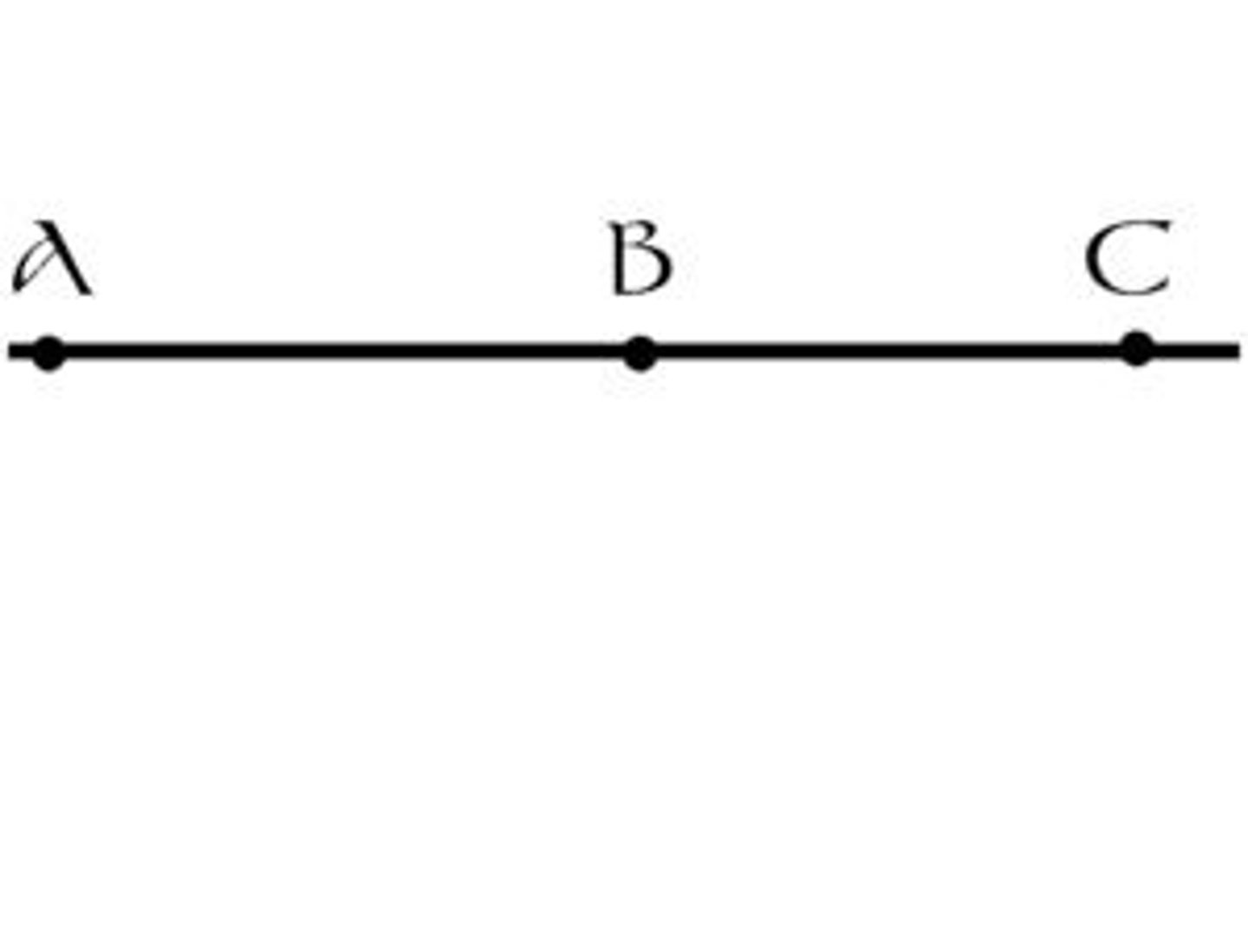
Collinear Points

A, B, and C are all collinear points

Average (Arithmetic Mean)

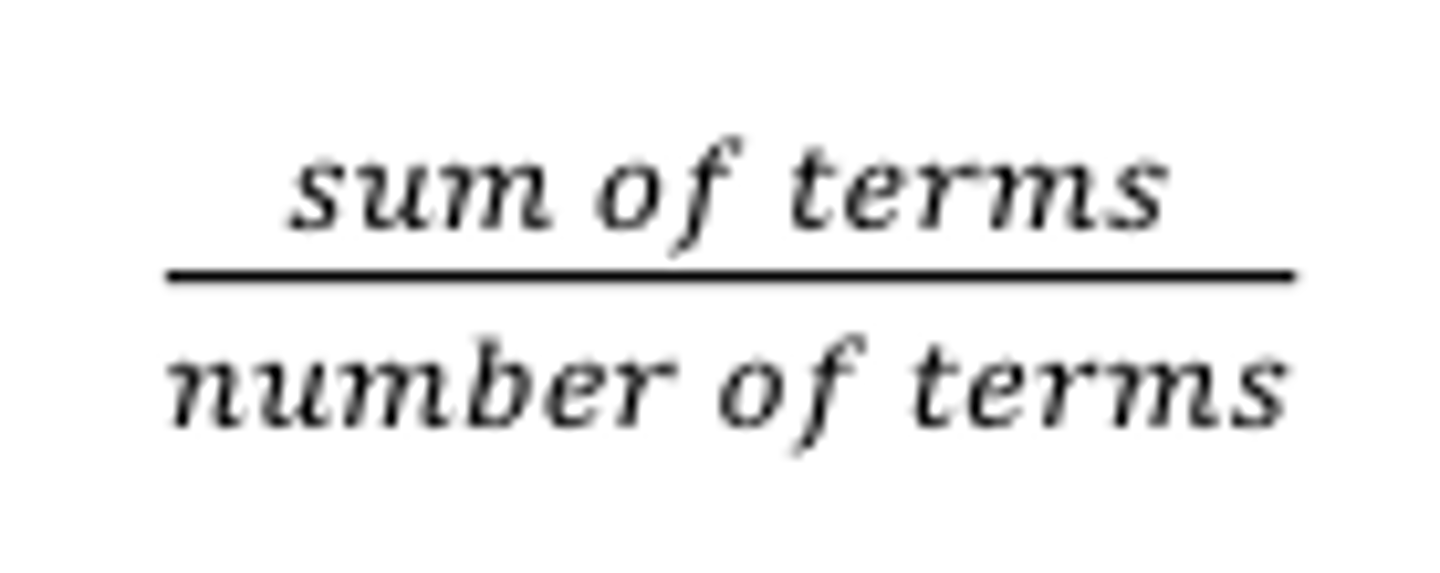
Average Speed

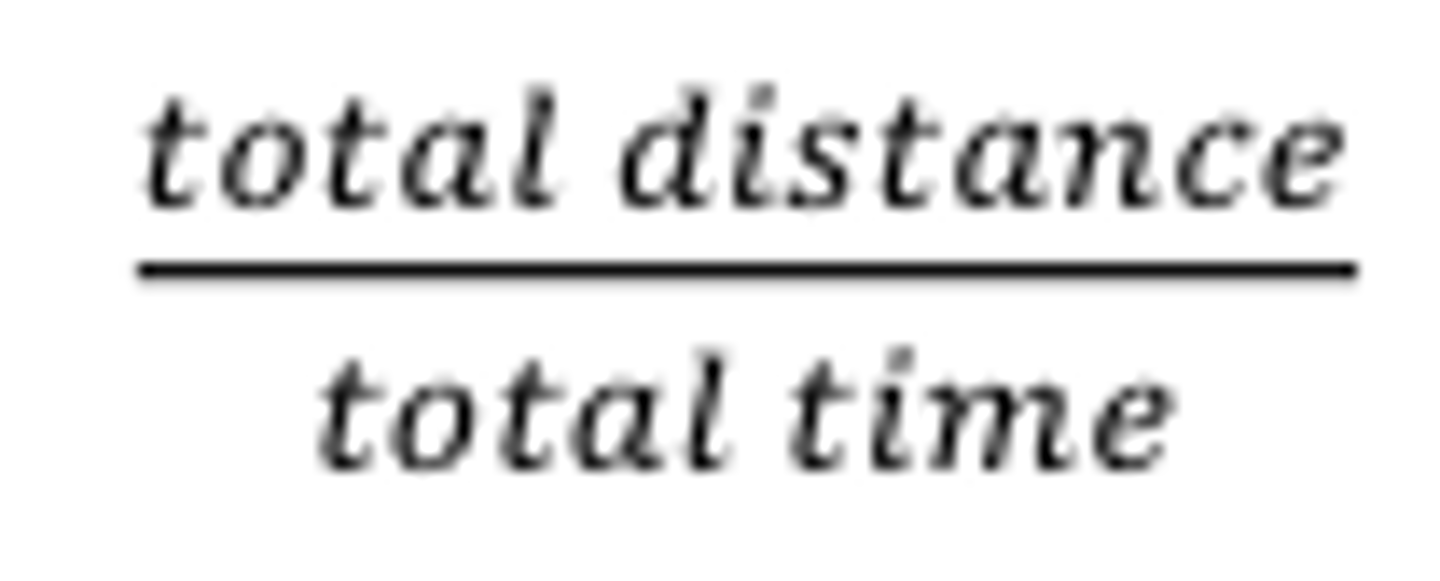
Weighted Average

Mode

Value(s) that occurs most frequently!

Median

Middle point of an ordered list!

Fundamental Counting Principle

If an event can happen m ways and another, independent event can happen n ways, then both events can happen in m ∗ n ways.

Probability

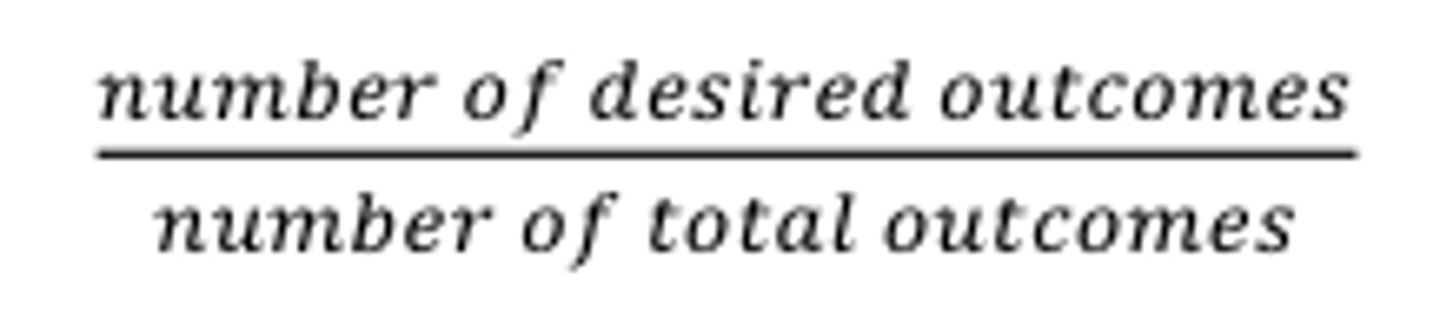
Probability of two independent events happening

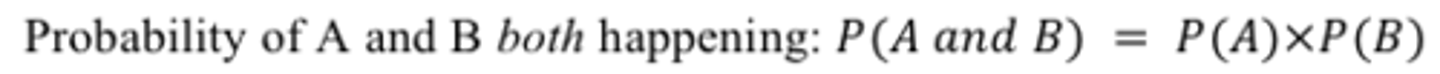
Ratios

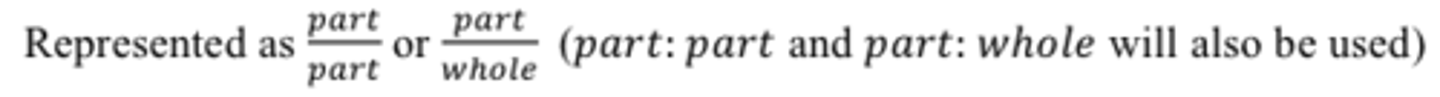
Absolute Value

The distance from 0 (an absolute value takes any number and makes it positive)!

Multiplying Variables with Exponents

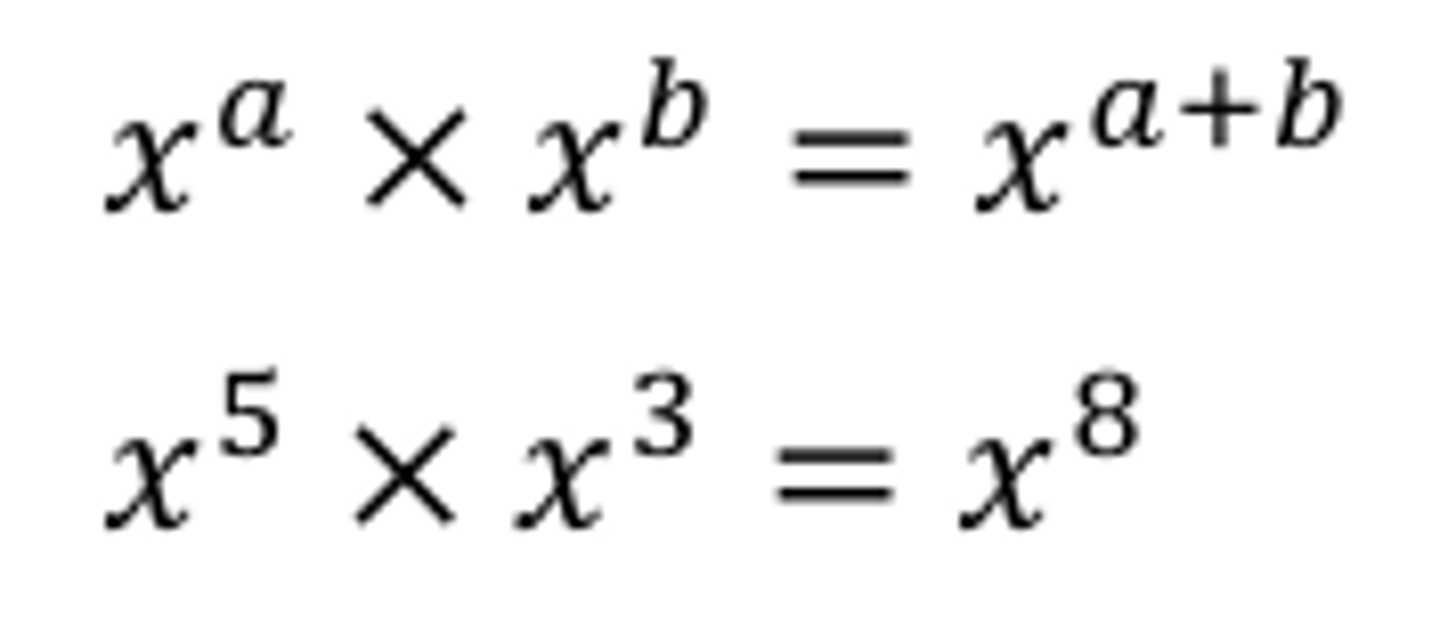
Dividing variables with exponents

Negative Exponents

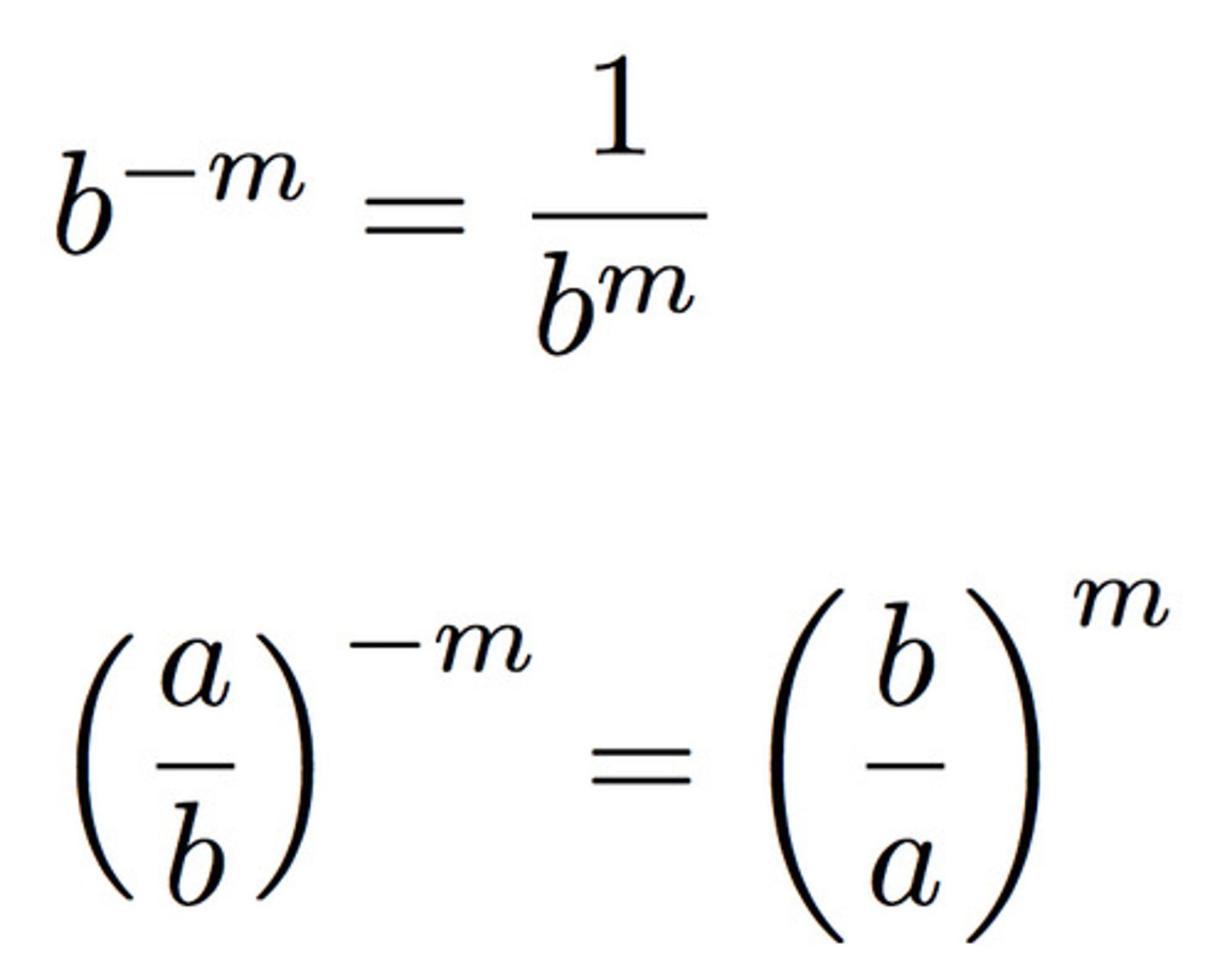
Two Exponents, one base

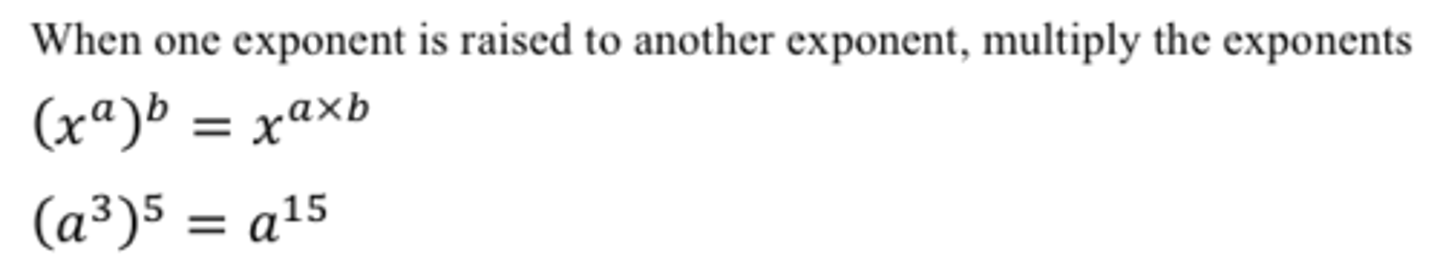
Distributive Property

Base raised to the power of 0

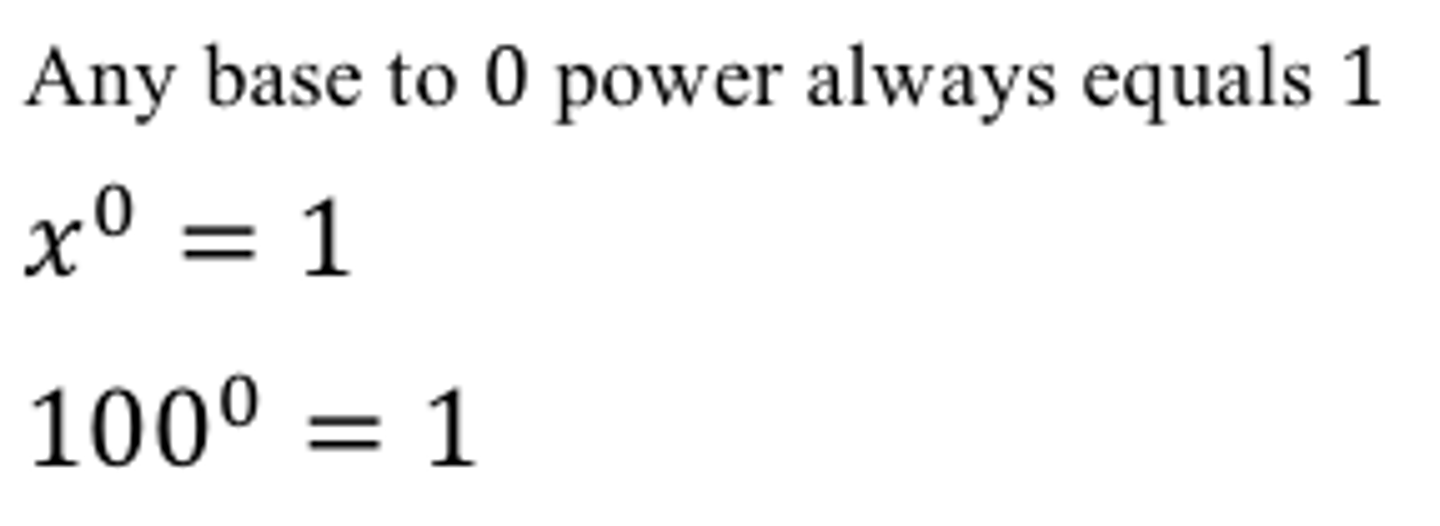
Fractional Exponents

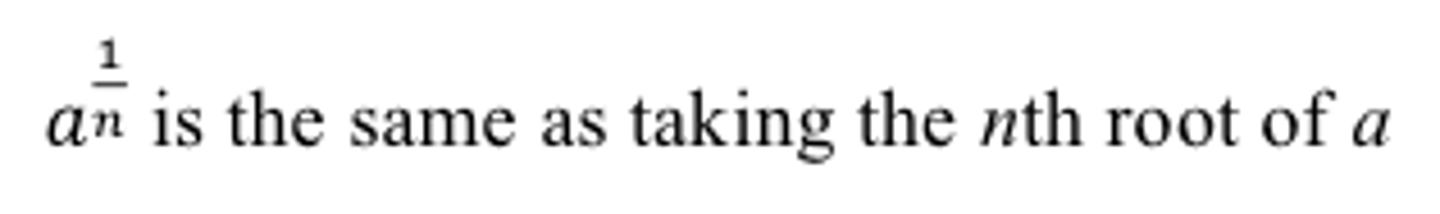
"FOIL"ing

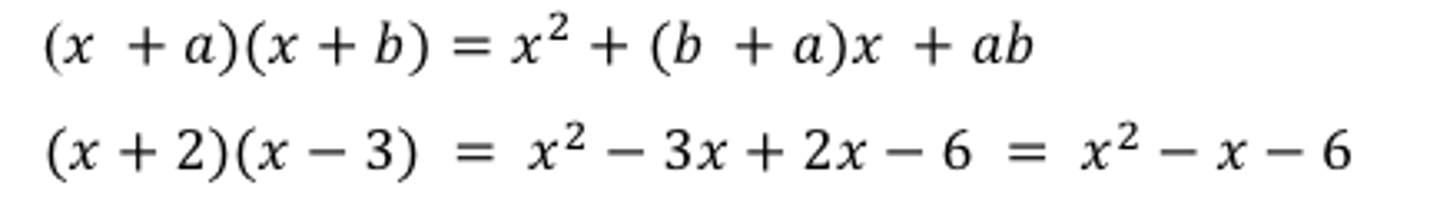
Difference of Squares

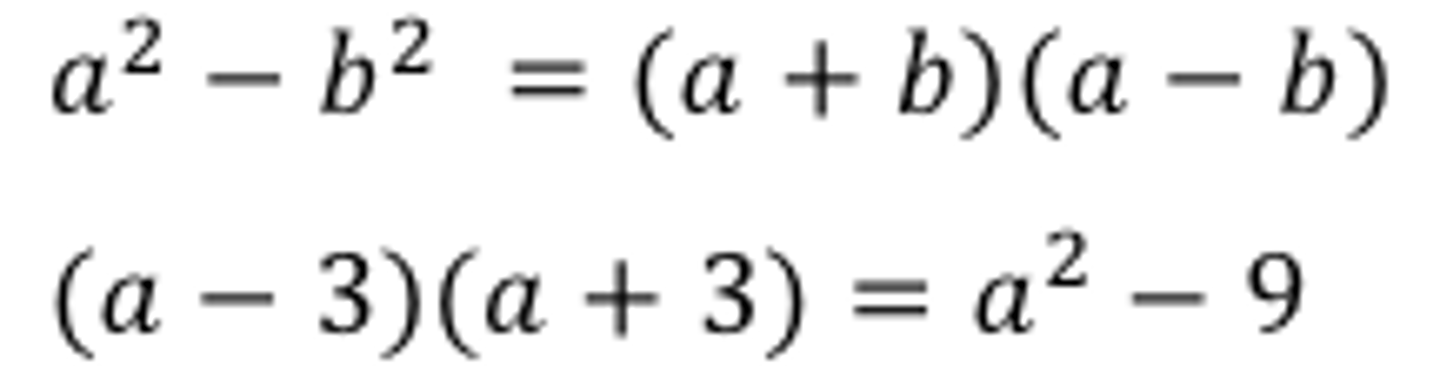
Perfect Square Trinomials

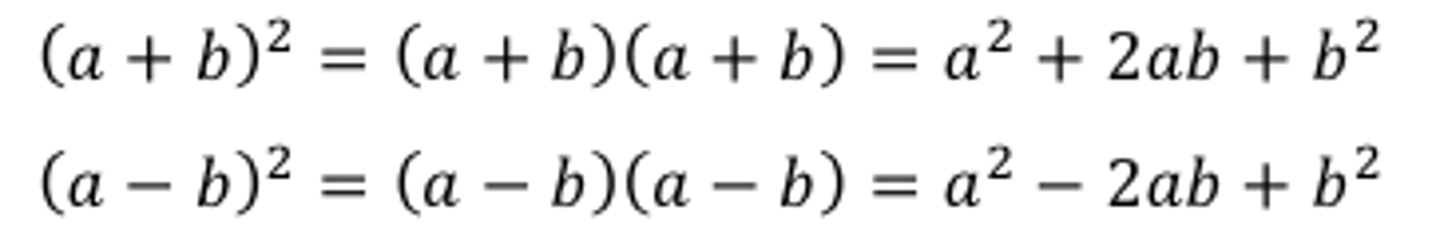
Function Transformations: Amplitude increase of f(x) in which all values of y are multiplied by 3. A vertical stretch.

3(f(x))

Function Transformations: Amplitude decrease of f(x) in which all values of y are multiplied by 0.5. A horizontal Stretch.

0.5(f(x))

Horizontal Shift Right (ie: 3 units right)

y = f(x-3)

Horizontal Shift Left (ie: 3 units left)

y = f(x+3)

Vertical Shift up (ie: shift 2 units up)

y = f(x) + 2

Vertical Shift Down (ie: shift 2 units down)

y = f(x) - 2

Matrix Addition

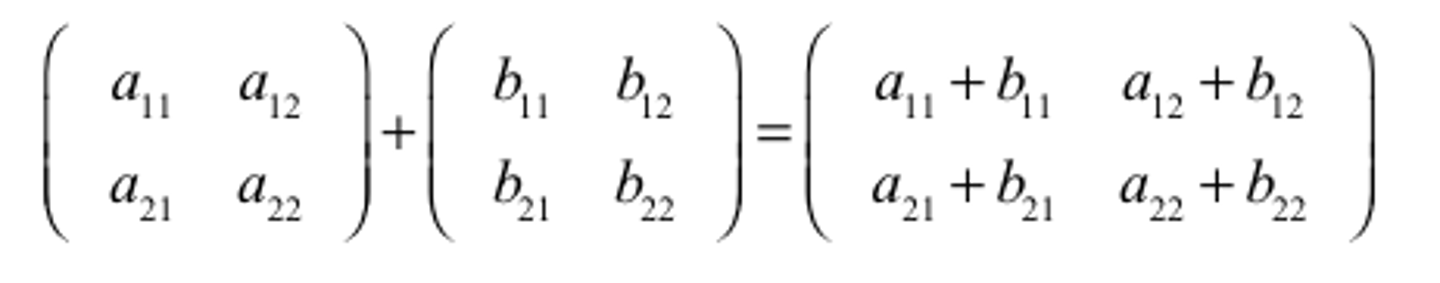
Matrix Multiplication

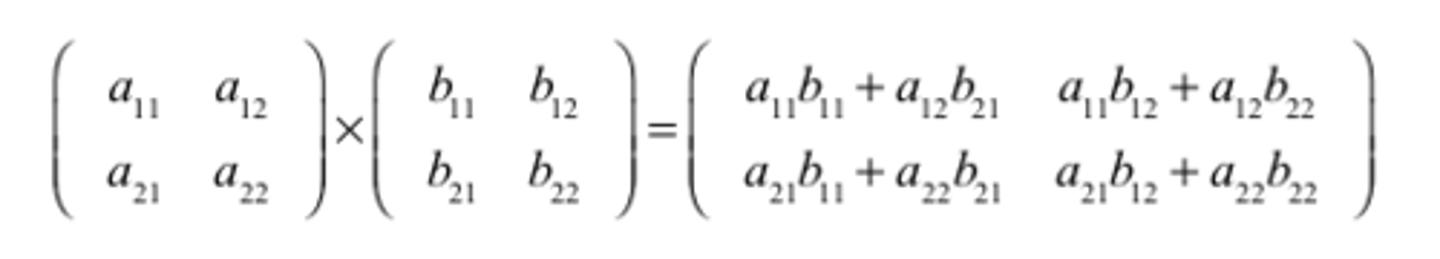
Rewriting logarithms as exponentials

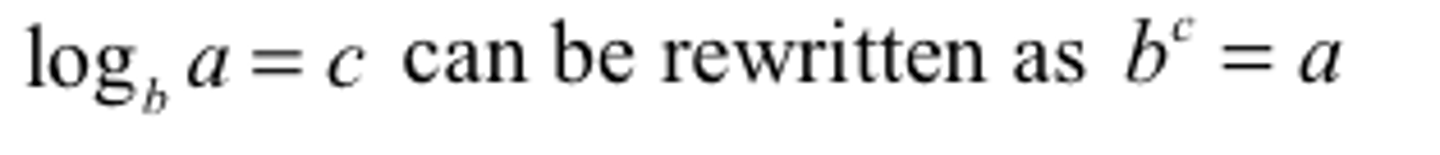
Logarithm Power Rule

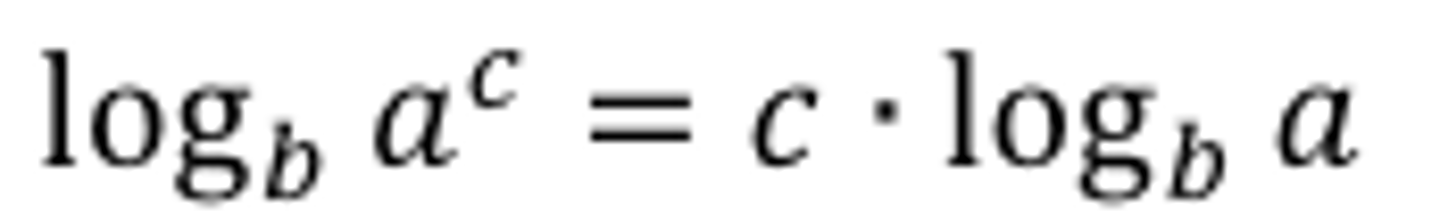
Logarithm Product Property

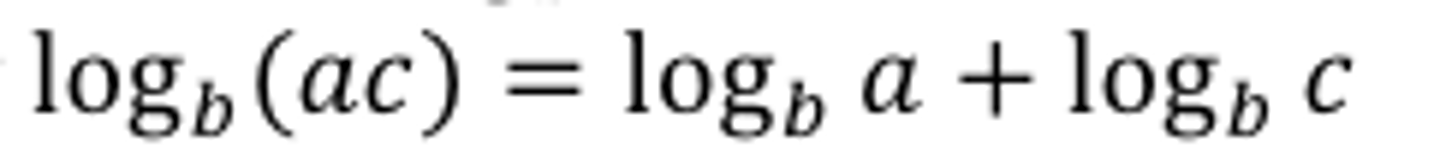
Logarithm Quotient Property

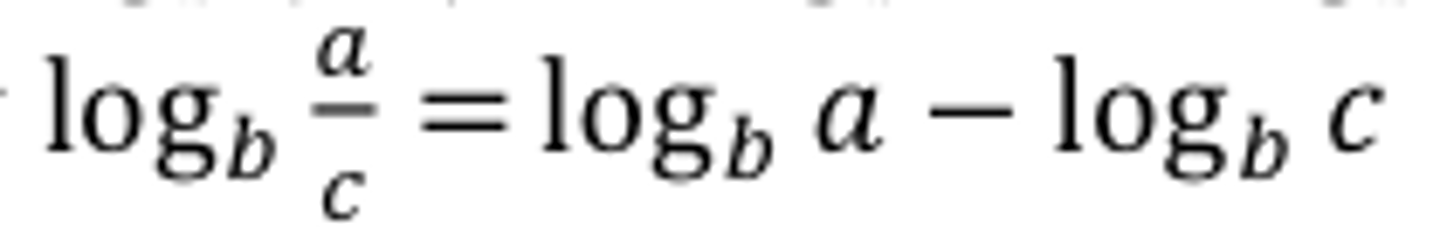
Complex number i

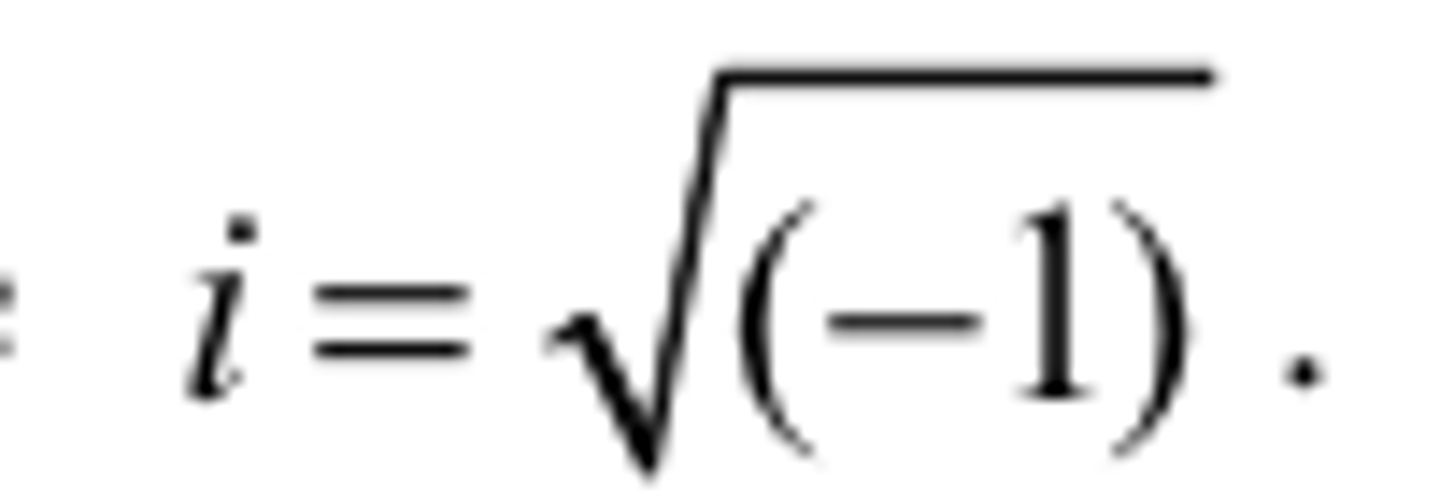
Powers of i

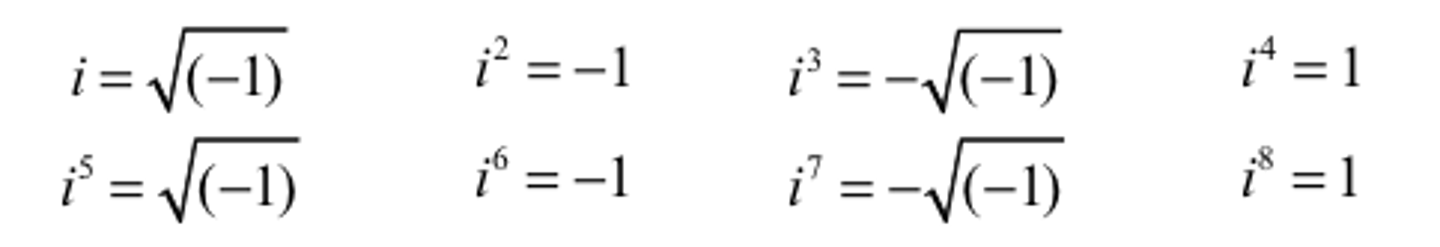
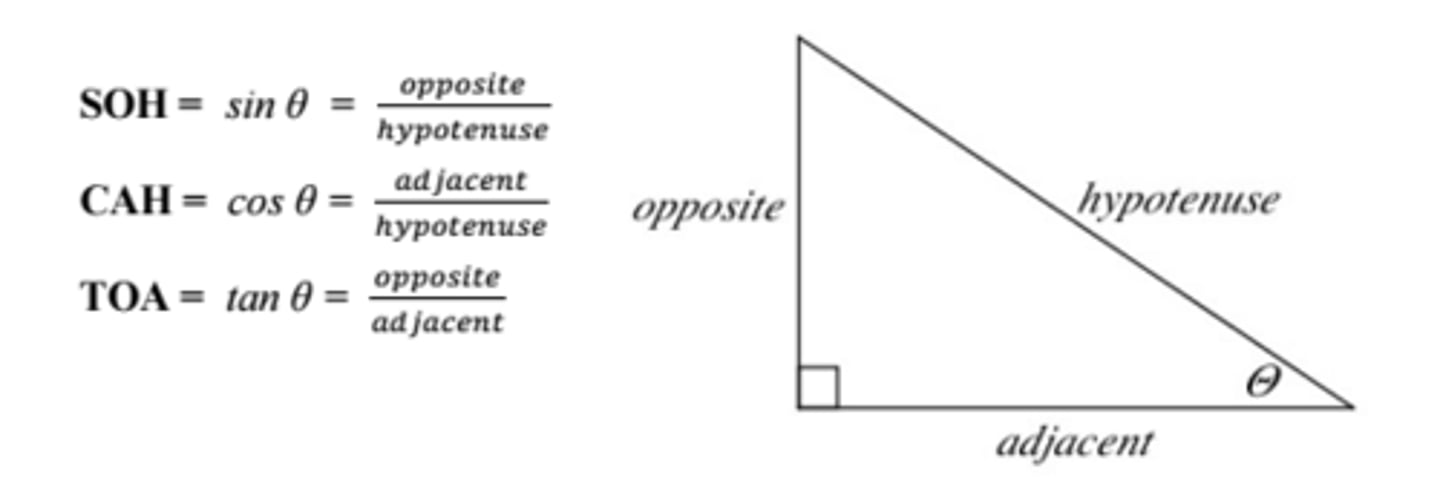
SOH-CAH-TOA

Trigonometric Identities

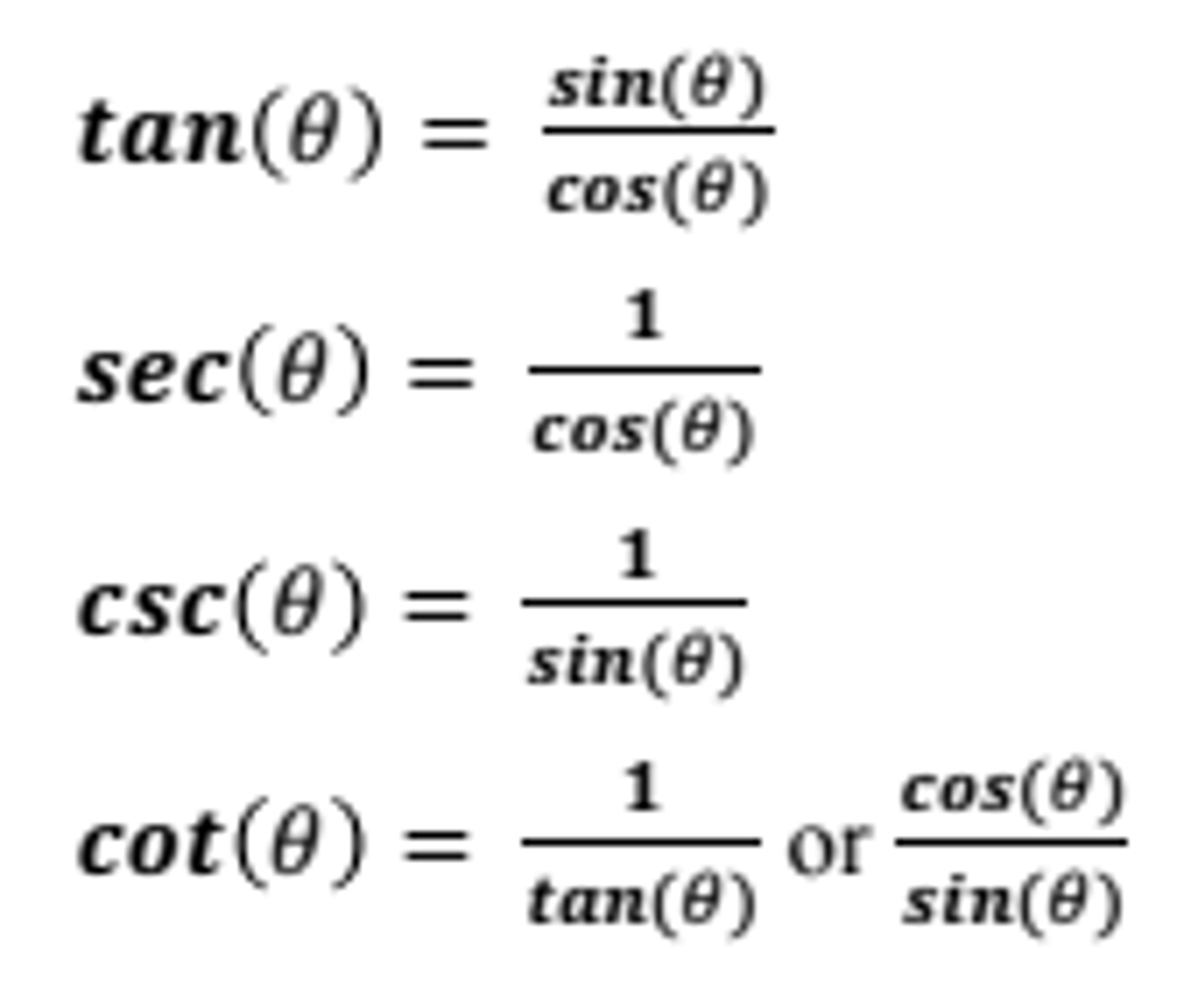
Pythagorean Identities

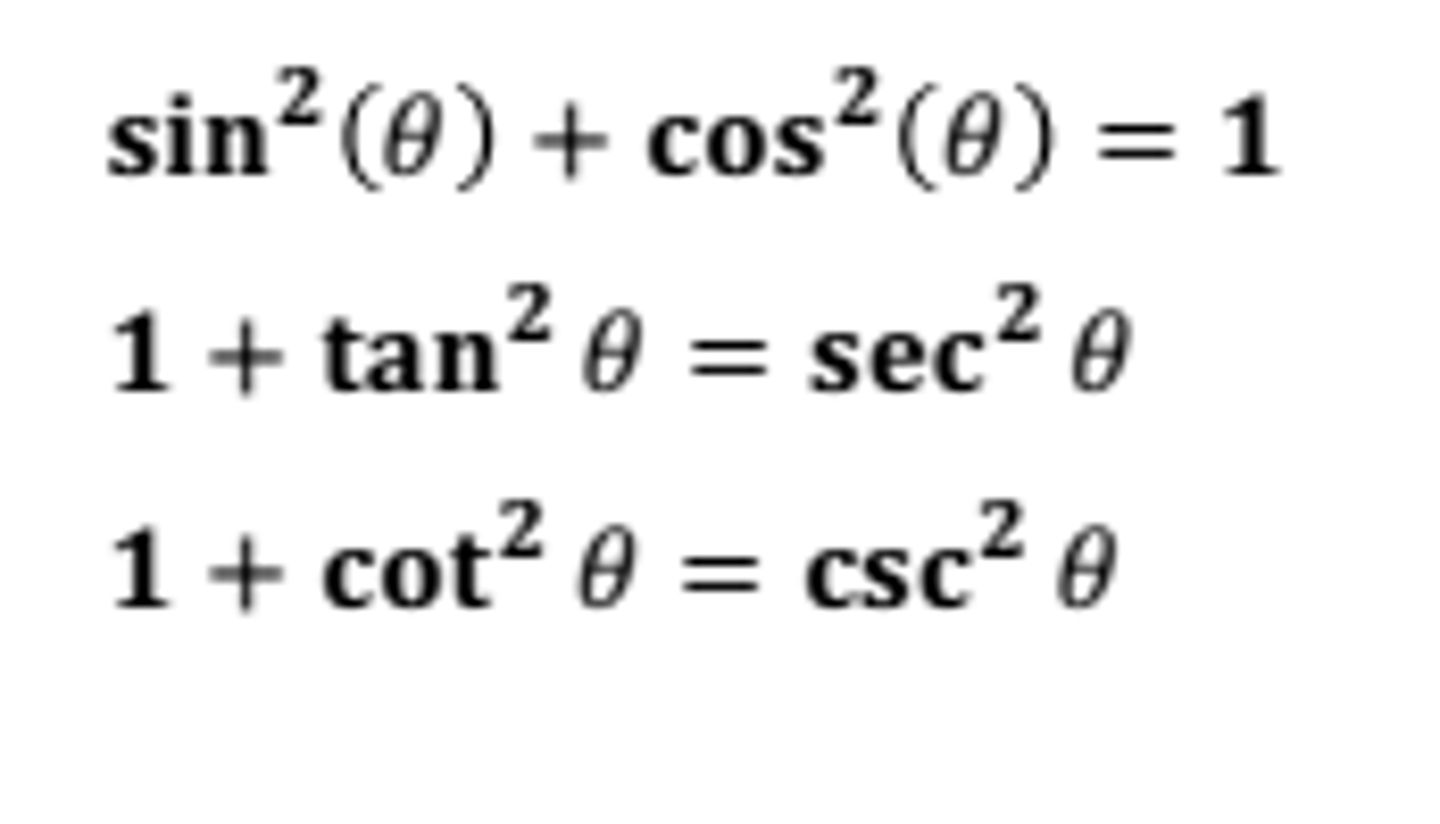
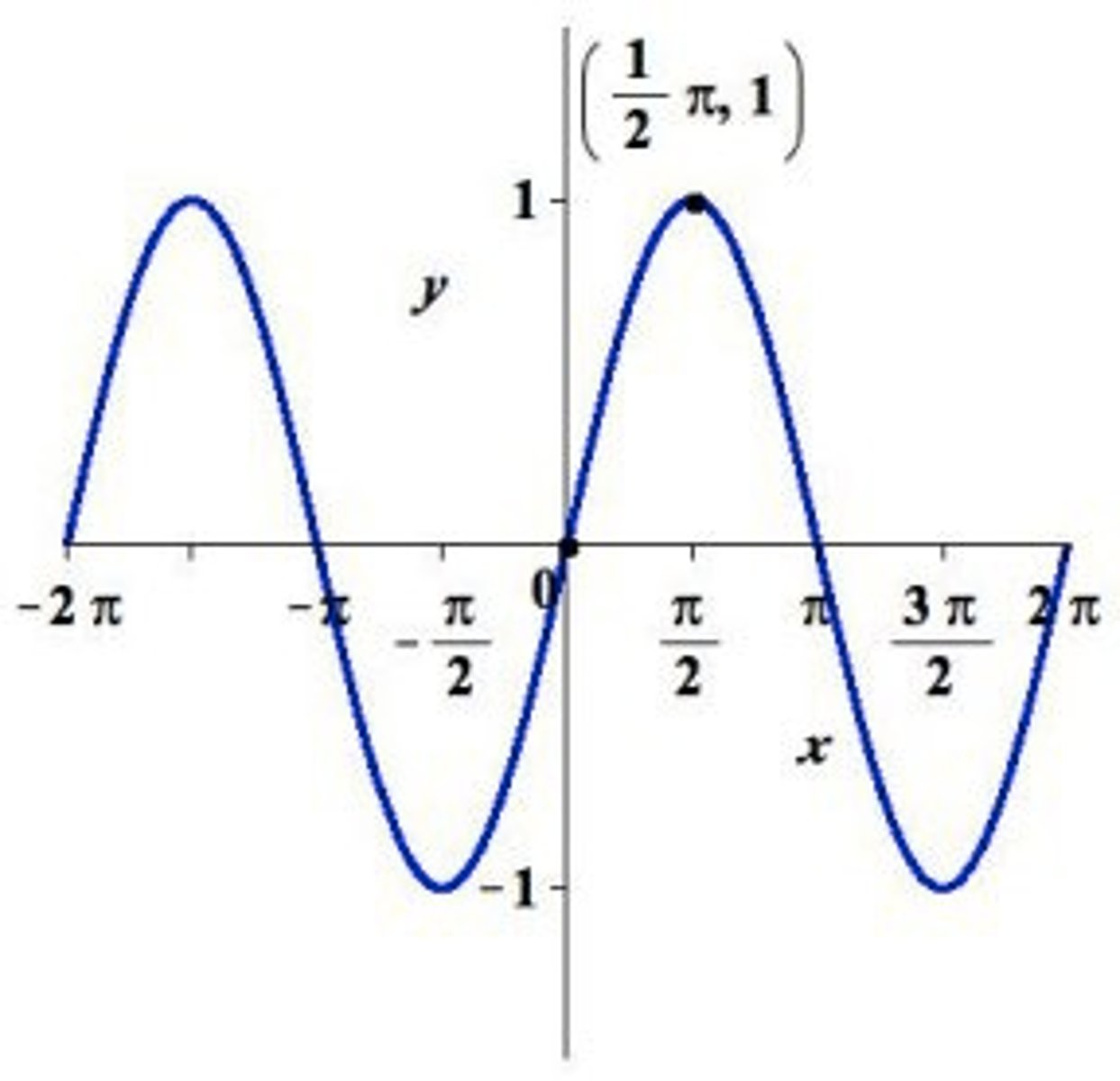
Graph of y = sin(x)

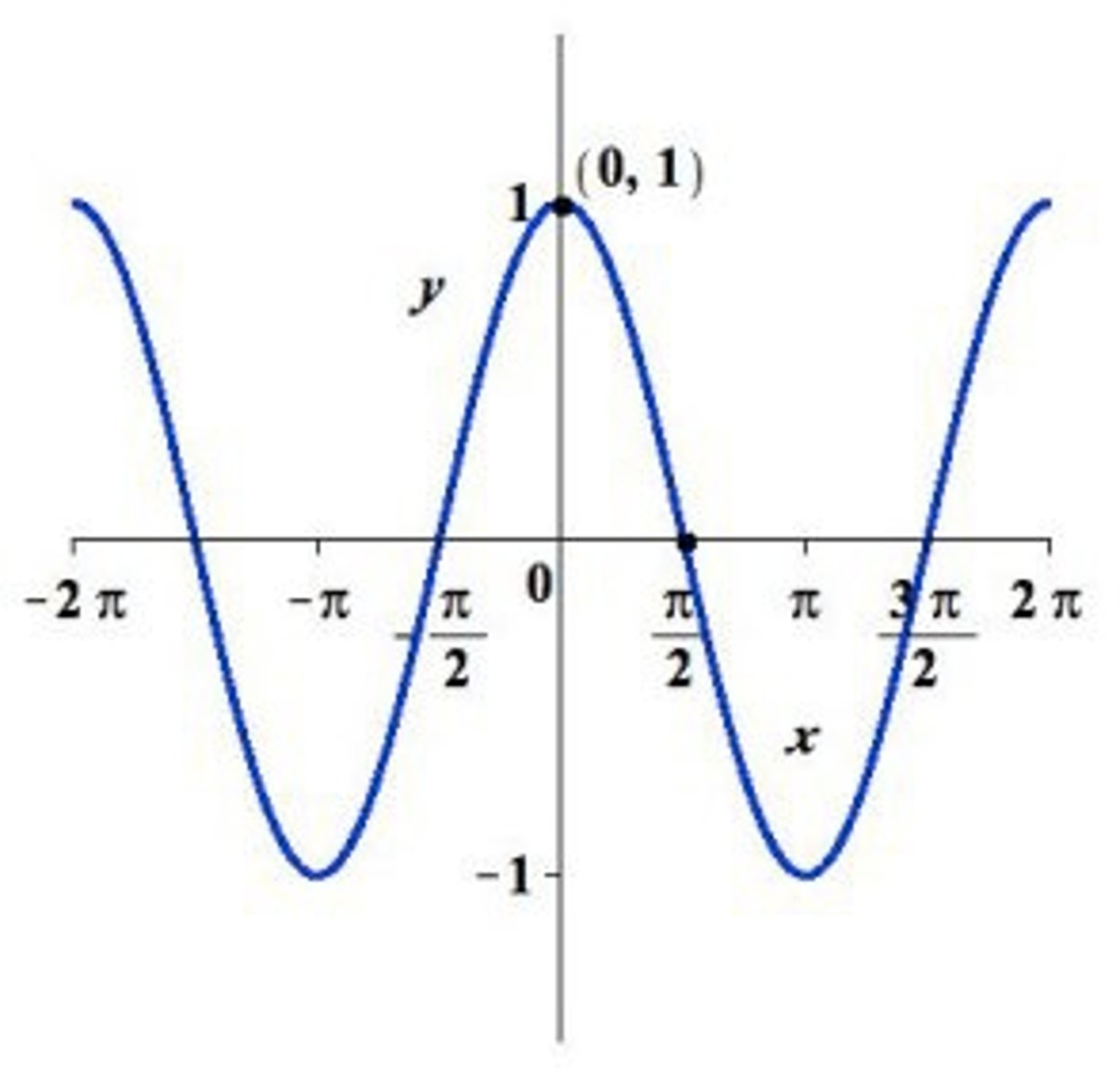
Graph of y = cos(x)

Graph of y = tan(x)

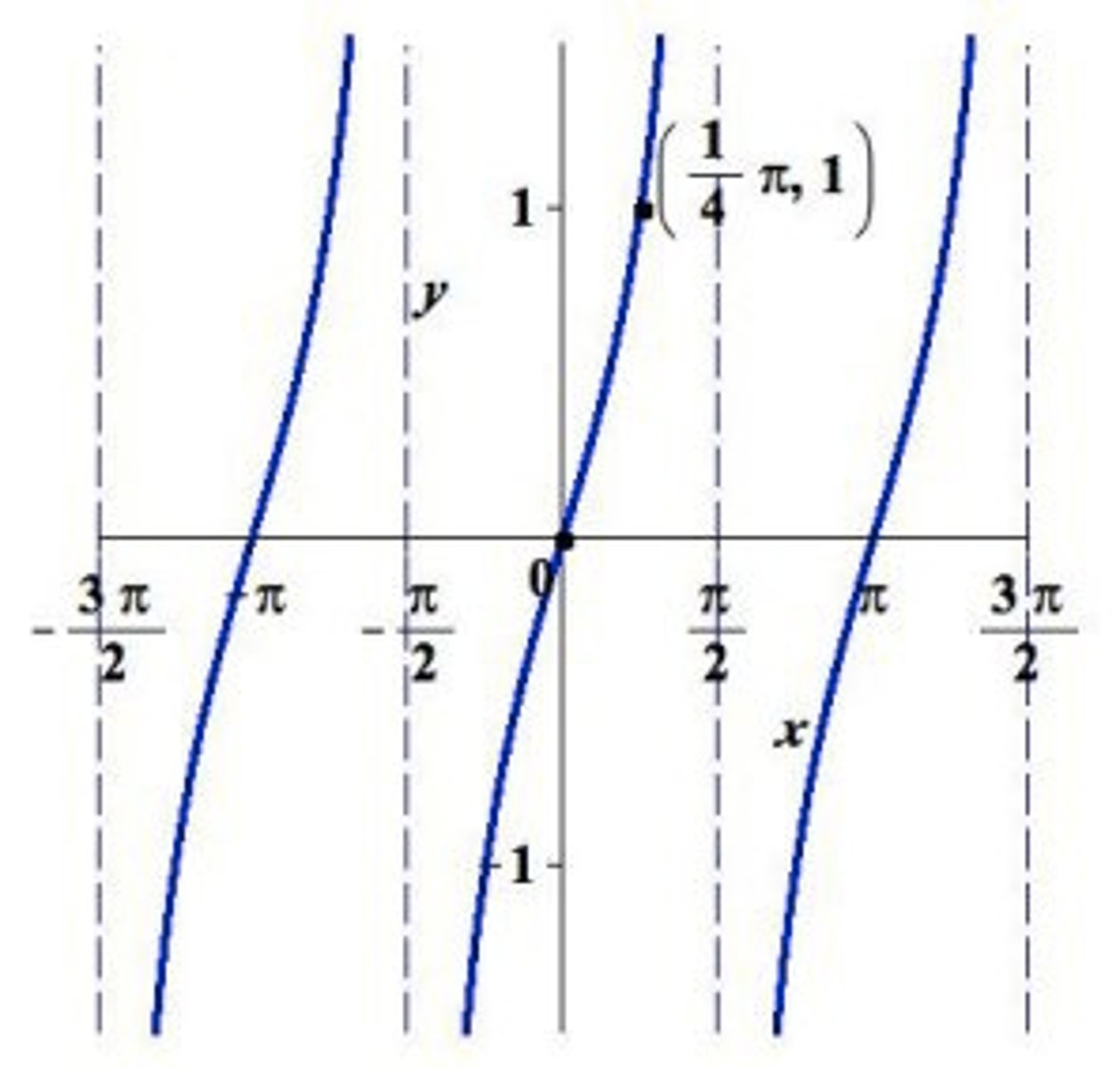
Graphing Trigonometric Functions

y = Asin(Bx - C) + D

Integers

Any number that is not a decimal or a fraction. ie: -30, 1, 2, 50

Whole Number

Any number that is not a negative or a fraction. ie: 0, 2, 37, 455

Odd Integer

Any integer that cannot be divided by 2 without a remainder.

ie: −111, −57, −1, 1, 67!

Even Integer

Any integer that can be divided by 2 without a remainder (including zero!)

ie: 2, 20, -30

Consecutive Integers

Numbers that directly follow each other on a number line.

ie: −4,−3,−2,−1... or 3,4,5,6...

variable form: n, n+1, n+2, n+3

Consecutive Odd Integers

Odd numbers that follow each other on a number line.

ie: −5,−3,−1,1...

variable form: n, n+2, n+4