A1 - Kinematics

Important terms:

• distance (d, x, r, y, z) - how far travelled in any direction measured in meters (m)

• speed (v) - how fast travelled in any direction measured in meters per second ($ms^-1$)

  • formula for speed:$distance/time$

• instantaneous speed (v) - the speed at a specific distance measured in meters per second ($ms^-1$)

• average speed (v) - the speed over a total distance measured in meters per second ($ms^-1$)

• displacement (s) - distance in a specific direction measured in meters (m)

• velocity (v) - speed in a specific direction measured in meters per second ($ms^-1$)

• acceleration (a) - change in speed over time measured in meters per second squared ($ms^-2$)

  • formula for acceleration:$velocity/time$

Vectors are measurements that have magnitude and direction whereas scalars are measurements with only magnitude. Therefore, distance and speed are both scalars and acceleration, velocity and displacement are vectors.

Equations of Uniform Motion (SUVAT):

• there are 4 kinematic equations (known as SUVAT) that can describe any object moving with constant or uniform acceleration.

  • s = displacement

  • u = initial velocity (at t=0)

  • v = final velocity

  • a = acceleration

  • t = time interval

• the four kinematic (SUVAT) equations are

  • $v=u+at$

  • $s=ut+(1/2)at²$

  • $v²=u²+2as$

  • $s=((v+u)/2)t$

We can make many assumptions about the nature of one or more of the SUVAT components based on the wording of the question:

• if the question says “starts from rest” or does not mention the initial velocity, u and t can be assumed to equal zero

• if the object is at its maximum height, v must equal zero

• if the object is falling (or being thrown upwards) a is equal to g, therefore meaning its value must be 9.81 (or -9.81)

Projectile Motion:

The trajectory of an object undergoing projectile motion consists of two components, a vertical component and a horizontal component. We must evaluate these two components separately.

Key things to remember are:

• the acceleration due to gravity is g and is downwards and constant throughout the motion

• the horizontal velocity V_v is constant and in the direction of the object throughout the motion

• the vertical velocity V changes in direction and magnitude throughout the motion e.g. at the top V_v=0

Graphs:

displacement-time graph:

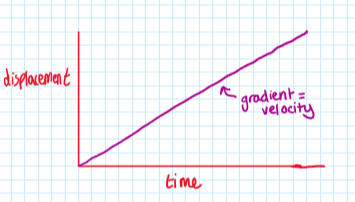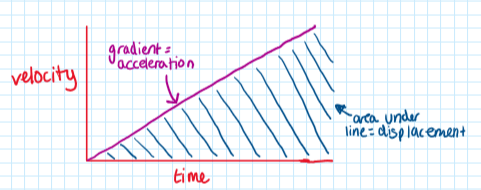
velocity-time graph:

A2 - Forces and Motion

Newton’s First Law:

Newton’s first law of motion states:

a body will remain at rest or move with constant velocity unless acted on by a resultant force

If the resultant force acting on an object is zero, it is said to be in translational equilibrium. Therefore, the body must either be at rest or moving at a constant velocity.

Newton’s Second Law:

Newton’s second law of motion states:

the resultant force on an object is directly proportional to its acceleration

We can also write this as: $F=ma$

• F= resultant force (N)

• m = mass (kg)

• a = acceleration ($ms^-2$)

This means that objects will accelerate if there is a resultant force acting upon them.

Newton’s Third Law:

Newton’s third law of motion states:

every action has an equal and opposite reaction

Forces arise in pairs, therefore if object A exerts a force on object B, then object B exerts an equal and opposite force on object A. A Newton’s third law force pair must be the same type of force, the same magnitude, opposite in direction and on different objects.

Contact Forces:

A contact force is defined as:

a force which acts between objects that are physically touching

Examples of contact forces include:

• friction - a force that opposes motion and occurs when objects rub against one another

  • static friction occurs when a body is stationary on a surface and is equal to Ff<µsFn

    • Ff = surface frictional force (N)

    • µs = coefficient of static friction (between 0 or 1 but not one of those numbers)

    • Fn = normal reaction force (N)

  • dynamic friction occurs when a body is in motion on a surface and is equal to $Ff=µdFn$

    • Ff = surface frictional force (N)

    • µd = coefficient of dynamic friction

    • Fn = normal reaction force (N)

• air resistance - a type of friction that occurs when an object moves through air

• tension - a force that pulls two objects connected by a length of something (often string or rope) and occurs when a force is applied to the length

• normal/reaction force - a component of the contact force acting perpendicular to the surface that counteracts the body and occurs when an object is supported by a surface

Non-Contact Forces:

A non-contact force is defined as:

a force which acts at a distance, without any contact between bodies, due to the action of a field

Examples of non-contact forces include:

• gravitational force - an attractive force experienced by two objects with mass in a gravitational field

• electrostatic force - a force experienced by charged objects in an electric field which can be attractive or repulsive

• magnetic force - a force experienced between magnetic poles in a magnetic field that can be attractive or repulsive

Hooke’s Law:

Hooke’s Law states that:

the extension of the material is directly proportional to the applied force (load) up to the limit of proportionality

This is represented by the equation $Fh=-kx$

• Fh = elastic restoring force (N)

• k = spring constant ($Nm^-1$) (the larger this number the stiffer the material)

• x = extension (m)

Stoke’s Law:

Viscous drag is defined as:

the frictional force between an object an a fluid which opposes the motion between the object and the fluid

It is calculated using Stoke’s Law: Fd=6πηrv

• Fd = viscous drag force (N)

• η = fluid viscosity ($Nsm^-2$ or Pa s)

• r = radius of the sphere (m)

• v = velocity of the sphere through the fluid ($ms^-1$)

The size of the force depends on the speed, size and shape of the object.

Archimedes principle:

Buoyancy is experience by a body partially or totally immersed in a fluid. The size of the force that produces this (known as upthrust) is equal to the weight of the water displacement.

It is equal to $Fb=pVg$

• Fb = buoyancy force (N)

• p = density of the fluid ($kgm^-3$)

• V = volume of the fluid displaced ($m³$)

• g = gravitational field strength ($ms^-2$)

Conservation of Linear Momentum:

The momentum of an object is defined as the product of mass and velocity. It is equal to $p=mv$.

• p = momentum ($kgms^-1$)

• m = mass (kg)

• v = velocity ($ms^-1$)

Momentum is a vector quantity, it has both magnitude and direction, and therefore can have both a negative or a positive value. The principle of conservation of liner momentum states that:

the total linear momentum before a collision is equal to the total linear momentum after a collision unless the system is acted on by a resultant external force

Impulse and Momentum:

Impulse is equal to the change or momentum of a system: J=Δp=mv-mu

• J = impulse (Ns)

• Δp = change in momentum ($kgms^-1$)

• m = mass (kg)

• v = final velocity ($ms^-1$)

• u = initial velocity ($ms^-1$)

It can also be defined in terms of the average resultant force: J=FΔt

• J = impulse (Ns)

• F = average resultant force (N)

• Δt = time of contact (s)

Force and Momentum:

The resultant force on a body is the rate of change or momentum, defined as: Δp=pf-pi

• Δp = change in momentum ($kgms^-1$)

• pf = final momentum ($kgms^-1$)

• pi = initial momentum ($kgms^-1$)

It can also be expressed as F= Δp/Δt

• F = resultant force (N)

• Δt = change in time (s)

Collisions and Explosions:

In both explosions and collisions momentum is always conserved. However, kinetic energy isn’t always. A collision (or explosion) is either elastic, if the kinetic energy is conserved, or inelastic, if it is not.

Angular Velocity:

The speed of an object going around in a circle remains constant, however its velocity changes. The speed of the object going around is equal to: 2πr/T

• r = radius of the circle (m)

• T = the time period (s)

Its frequency can be determined from the equation: f=1/T

• f = the frequency (Hz)

• T = the time period (s)

The angular speed of a body in circular motion (which is a scalar quantity) is defined as:

the rate of change in angular displacement with respect to time

We calculate it using the equation: ω= Δθ/Δt

• ω = angular speed ($rads^-1$)

• θ = angular displacement (rad)

• t = time taken (s)

The linear speed is related to the angular speed by the equation: v=rω

• v = linear speed ($ms^-1$)

• r = radius of circle (m)

• ω = angular speed ($rads^-1$)

Centripetal Force:

The centripetal force is defined as:

the resultant force perpendicular to the velocity required to keep a body in a uniform circular motion which acts towards the centre of the circle

It can be found using the equation: F=m$v²$/r

Or by the equation: F=mrω$²$

• F = centripetal force (N)

• v = linear speed ($ms^-1$)

• ω = angular speed ($rads^-1$)

• r = radius of the orbit (m)

• m = mass (kg)

Centripetal Acceleration:

Centripetal acceleration is defined as:

the acceleration of an object towards the centre of a circle when an object is in motion (rotating) around a circle at constant speed

It can be defined using the equation: a=v²/r

Or using the equation: a=ω²r

• a = centripetal acceleration ($ms^-2$)

• v = linear speed ($ms^-1$)

• r = radius of the circular orbit (m)

• ω = angular speed ($rads^-1$)

A3 - Work, Energy & Power

Principle of Conservation of Energy:

The principle of conservation of energy states that:

energy cannot be created or destroyed, it can only be transferred from one form to another

Therefore, the total amount of energy in a closed system (one without outside interference) must be constant.