AMT Final Day 1

Law of SInes

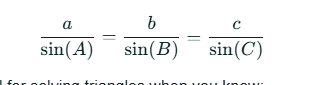
Law of Cosines

c² = a² + b² - 2ab cos(C).

Area of a Triangle (SAS, AAS)

AreaK=\frac12bc\sin a

Area of a Triangle (SSS)

AreaK=\sqrt{s(s-a)(s-b)(s-c)} s=\frac12\left(a+b+c\right)

magnitude

||v|| = √(a² + b²)

direction

tan\theta=\frac{v^2}{v^1} $$

Converting Polar to Rectangular

r²=x²+y²

x=r\cos\left(\theta\right)

y=r\sin(theta)

Quotient Identities

tan(\theta)=\frac{sin(\theta)}{cos(\theta)}

cot\left(\theta\right)=\frac{\cos\left(\theta\right)}{\sin\left(\theta\right)}

Pythagorean Identities

cos^{2}(\theta)+\sin^2\left(\theta\right)=1

1+tan^2\left(\theta\right)=\sec^2\left(\theta\right)

1+cot^2\left(\theta\right)=\csc^2\left(\theta\right)

Sum and Difference Equations (cos)

cos(a-b) =cosacosb+sinasinb

cos(a+b)=cosacosb-sinasinb

Sum and Difference Equations (sin, tan)

sin(a+b)=sinacosb+cosasinb

sin(a-b)=sinacosb-cosasinb

tan(a+b)=\frac{\tan a+\tan b}{1-\tan a\tan b}

tan\left(a-b\right)=\frac{\tan a-\tan b}{1+\tan a\tan b}