Exam 1 Study Guide
5.0(1)
Card Sorting
1/105
There's no tags or description
Looks like no tags are added yet.
Last updated 10:38 PM on 7/27/23
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
106 Terms
1
New cards
example of discipline use of logic
In Physics, often conclusions about how the world works is based on establishing a series of propositions with a line a reasoning to a conclusion and then trying to prove or disprove the propositions to determine if the conclusion is truth. An example would be the debate over whether light was a wave or a particle where experiments such as the photoelectric effect and Young's double slit experiment sought to prove one way or another until both were shown to be true and wave particle duality was understood.
2
New cards
example of logical reasoning in life
eating food stops hunger so if I am hungry, I should eat food.
3
New cards
good vs bad opinion
good vs bad basis and true/false premises
4
New cards
what is the inferential process involved in reasoning
The inferential process involved in reasoning uses premises based on truth to build on each other to show that something can lead to another thing and drawing conclusions from that path
5
New cards
main difference between good reasoning and bad reasoning
truth preservation
6
New cards
qualities of a model critical thinker
* Analytical Skills;
* Logical Reasoning;
* Open-Mindedness;
* Curiosity and Inquisitiveness;
* Intellectual Humility;
* Effective Communication;
* Problem-Solving Abilities;
* Information Literacy;
* Reflection and Awareness ;
* Ethical and Moral Integrity
* Logical Reasoning;
* Open-Mindedness;
* Curiosity and Inquisitiveness;
* Intellectual Humility;
* Effective Communication;
* Problem-Solving Abilities;
* Information Literacy;
* Reflection and Awareness ;
* Ethical and Moral Integrity
7
New cards
Peter’s saying
“The use of reason is a very passionate business”
Peter's saying about reason being a passionate business means that he thinks that in order to practice reason you have to be driven by a desire to know the truth, show empathy towards different perspectives, and drive towards accuracy. This passionate quest towards truth and accuracy drives the effort and internal thinking and analysis that is required to for good reason
Peter's saying about reason being a passionate business means that he thinks that in order to practice reason you have to be driven by a desire to know the truth, show empathy towards different perspectives, and drive towards accuracy. This passionate quest towards truth and accuracy drives the effort and internal thinking and analysis that is required to for good reason
8
New cards
Pierce’s saying
He says that preserving the truth and keeping an open mind and having other rational passion are crucial in developing a well constructed argument.
9
New cards
logic etymology
Logic comes from the Greek work logos for reason, calculation, or argument
10
New cards
reasoning activity
using the information presented to us in order to draw conclusions
11
New cards
why is logic a normative dicipline?
Logic is considered normative because if focuses on discussing and establishing norms for philosophy and thought.
It focuses less on how people do think and instead focuses on how they should think and reason. It talks about what are the correct ways of establishing an valid argument and drawing conclusions.
It focuses less on how people do think and instead focuses on how they should think and reason. It talks about what are the correct ways of establishing an valid argument and drawing conclusions.
12
New cards
motivations for Aristotle to form his logic (Aristotelian Logic/Categorical Syllogism)
systematic way of approaching arguments by describing categories and then determining the validity of an argument by the structure
13
New cards
Aristotle vs Socrates on education
Socrates advocated for education to push students towards reason in their thinking and passions and Aristotle advocated for rationality to be taught so education could develop people who were rational.
Both pushed for rationality but Socrates focused more on critical thinking and the specific thought processes around rational thought while Aristotle focused more on the idea of building people as a whole outside of just academics who behaved in rational manners intellectually and emotionally/morally.
Both pushed for rationality but Socrates focused more on critical thinking and the specific thought processes around rational thought while Aristotle focused more on the idea of building people as a whole outside of just academics who behaved in rational manners intellectually and emotionally/morally.
14
New cards
Siegle’s opinion on the fundamental aim of education
Siegel claims that the fundamental aim of education is the "**cultivation of reason**" where students are guided to be able to both:
* know how to reason
* be able to put together multiple propositions in support of or against a claim or their preexisting beliefs
* be guided by that reason
* listen to the results of rational lines of thinking, allow their opinions to change, and actually act on those conclusions or results instead of selectively ignoring them for convenience
* know how to reason
* be able to put together multiple propositions in support of or against a claim or their preexisting beliefs
* be guided by that reason
* listen to the results of rational lines of thinking, allow their opinions to change, and actually act on those conclusions or results instead of selectively ignoring them for convenience
15
New cards
4 reasons Siegel thinks fostering critical thinking in students is important
\
* __**respecting students as people**__ (this allows them the space to think for themselves and guide their own lives)
* __**preparing students for adulthood**__ (not pushing them into one role but allowing them to have self-direction and growth from that)
* supporting __**rational traditions**__ such as science, mathematics, and history (these fields rely on rational thinking and not mastering that prevents mastery or full understanding of the field)
* __**democratic life**__ (in order for democracy to work properly, citizens need to be able to employ careful analysis, good thinking, and deliberation otherwise they do not make informed and thought out decisions in their votes)
* __**respecting students as people**__ (this allows them the space to think for themselves and guide their own lives)
* __**preparing students for adulthood**__ (not pushing them into one role but allowing them to have self-direction and growth from that)
* supporting __**rational traditions**__ such as science, mathematics, and history (these fields rely on rational thinking and not mastering that prevents mastery or full understanding of the field)
* __**democratic life**__ (in order for democracy to work properly, citizens need to be able to employ careful analysis, good thinking, and deliberation otherwise they do not make informed and thought out decisions in their votes)
16
New cards
dispositions of the ideal critical thinker
* being clear on the intended meaning of what’s communicated
* determine and maintain focus on the conclusion or question
* take into account the total situation
* seek and offer reasons
* try to be well informed
* look for alternatives
* seek as much precision as the situation requires
* try to be reflexively aware of one’s own basic beliefs
* be open-minded of other points of view
* withhold judgement when evidence and reasons are insufficient
* take and change a position when the evidence and reasons are sufficient
* use one’s own critical thinking abilities
* determine and maintain focus on the conclusion or question
* take into account the total situation
* seek and offer reasons
* try to be well informed
* look for alternatives
* seek as much precision as the situation requires
* try to be reflexively aware of one’s own basic beliefs
* be open-minded of other points of view
* withhold judgement when evidence and reasons are insufficient
* take and change a position when the evidence and reasons are sufficient
* use one’s own critical thinking abilities
17
New cards
the 5 categories of abilities of a critical thinker
1. clarification
2. basis for decision
3. inference
4. metacognitive abilities
5. auxiliary critical thinking abilities
18
New cards
clarification abilities of a critical thinker
* identify the focus (issue, question, or conclusion)
* analyze the arguments
* ask or answer questions of clarification and/or challenge
* define terms, judge definitions, and deal with equivocation
* identify unstated assumptions
* analyze the arguments
* ask or answer questions of clarification and/or challenge
* define terms, judge definitions, and deal with equivocation
* identify unstated assumptions
19
New cards
basis abilities of a critical thinker
* judge the credibility of a source
* observe and judge observation reports
* observe and judge observation reports
20
New cards
inference abilities of a critical thinker
* deduce and judge deductions
* induce and judge inductions
* to generalizations
* to explanatory conclusions (yes hypothesis)
* make and judge value judgements
* induce and judge inductions
* to generalizations
* to explanatory conclusions (yes hypothesis)
* make and judge value judgements
21
New cards
metacognitive abilities of a critical thinker
* suppositional thinking
* integrate the other abilities and dispositions in making and defending a position
* integrate the other abilities and dispositions in making and defending a position
22
New cards
auxiliary abilities of a critical thinker
* proceed in an orderly manner appropriate to the situation
* follow problem solving steps
* monitor one’s own thinking
* employ a reasonable critical thinking checklist
* to be sensitive to the feelings, level of knowledge, and degree of sophistication of others
* employ appropriate rhetorical strategies in discussion and presentation
* employ and react to fallacy labels in an appropriate manner
* follow problem solving steps
* monitor one’s own thinking
* employ a reasonable critical thinking checklist
* to be sensitive to the feelings, level of knowledge, and degree of sophistication of others
* employ appropriate rhetorical strategies in discussion and presentation
* employ and react to fallacy labels in an appropriate manner
23
New cards
eternal statement
statement whose truth value never changes
24
New cards
eternal statement example
a dog is a mammal
25
New cards
occasion statement
statement whose truth value changes depending on the situation
26
New cards
occasion statement example
a dog is brown
27
New cards
invalid argument example
1. If I read a book I will learn
2. I like to read
3. so, I will learn
This argument is invalid because The conclusion, B is never connected to the second premise, C
28
New cards
valid argument with false conclusion example
1. If dogs are mammals, so are cats
2. dogs are not mammals
3. so, cats are not mammals
This is valid because it follows the modus tollens form so if the premises were true, so would the conclusion. The conclusion fails because of false premises
29
New cards
What is the structure of the following?
All presuppositions are statements that are taken to be true. Some statements that are taken to be true are false. So, no presuppositions are false.
All presuppositions are statements that are taken to be true. Some statements that are taken to be true are false. So, no presuppositions are false.
Premise 1. All A are B
Premise 2. Some B are C
Conclusion. So, no A are C
Premise 2. Some B are C
Conclusion. So, no A are C
30
New cards
What is the structure of the following?
Vice is not a weakness of character. For if a virtue is a desirable character trait, then a vice is a weakness of character. Either virtue is a desirable character trait or vice is a weakness of character. But virtue is not a desirable character trait
Vice is not a weakness of character. For if a virtue is a desirable character trait, then a vice is a weakness of character. Either virtue is a desirable character trait or vice is a weakness of character. But virtue is not a desirable character trait
Replacing terms:
1. not A
2. if B then A
3. Either C or A
4. but not B
rearranged into standard form:
1. Either C or A (prem 1)
2. if B then A (prem 2)
3. not B (prem 3)
4. so, not A (conclusion)
1. not A
2. if B then A
3. Either C or A
4. but not B
rearranged into standard form:
1. Either C or A (prem 1)
2. if B then A (prem 2)
3. not B (prem 3)
4. so, not A (conclusion)
31
New cards
types of invalid forms
1. affirming the adjunct
2. denying the antecedent
3. affirming the consequent
32
New cards
affirming the disjunct
1. Either A or B
2. A
3. So, not B
or
1. Either A or B
2. B
3. So, not A
33
New cards
denying the antecedent
1. If A then B
2. not A
3. not B
34
New cards
affirming the consequent
1. If A then B
2. B
3. So, A
35
New cards
inductive argument example
1. most orange cats are male
2. crookshanks is an orange cat
3. so, crookshanks is male
36
New cards
abductive argument example
1. it is September in Florida
2. there is no water or gas left anywhere
3. there is a hurricane coming
37
New cards
inductive vs deductive argument
inductive: premises imply a most likely conclusion
deductive: premises guarantee conclusion
deductive: premises guarantee conclusion
38
New cards
what is an argument?
a collection of statements with premises leading to a conclusion
39
New cards
what is a premise?
a sentence with a known truth value
40
New cards
types of deductive arguments (the do they work category)
valid and invalid
41
New cards
valid deductive argument
form that is truth preserving (mostly using the famous forms method)
42
New cards
sound argument
deductive argument with a valid form and all true premises
43
New cards
unsound argument
deductive argument with an invalid form and/or at leas one false premise
44
New cards
valid argument forms
1. modus ponens
2. modus tollens
3. hypothetical syllogism
4. constructive dilemma
5. disjunctive syllogism
6. form 6
7. form 7
45
New cards
modus ponens
1. If A then B
2. A
3. then B
46
New cards
modus tollens
1. If A then B
2. not B
3. then not A
47
New cards
hypothetical syllogism
1. if A then B
2. if B then C
3. so if A then C
48
New cards
constructive dillema
1. Either A or B
2. If A then C
3. If B then D
4. so either C or D
49
New cards
form 6
1. All A are B
2. C is A
3. C is B
50
New cards
Form 7
1. All A are B
2. C is not B
3. C is not A
51
New cards
How to test the validity of a deductive argument by the counterexample method
1. find structure by replacing term with symbols/letters
2. replace symbols with new terms with known and obvious truth values and try to get a false conclusion with all true premises while maintaining structure
52
New cards
good counterexamples use
statements with well known and eternal truth values
53
New cards
bad counterexamples use
broad, occasional, and/or ambiguous statements
54
New cards
categories for whether or not an inductive argument will work
strong and weak
55
New cards
strong inductive arguments are
most likely to be true
56
New cards
weak inductive arguments are
unlikely to be true
57
New cards
cogent arguments
strong inductive arguments with all true premises
58
New cards
uncogent arguments
inductive arguments that are weak and/or have at least one false premise
59
New cards
types of inductive arguments
1. __**statistical syllogism**__ (percentages)
2. __**argument by authority**__ (an expert in the field said this so it’s probably true)
3. __**argument by analogy**__ (must have a relevant connection)
4. __**abductive argument**__ (open ended premises)
60
New cards
standard forms of categorical propositions (A E I O)
A All S are P
E No S are P
I Some S are P
O Some S are not P
E No S are P
I Some S are P
O Some S are not P
61
New cards
how to determine relationships between categorical propositions
Aristotelian Square
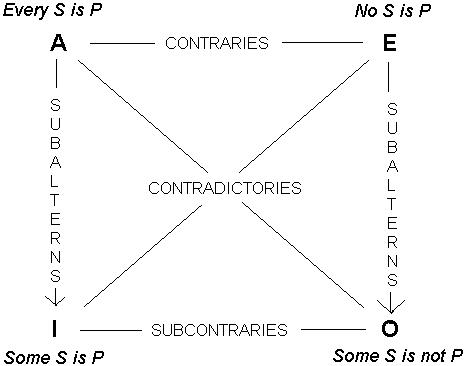
62
New cards
Stylistic variants of A (all S are P)
* every S is a P
* each S is a P
* any S is a P
* if anything is an S, then it is a P
* things are S only if they are P
* only S are P
* each S is a P
* any S is a P
* if anything is an S, then it is a P
* things are S only if they are P
* only S are P
63
New cards
Stylistic variants of E (no S are P)
* nothing that is an S is a P
* a thing is an S only if it is not a P
* if any thing is an S then it is not a P
* Nothing is an S unless it is not a P
* a thing is an S only if it is not a P
* if any thing is an S then it is not a P
* Nothing is an S unless it is not a P
64
New cards
Stylistic variants of I (Some S are P)
* there are S that are P
* at least one S is a P
* there exists an S that is a P
* something is both an S and a P
* at least one S is a P
* there exists an S that is a P
* something is both an S and a P
65
New cards
Stylistic variants of O (Some S are not P)
* at least one S is not a P
* not all S are P
* not every S is a P
* something is an S but not a P
* there is an S that is not a P
* not all S are P
* not every S is a P
* something is an S but not a P
* there is an S that is not a P
66
New cards
argument form
is a pattern of reasoning
67
New cards
substitution instance
an argument that results from uniformly replacing the variables in that form with statements (or terms)
68
New cards
valid argument form
one in which every substitution instance is a valid argument
69
New cards
formally valid argument
one that is valid in virtue of its form.
70
New cards
negation
of a statement is its denial
71
New cards
conditional statement
is an if-then statement, often simply called a “conditional.”
72
New cards
antecedent
The if-clause of a conditional
73
New cards
consequent
The then-clause of a conditional
74
New cards
disjunction
is an either-or statement
75
New cards
disjuncts
The statements comprising a disjunction
76
New cards
fallacy of denying the antecedent
is an invalid argument form: If A, then B; not A; so, not B
77
New cards
n invalid argument form
one that has some invalid substitution instances.
78
New cards
counterexample
a substitution instance in which the premises are true and the conclusion is false
79
New cards
good counterexample
a substitution instance in which the premises are well-known truths and the conclusion is a well-known falsehood.
80
New cards
fallacy of affirming the consequent
an invalid argument form: If A, then B; B; so, A.
81
New cards
categorical statement
a statement that relates two classes or categories, where a class is a set or collection of things
82
New cards
term
a word or phrase that stands for a class of things
83
New cards
strong argument
one in which it is probable (but not necessary) that, if the premises are true, then the conclusion is true
84
New cards
weak argument
one in which it is not probable that, if the premises are true, then the conclusion is true
85
New cards
cogent argument
a strong argument in which all of the premises are true.
86
New cards
uncogent argument
one that is either weak or strong with at least one false premise
87
New cards
Deductive logic
the part of logic that is concerned with the study of methods of evaluating arguments for validity and invalidity.
88
New cards
Inductive logic
the part of logic that is concerned with the study of methods of evaluating arguments for strength and weakness
89
New cards
categorical statement
a statement that relates two classes or categories.
90
New cards
subject term
the first noun or noun phrase that appears in a categorical statement when it is put into standard form
91
New cards
predicate term
the second noun or noun phrase that appears in a categorical statement when it is put into standard form
92
New cards
affirmative statement
some or all of the members of the class denoted by the subject term are also members of the class denoted by the predicate term
93
New cards
negative statement
denies that some or all of the members of the class denoted by the subject term are also members of the class denoted by the predicate term
94
New cards
universal statement
makes a claim about everything in the class denoted by its subject term
95
New cards
particular statement
only makes a claim about something in the class denoted by its subject term
96
New cards
stylistic variant
a different way of saying the same thing
97
New cards
Corresponding statements
categorical statements having the same subject term and the same predicate term
98
New cards
contradictories
Two statements that cannot both be true and they cannot both be false
99
New cards
contraries
Two statements are contraries that cannot both be true but they can both be false
100
New cards
necessary truth
a statement that cannot be false under any possible circumstances