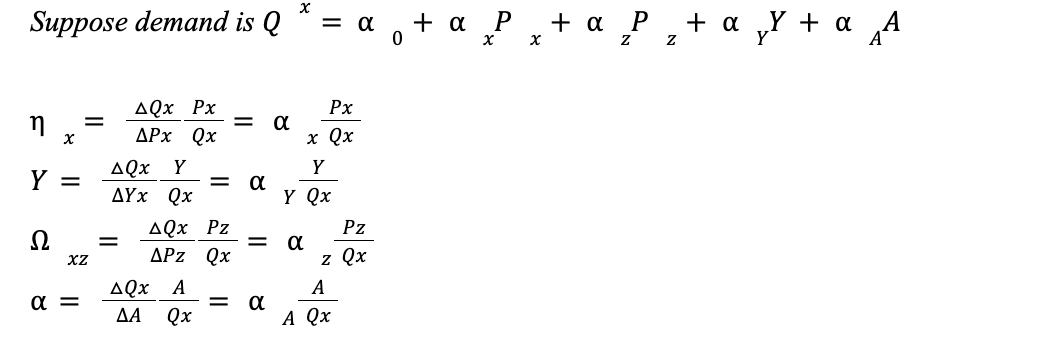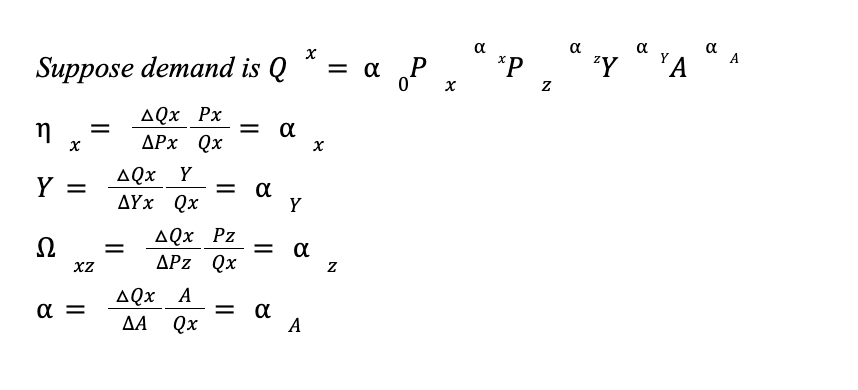AEM 2600 Prelim 1 Formulas

Economic profits 

= TR-TC

Present Value: 

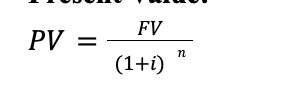
Stream of Future payments

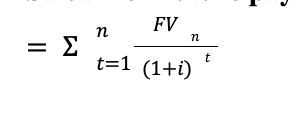
Net Present Value

NPV=PV-Current Costs

Marginal Profits (pi)

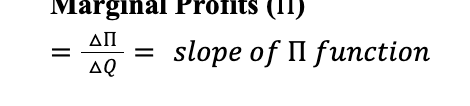
Average Profits ()

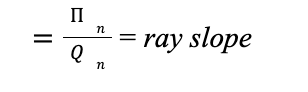
Rules of Derivation: power rule 

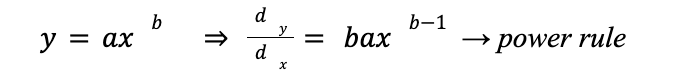
Rules of Derivation: product rule

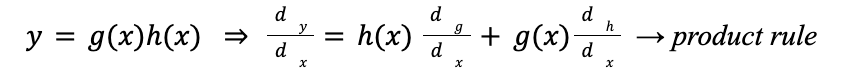
Rules of derivation

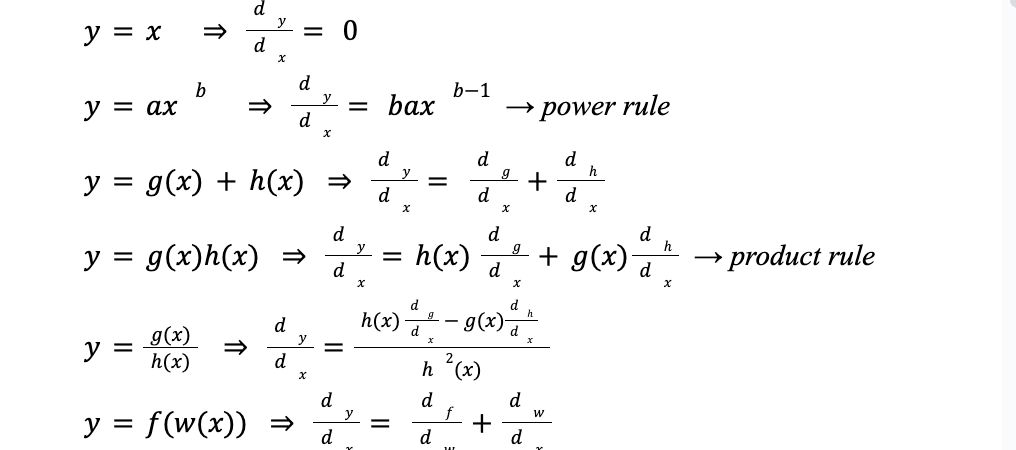
 when the first derivative of a function = 0 that function is at a max/min (optimum) 

→ if second derivative is (-): max

→ if second derivative is (+): min

Constrained Optimization 

1. Restrate the constraint so equal to 0

2. Restate the objective function as a Lagrangian with constraints added in, premultiplied by Lagrangian

   1. Ex.

      

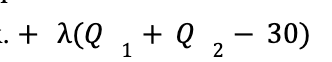
3. Take partial derivatives with respect to all variables and lagrangian multiplier, set =0 and solve

Demand

→ Where P_x is own price, P_z is price of related goods, Y is income, Pop is population (size of market and composition), A is advertising, t is taste, is expectations 

Supply

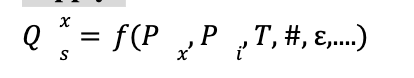
→ Where P_x is own price, P_i is price of inputs, T is technology, # is number of firms in the market, is expectations 

Slope for the descartes cartesian plane

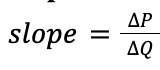
Taxes revenues and expenditures

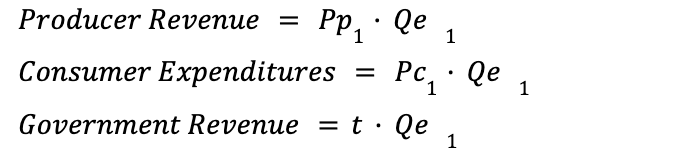
Taxes types

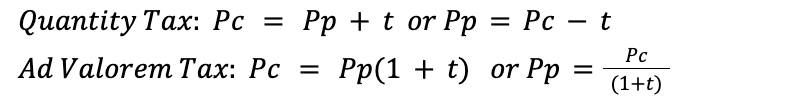
Subsidy revenues and expenditures

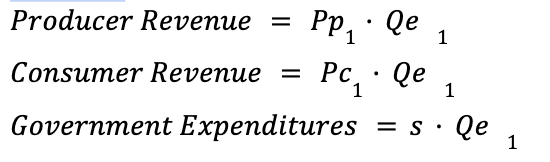
Subsidy types

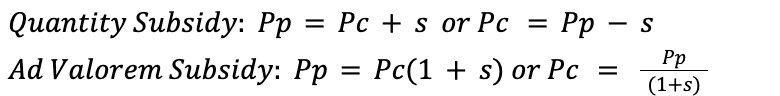
Burden and Benefit

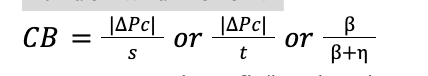
→ consumer benefit/burden depends on the elasticity of supply relative to the sum of the two elasticities

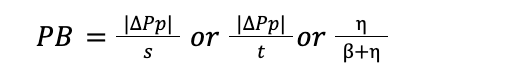
→ producer benefit/burden depends on elasticity of demand relative to the sum of two elasticities

Own Price Elasticity of Demand

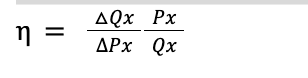
Total Revenue

F(Q) = PQ

where P is inverse demand

Marginal Revenue

Optimal Price of a good (MR=MC)

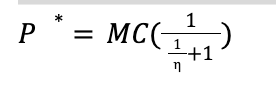
Income Elasticity of Demand

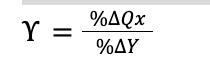
Cross Price Elasticity of Demand

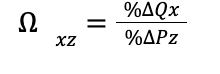
Advertising Elasticity of Demand

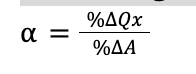
Elasticity of Supply

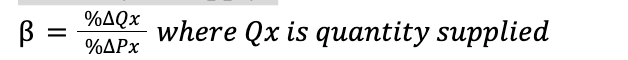
Obtaining Elasticities from Demand Functions