vectors(y1)

vectors

represent a movement with magnitude and direction

drawn using directed line segments

representing vectors

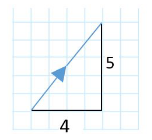
vectors can be drawn on a graph, this is useful for representing the displacement change relative to the x and y axes

they can be written by containing the x and y displacement co-ordinates in brackets with the x value above the y, known as a column vector

vector addition and subtraction

visually:

one vector is attached to another, the resulting vector can be determined by drawing a line from the start of the first vector to the end of the other, forming a triangle

to subtract a vector the vector's direction is reversed before it is added

numerically:

the individual axis values of each vector are added or subtracted

vector multiplication

multiplying a vector by a scalar is done by multiplying the length(or the co-ordinate change from one end to another) by said scalar

multiplying by negative numbers reverses the direction

unit vectors

vectors with a magnitude of 1

they may have an x co-ordinate change of 1 and a y co-ordinate change of 0 (i) or vice versa (j)

any two-dimensional vectors can be written as pi+qj

they may also be diagonal(x and y co-ords between 0 and 1)

calculating a unit vector

a unit vector in the direction of a is a/|a|

(where a is the vector and |a| is the scalar magnitude)

vector magnitude and direction

the magnitude of a vector is calculated using pythagoras

direction is calculated using trigonometry, expressed as an angle anticlockwise from the positive x axis(unless otherwise specified)

parallel vectors

two vectors are parallel if they are scalar multiples of eachother

position vectors

vectors describing the position of a point in relation to the origin

notated as OP with an arrow pointing right on top, where O is the origin and P is the point