AQA A LVL Physics - Waves

2 main types of wave

Transverse and Longitudinal

Progressive waves transfer ______, not ______

Energy, matter

Waves are produced by...

particles (of a medium) or fields oscillating at the source

Evidence showing that waves carry energy:

Heating, physical vibration, loss of energy from the source, electricity generation, ionisation

Longitudinal waves - the direction of particle/field oscillations is ________ to the direction of energy propagation.

Parallel

Longitudinal waves contain ____________ and ____________

compressions, rarefactions

what are longitudinal waves made up of

compressions

rarefactions

on a regular wave that represents a longitudinal wave, where are the compressions, and where are the rarefactions

peaks = compressions

troughs = rarefactions

Transverse waves - the direction of particle/field oscillations is _____________ to the direction of energy propagation.

Perpendicular

Wavelength symbol

definition

what is its units

• lamda

• the length of one whole oscillation (e.g the distance between successive peaks or troughs)

• measured in m

Displacement

Distance and direction from equilibrium (rest) position

Amplitude symbol

definition

what is it measured in?

• A

• Maximum displacement from equilibrium position

• measured in m

Time period symbol

definition

what is it measured in

• T

• Time taken for one full oscillation

• units are s

frequency symbol

definition

what are its units

what is the SI base unit of this unit

• f

• the number of complete oscillations passing through a point per second

• measured in Hz (hertz)

• SI of Hz = s^-1

speed symbol

definition

what are its units

• c

• distance travelled by the wave per unit time

• ms^-1

What is intensity proportional to

the amplitude squared

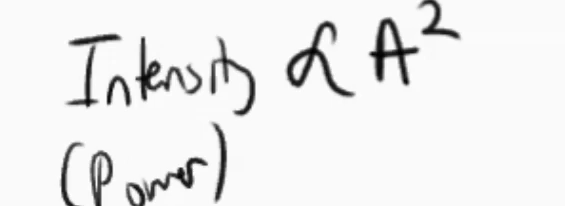
give some examples of what I mean by applications of intensity

e.g hint intensity, light intensity….

(In terms of time and displacement) V =

s/t

T =

1/f

(In terms of waves) V =

f x λ

c =

f x λ

Examples of longitudinal waves

Sound waves, P waves

Examples of transverse waves

S waves, EM waves, water, waves on string

Examples of both transverse and longitudinal waves

Mechanical waves, L waves

Sound wave properties

Longitudinal, produced by the vibration of particles in a medium

What waves do polaroid sunglasses involve?

EM waves

EM wave properties

transverse, have oscillating electric and magnetic fields at right-angles to eachother and the direction of propagation

A wave is unpolarised when...

transverse oscillate in more than 1 plane

how do polaroid sunglasses reduce glare?

• they block partially polarised light, (e.g thats reflected from water or tarmac)

• they only allow oscillations in the plane of the filter, making it easier to see

Can transverse waves be polarised?

Yes

How can transverse waves be polarised?

by using a polarising filter, which only lets oscillations in one plane through

Can longitudinal waves be polarised?

no

Why can't longitudinal waves be polarised?

Only have 1 plane of oscillations (they oscillate in the same direction as they travel)

can longitudinal waves travel in a vacuum?

no

How are TV signals polarised?

By the orientation of the rods on the transmitting aerial (which have to be aligned)

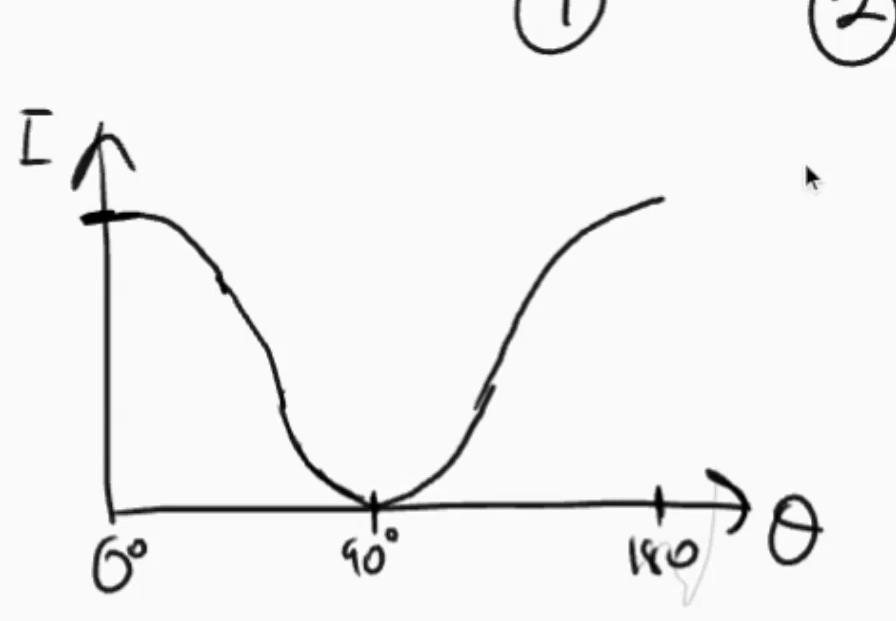
on the graph of Intensity against theta (for polarisation / rotation of a polarising filter), what graph is it?

a cos² graph (a cos graph but where -1 is the x axis)

wave front

leading edge of a moving wave 

rays

lines drawn through the wavefronts at 90 degrees

phase definition

what units does it have

• A measure of how far through a wave’s cycle a given point on the wave is

• units are radians, degrees, or fractions of a cycle

phase difference definition

what units is it measured in

• how much a particle / wave lags behind another particle / wave. 

what 2 things are needed for 2 points on a wave to be in phase?

• if they are the same point of the wave cycle

• need the same frequency and wavelength

how can u find the phase difference using the wavelength (eqtn)

phase diff =

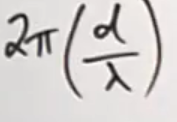
how can u find the phase difference using the Time period (eqtn)

phase diff = 

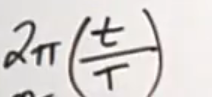
path difference

A measure of how far ahead a wave is compared to another wave. (the difference in distance travelled by 2 waves)

• usually expressed in terms of wavelength

90 degrees phase difference in radians

0.5π

180 degrees phase difference in radians

π

monochromatic definition

1 wavelength/frequency

coherent (light source) definition

same frequency and wavelength, and a fixed/constant phase difference

give an example of a source of light which is coherent and monochromatic

a laser

superposition

when waves meet, pass through eachother and combine

principle of superposition

when 2 waves meet, the total displacemenet at a point is equal to the total sum of the individual displacemenets at that point

constructive interference

when waves reinforce, creating supercrests and supertroughs

destructive interference

when waves cancel eachother out

constructive interference occurs when:

waves meet in phase, phase difference = 0 or 360, path difference = n*wavelength

destructive interference happens when:

waves meet in anti phase, phase difference = 180, path difference = (n+0.5)*wavelengths

interference examples

sound waves using 2 loudspeakers, wavter waves in a ripple tank, mircrowave with chocolate buttons

stable interference patterns form when...

the wave sources are coherent

stationary (standing) wave

superpostion of 2 coherent progressive waves moving in opposite directions

when is a stationary wave formed

its formed from the superposition of 2 progressive waves travelling in opposite directions, with the same freq, wavelength and amplitude

what are the necessary conditions for a stationary wave to happen

• the progressive waves need to be travelling in opposite directions

• the progressive waves must have the same frequency, amplitude, wavelength

what 3 things need to be the same for the progressive waves that make a standing wave 

• frequency

• amplitude

• wavelength

nodes definition

points of 0 amplitude/displacement in a stationary wave

antinodes definition

points of maximum amplitude/displacement in a stationary wave

Standing waves have:

nodes, antinodes, no energy transferred

Standing waves have the ability to..

be formed in sound waves (in tubes), microwaves and on a string (using a driving oscillator)

where will constructive interference occur on a standing wave?

where will destructive interference occur on a standing wave?

constructing interference = antinode

destructive interference = node

the number of_____________represents which harmonic it is

anitnodes

First harmonic (fundamental frequency) length

½ Wavelength

2nd harmonic Length

Wavelength

3rd harmonic Length

3/2 Wavelength

To calculate the frequency of harmonics:

Recicopral of wavelenth fraction fitted in to V/L (eg. λ of 2/3L would be 3V/2L, which = 3f0)

how can u calculate the frequency of second and third harmonics based on the frequency of 1st harmonic

Frequency (of first harmonic) x 2 = freq of 2nd harmonic

Frequency (of first harmonic) x 3 = freq of 3rd harmonic

this continues for n^th harmonic

mathematical equation that links wavelength, length (e.g of string) and n^th harmonic

L = n/2 wavelength

how are stationary microwaves formed?

how can nodes and antinodes of a stationary microwave be found

• formed by reflecting a microwave beam at a metal plate.

• nodes and antinodes can be found using a microwave probe

how can a stationary sound wave be formed?

what happens to the antinodes and nodes

place a speaker at 1 end of a glass tube

put powder at bottom of tube

antinodes will be shaken, and nodes will be settled

Mathmatical equation linking speed, tension and mass per unit length

v = square root(tension/mass per unit length)

how do you calculate mass per unit length, µ =

Mass (kg) / Length (m)

how do you calculate Tension (T) if the harmonic is done by a string attached to masses over a pulley

m*g

for any wave: f =

(n/2L) * square root(T/mass per unit length)

what is the first harmonic equation to find frequency, and what does every term mean

L = length of the vibrating string

T = tension

μ = mass per unit length

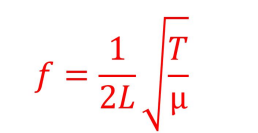
in a tube, when talking about harmonics, what is formed at an open end?

an antinode

in a tube, when talking about harmonics, what is formed at a closed end?

a node

When does maximum diffraction occur?

when gap = wavelength

(roughly)

when does minor/unnoticeable diffraction occur?

when gap > wavelength

when are waves mostly reflected back?

when gap < wavelength

what happens when a wave meets an object/obstacle

you get diffraction around the edges

what happens to the diffraction when the obstacle gets wider, compared to the wavelength

less diffraction happens

what 4 safety precautions must you do when dealing with lasers

• wear laser safety goggles

• dont shine the laser at reflective surfaces

• display a warning sign

• never shine the laser at a person

when doing a double slit experiment, how can u get a coherent and monochromatic light, without depending on a monochromatic and coherent light source.

• use a single slit to make it have a fixed path difference,

• and use a filter to make the light monochromatic

• then send it through the double slit

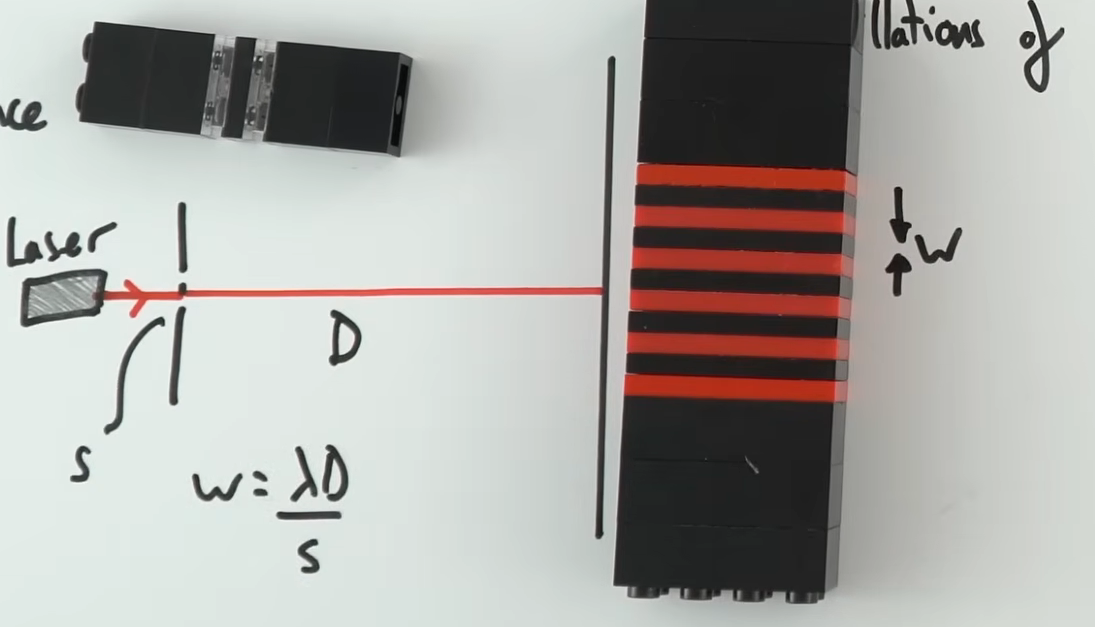
what is young’s double slit fringe spacing equation, and what does each term represent?

w = fringe width / spacing

s = slit separation

D = distance from slit to screen

λ = wavelength

using white light (for YDS) instead of monochromatic laser light gives _________maxima and a _________ intense diffraction pattern

wider, less

if we use white light with for any diffraction experiment, what will the diffraction pattern look like

a central white fringe, with alternating bright fringes (which are spectra), violet is closest to central maxima, and red furthest

when using white light for any diffraction experiment, what colour is closes to white central max, and which is furthest

closest = violet light

furthest = red light

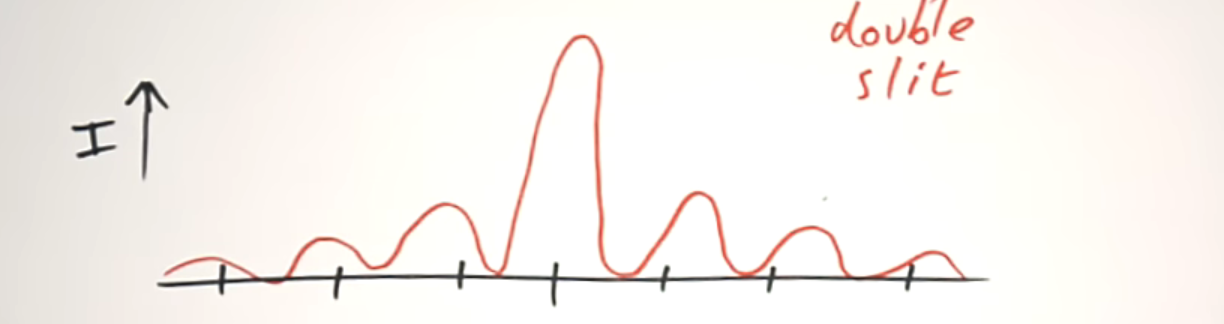
what does the double slit intensity graph look like?

what are the 2 accepted ways of drawing this graph?

• the intensity of the fringes gradually decrease from the central maxima on both sides

OR

• the intensity of the fringes stay the same as the central maxima

(experiment 1) Monochromatic light through one slit: type of interference

destructive at minima

constructive at maxima

for single slit diffraction, what does the diffraction pattern look like for monochromatic light?

describe it

• has a bright central fringe which is double the width of all other fringes

• alternating bright and dark fringes on either side of central maxima

(experiment 2) White light through 1 slit: observations

central fringe white, then others 'rainbow fringes', different colours in white light diffracted by different amounts, dark fringes still present between rainbow fringes.

larger wavelength further away from white central maxima

what does the graph of intensity of maximas look like for a single slit?

describe 2 key features of it

• the central maxima is very bright compared to the rest of the fringes

• the width of the central maxima is double the width of the other fringes

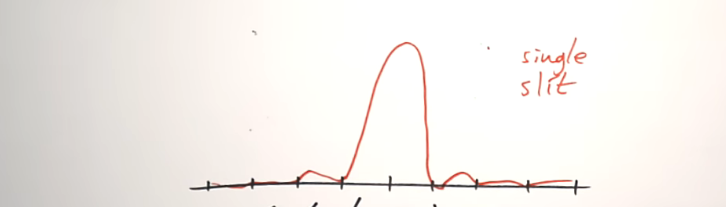
for both single and double slit intensity graphs, what has to happen for it to be drawn correctly

must touch the “x axis” —> shows dark fringe

what should the diffraction grating/slit size roughly be equal to

the laser light wavelength