Maths: Representing Data (GCSE, Edexcel)

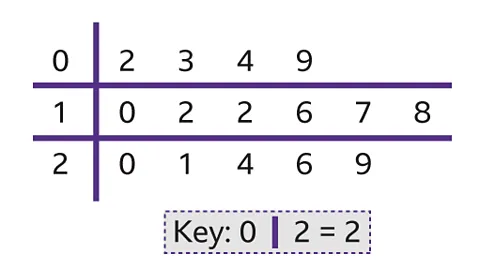
Stem and Leaf Diagram

A glorified table with 2 columns that sorts data by their most significant place value:

• The 1st column, “the stem”, is the column that defines the most significant place value. It is one number per row only.

• The 2nd column, “the leaves”, is the column that the data is placed into. Data is placed without the stem place value and multiple numbers can occupy a row.

A key is required to show the conversion between stem/leaf and data point.

Averages from a Stem and Leaf Diagram

The process remains the exact same as if it were a set, except now the values must be extrapolated.

Pie Chart and Angle rule

The fraction of the angle over 360 is equivalent to the fraction of people.

Cumulative Frequency Diagram

A curved line graph generated with a cumulative frequency (running total) table.

Cum Freq Coordinate generation strategy

• If there is no column for cumulative frequency, make one and keep a running total of the frequencies.

• The x-coordinate is the upper bound of the class interval, whereas the y-interval is the corresponding cumulative frequency.

• Do this for each row.

Median from a Cum Freq Diagram

• Find the place of the median by doing n/2 (this is a diagram).

• Treat the place as a y-value and find its corresponding x-value.

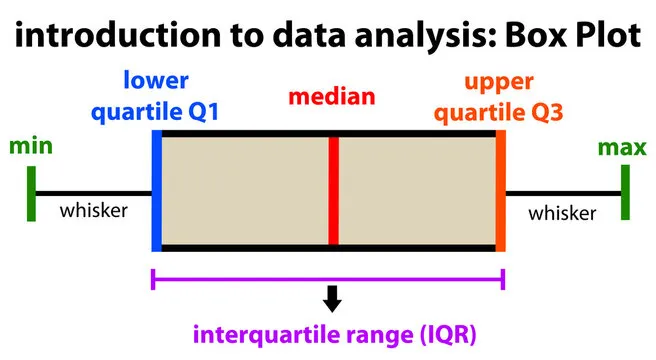
Inter-Quartile Range

A measurement of the data spread aimed at reducing the impact of extreme values, by only considering the middle 50% of values.

IQR formula

upper quartile - lower quartile

IQR from a Cum Freq Diagram

• Find the places for the 2 quartiles by doing n/4 (lower quartile) and 3n/4 (upper quartile).

• Treat the places like y-values and find their corresponding x-values to find the values of the quartiles.

• Find the IQR using the formula.

Box Plot

A diagram used to compare sets of data. It represents the smallest value, lower quartile, median, upper quartile and largest value.

Finding quartiles in a set

Split the list into 2 lists of equal size. Discard the median if the total number of numbers in the set is odd. Find the median of both smaller lists to find the 2 quartiles.

Comparing Box Plots

Compare the median and the IQR. You must explain what it means, so for median it is “x was better/worse on average“ and for IQR it is “x was less/more consistent“.

IQR consistency

A higher IQR means less consistency in results, whereas a lower IQR indicates more consistency in results.

Histograms

A way to display grouped data frequencies similarly to a bar chart. Normally the class interval widths are unequal.

Frequency Density

The y-axis for a histogram, NOT frequency. DO NOT plot against frequency when drawing a histogram.

Frequency Density formula

For each data point:

frequency / class width

Frequency graphics in a histogram

The area of the bar represents the frequency.

“A number of data points are more/less than x, Find x” (HISTOGRAMS)

• If the question states more start from the right, if it sates less than start from the left.

• Move towards the middle, keeping track of the total frequency by calculating the area. This may include splitting up bars.

• The x-axis value for when you reach the desired number is the number.

Median and IQR from a histogram strategy

• Find the frequency total if it is not given to you

• Start from the left

• Move towards the middle, keeping track of the total frequency by calculating the area. This may include splitting up bars.

• When you reach your desired value (n/2 for median; n/4 for lower quartile; and 3n/4 for upper quartile) the x-axis is the median/quartile.

“There are a number of data points in a range that spans multiple bars, find the frequency of a different range. There is no scale” (HISTOGRAMS)

• Find the area of the given range in squares (it’s graph paper).

• Find how much 1 square is worth in terms of real frequency.

• Find the area of the wanted range in squares.

• Convert to real frequency.

Frequency Polygon

A type of line graph, that shows the values of a frequency table.

Frequency polygon coordinate generation

• Find the midpoint for each class interval.

• The x-value is the midpoint and the y-value is the frequency.

• Repeat for each row to find all the coordinates.

Generating a frequency table from a polygon

• Find the values the midpoints are between on the x-axis. This will basically be choreographed to you.

• Now you have all the values you need (frequency and class interval) to created the grouped frequency table.

You can then use that to find any average.