Ch 19 - Linear Programming

Linear programming techniques will always produce an optimal solution to an LP problem. (T/F 1)

False 1

LP problems must have a single goal or objective specified. (T/F 1)

True 1

Constraints limit the alternatives available to a decision maker. (T/F 2)

True 2

Profit maximization could be an objective of an LP problem; but cost minimization cannot be the objective of an LP problem. (T/F 2)

False 2

The feasible solution space only contains points that satisfy all constraints. (T/F 3)

True 3

The equation 5x + 7y = 10 is linear. (T/F 4)

True 4

The equation 3xy = 9 is linear. (T/F 3)

False 3

Graphical linear programming can handle problems that involve any number of decision variables. (T/F 4)

False 4

An objective function represents a family of parallel lines. (T/F 5)

True 5

The term isoprofit line means that all points on the line will yield the same profit. (T/F 6)

True 6

The feasible solution space is the set of all feasible combinations of decision variables as defined by only binding constraints. (T/F 5)

False 5

The value of an objective function always decreases as it is moved away from the origin. (T/F 6)

False 6

A linear programming problem can have multiple optimal solutions. (T/F 7)

True 7

A maximization problem is limited by all greater than or equal to constraints. (T/F 7)

False 7

If a single optimal solution exists to a graphical LP problem, it will exist at a corner point. (T/F 8)

True 8

The simplex method is a general-purpose LP algorithm that can be used for solving only problems with more than six variables. (T/F 8)

False 8

A change in the value of an objective function coefficient does not change the optimal solution. (T/F 9)

False 9

The term range of feasibility refers to a constraint's right-hand-side quantity. (T/F 9)

True 9

A shadow price indicates how much a one-unit decrease/increase in the right-hand-side value of a constraint will decrease/increase the optimal value of the objective function. (T/F 10)

True 10

The term range of feasibility refers to coefficients of the objective function. (T/F 10)

False 10

Nonzero slack or surplus is associated with a binding constraint. (T/F 11)

False 11

In the range of feasibility, the value of the shadow price remains constant. (T/F 11)

True 11

Every change in the value of an objective function coefficient will lead to changes in the optimal solution. (T/F 12)

False 12

Nonbinding constraints are not associated with the feasible solution space; i.e., they are redundant and can be eliminated from the matrix. (T/F 13)

False 13

When a change in the value of an objective function coefficient remains within the range of optimality, the optimal solution also remains the same. (T/F 12)

True 12

Using the enumeration approach, optimality is obtained by evaluating every coordinate. (T/F 14)

False 14

The linear optimization technique for allocating constrained resources among different products is:

Linear Programming

Which of the following is not a component of the structure of a linear programming model?

Environmental Uncertainty

Coordinates of all corner points are substituted into the objective function when we use the approach called:

Enumeration

Which of the following could not be a linear programming problem constraint?

1A + 2B

For the products A, B, C, and D, which of the following could be a linear programming objective function?

Z = 1A + 2B + 3C + 4D

The logical approach, from beginning to end, for assembling a linear programming model begins with:

Identifying the decision variables

The region which satisfies all of the constraints in graphical linear programming is called the:

Feasible solution space

In graphical linear programming to maximize profit, the objective function is:

        I.    A family of parallel lines

      II.    A family of isoprofit lines

    III.    Interpolated

IV. Linear

I, II, and IV only

Which objective function has the same slope as this one: $4x + $2y = $20?

$4x + $2y = $10

In graphical linear programming, when the objective function is parallel to one of the binding constraints, then:

Multiple optimal solutions exist

The theoretical limit on the number of decision variables that can be handled by the simplex method in a single problem is:

Unlimited

A shadow price reflects which of the following in a maximization problem?

Marginal gain in the objective that would be realized by adding one unit of a resource

In linear programming, a nonzero reduced cost is associated with a:

Decision variable not in the solution

A constraint that does not form a unique boundary of the feasible solution space is a:

Redundant Constraint

In linear programming, sensitivity analysis is associated with:

        I.     A family of parallel lines

      II.     A family of isoprofit lines

III. Interpolated

I, II, and III

In a linear programming problem, the objective function was specified as follows:

 

Z = 2A + 4B + 3C

 

The optimal solution calls for A to equal 4, B to equal 6, and C to equal 3. It has also been determined that the coefficient associated with A can range from 1.75 to 2.25 without the optimal solution changing. This range is called A's:

Range of Optimality

An analyst, having solved a linear programming problem, determined that he had 10 more units of resource Q than previously believed. Upon modifying his program, he observed that the list of basic variables did not change, but the value of the objective function increased by $30. This means that resource Q's shadow price was:

$3.00 | 30/10 = 3

In the graphical approach to linear programming, finding values for the decision variables at the intersection of corners requires the solving of:

Simultaneous Equations

A redundant constraint is one that:

Does not form a unique boundary of the feasible solution space.

The production planner for Fine Coffees, Inc., produces two coffee blends: American (A) and British (B). Two of his resources are constrained: Columbia beans, of which he can get at most 300 pounds (4,800 ounces) per week; and Dominican beans, of which he can get at most 200 pounds (3,200 ounces) per week. Each pound of American blend coffee requires 12 ounces of Colombian beans and 4 ounces of Dominican beans, while a pound of British blend coffee uses 8 ounces of each type of bean. Profits for the American blend are $2.00 per pound, and profits for the British blend are $1.00 per pound.

 

What is the objective function?

$2A + $1B = Z

The production planner for Fine Coffees, Inc., produces two coffee blends: American (A) and British (B). Two of his resources are constrained: Columbia beans, of which he can get at most 300 pounds (4,800 ounces) per week; and Dominican beans, of which he can get at most 200 pounds (3,200 ounces) per week. Each pound of American blend coffee requires 12 ounces of Colombian beans and 4 ounces of Dominican beans, while a pound of British blend coffee uses 8 ounces of each type of bean. Profits for the American blend are $2.00 per pound, and profits for the British blend are $1.00 per pound. 

 

What is the Columbia bean constraint?

12A + 8B ≤ 4,800

The production planner for Fine Coffees, Inc., produces two coffee blends: American (A) and British (B). Two of his resources are constrained: Columbia beans, of which he can get at most 300 pounds (4,800 ounces) per week; and Dominican beans, of which he can get at most 200 pounds (3,200 ounces) per week. Each pound of American blend coffee requires 12 ounces of Colombian beans and 4 ounces of Dominican beans, while a pound of British blend coffee uses 8 ounces of each type of bean. Profits for the American blend are $2.00 per pound, and profits for the British blend are $1.00 per pound. 

 

What is the Dominican bean constraint?

4A + 8B ≤ 3,200

The production planner for Fine Coffees, Inc., produces two coffee blends: American (A) and British (B). Two of his resources are constrained: Columbia beans, of which he can get at most 300 pounds (4,800 ounces) per week; and Dominican beans, of which he can get at most 200 pounds (3,200 ounces) per week. Each pound of American blend coffee requires 12 ounces of Colombian beans and 4 ounces of Dominican beans, while a pound of British blend coffee uses 8 ounces of each type of bean. Profits for the American blend are $2.00 per pound, and profits for the British blend are $1.00 per pound. 

 

Which of the following is not a feasible production combination?

400 A and 0B

The production planner for Fine Coffees, Inc., produces two coffee blends: American (A) and British (B). Two of his resources are constrained: Columbia beans, of which he can get at most 300 pounds (4,800 ounces) per week; and Dominican beans, of which he can get at most 200 pounds (3,200 ounces) per week. Each pound of American blend coffee requires 12 ounces of Colombian beans and 4 ounces of Dominican beans, while a pound of British blend coffee uses 8 ounces of each type of bean. Profits for the American blend are $2.00 per pound, and profits for the British blend are $1.00 per pound. 

 

For the production combination of 0 American and 400 British, which resource is "slack" (not fully used)?

Colombian beans (only) | 4800 > 3200

A novice linear programmer is dealing with a three-decision-variable problem. To compare the attractiveness of various feasible decision-variable combinations, values of the objective function at corners are calculated. This is an example of:

Enumeration

When we use less of a resource than was available, in linear programming that resource would be called non-________.

Binding

Once we go beyond two decision variables, typically the ________ method of linear programming must be used.

Simplex

________ is a means of assessing the impact of changing parameters in a linear programming model.

Sensitivity Analysis

For a linear programming problem with the following constraints, which point is in the feasible solution space assuming this is a maximization problem?

x = 2, y = 1

Which of the following choices constitutes a simultaneous solution to these equations?

x = 2, y = 1

What combination of x and y will provide a maximum for this problem?

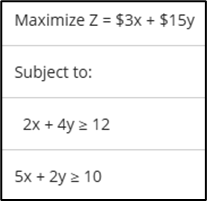
x = 0, y = 5