CSCE 222 Flash Cards

Conjunction Distributing Over Disjunction

Disjunction Distributing Over Conjunction

Sort of like the distributive, no signs are flipped.

(Disjunction Distributing Over Conjunction same idea)

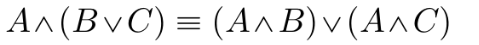
Associative Law

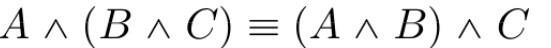
Communicative Law

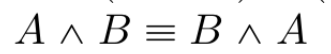
idempotence law

*three equal signs: always equal, identity meaning

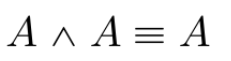
identity law

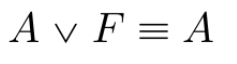
domination law

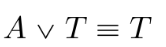
De Morgan’s Law

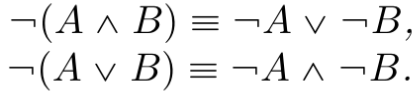
Absorption law for conjunction and for disjunction

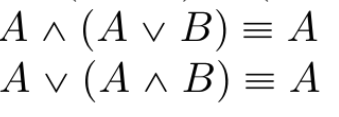
Double negation law

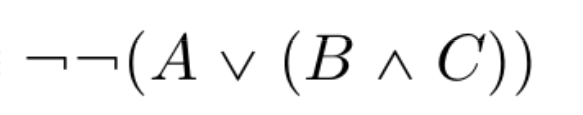
vacuously true

Modeus Ponus Proof

Implication law

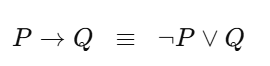
Sets

has elements in them, elements can be infinite

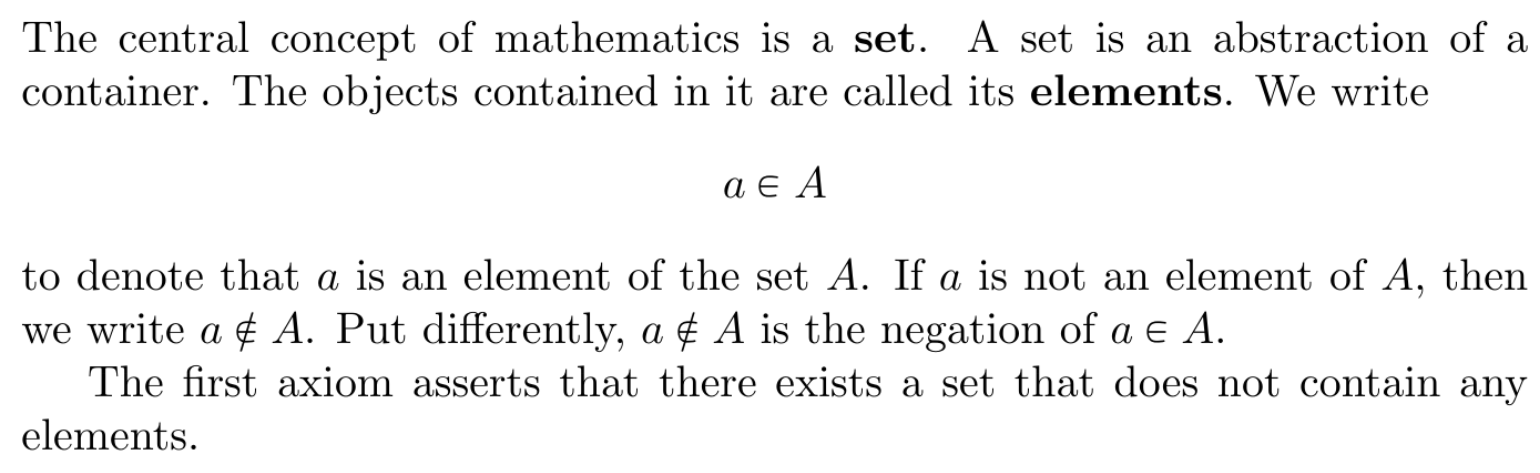
Singleton set

set with only one element, {a}

empty sets are not equal to singleton sets with one emtpy in it

set equivalency

subsets

power set

Power sets include subsets like the extreme empty, elements in the set, and entire set. 

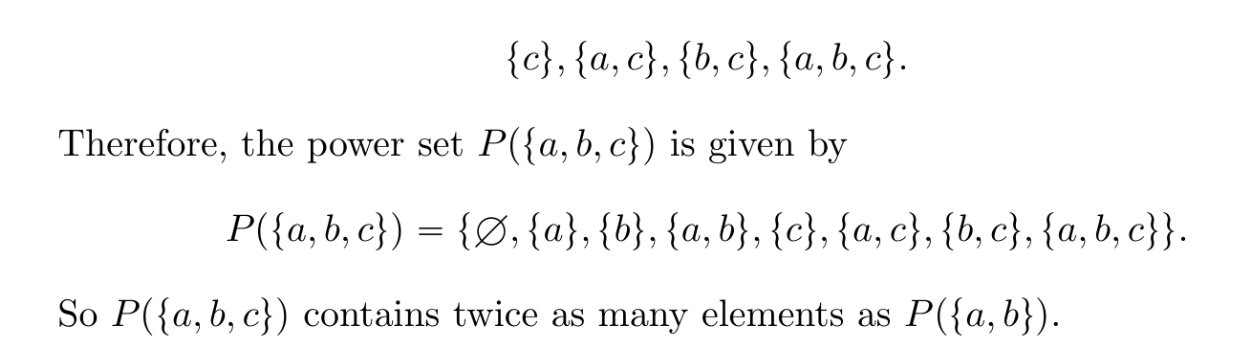
intersection set

the intersection contains elements from both sets A and B

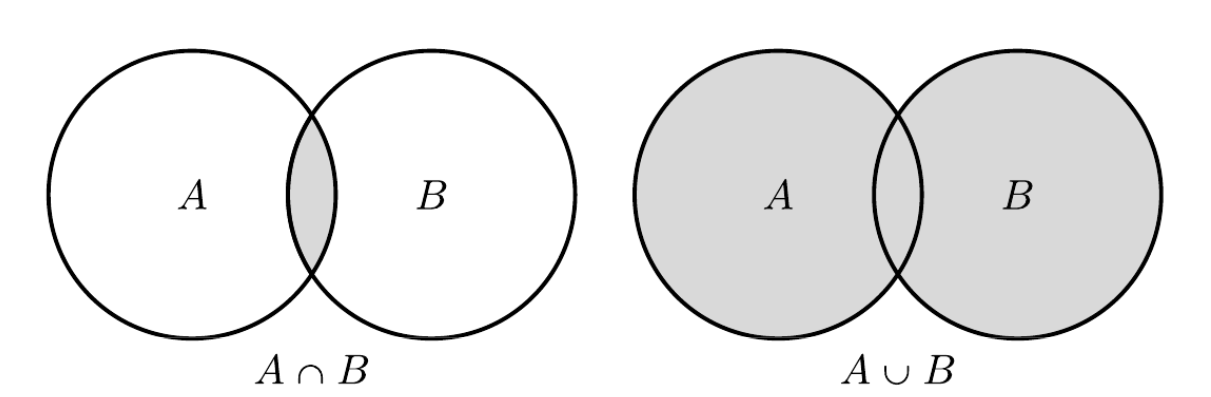
Disjoint

Sets are ____ when A^B = empty, which means there is no intersection

set union

when a set is made up of multiple steps and has the elements of both! For example, H = A U B so H is a union of A and BD

Difference

When A-B, the solution x is in A, but it wont be in B.

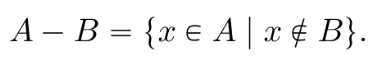
reflexive

xRx holds for all of x in A.

irreflexive

if xRx doesn’t hold for ANY x in A. if it only doesn’t hold for some, then it is not irreflexive. 

asymmetric

if (a,b) is in the relation, then (b,a) can’t be true. (a,a) also can’t be true.

Bob is the parent of chris. Chris cannot be the parent or bob, and can’t be his own parent…

“<“ is a asymmetric relation.

antisymmetric

• for every element (a,b) there is element (b,a) and in the pairs, a=b

• if ab is there and ba is there and b is not equal to a, then it’s not antisymmetric

  • if ab is there and ba is not there, then relation is antisymmetric, also asymmetric. 

symmetric

xRy implies yRx, has (1,3) and (3,1)

transitive

in x,y,z

xRy, yRz, xRz

Proof by contradicton

if not q then not p