Chapter 12 Notes: Indirect Proof (Symbolic Logic)

indirect proof

a type of proof used to derive the NEGATION of a statement

1. Assume the DENIAL of what you want to prove.

   1. Justification: AIP (assumption for indirect proof)

2. Try to derive a self contradictory statement.

3. Return to the left margin and discharge our assumption by writing the OPPOSITE of our assumption.

How is an indirect proof constructed?

d) All of the above

Which of the following is true?

a) P ● ∼P is necessarily true

b) If an assumption Q entails P ● ∼P, then Q is necessarily false.

c) If Q is necessarily false, then Q is necessarily true.

d) All of the above

d) All of the above

Which of the statements below, each of which is true about conditional proof, is also true about indirect proof?

a) You cannot end the proof on an indented line.

b) After your assumption is discharged, no indented line can be used to help justify any later line in the proof.

c) Multiple indented proofs can appear in a single overall proof.

d) All of the above. 

AIP

1, 2 DS

3, 5 MP

6, Simp

4, 7 Conj

4-8 IP

I don’t actually know if this is right because he didn’t go over this one, but I assume it is. 

Fill in the missing justifications in the proof below:
1. ∼Q

2. R ∨ Q

3. R ⊃ (S ● T)                   /T

   1. 4. ∼T                      (?)

   2. 5. R                      (?)

   3. 6. S ● T                (?)       

   4. 7. T                       (?)

   5. 8. T ● ∼T              (?)

9. T                                 (?)

Use indirect proof (at some point or other) for each argument below.

1. D ∨ C

2. D ⊃ C /C

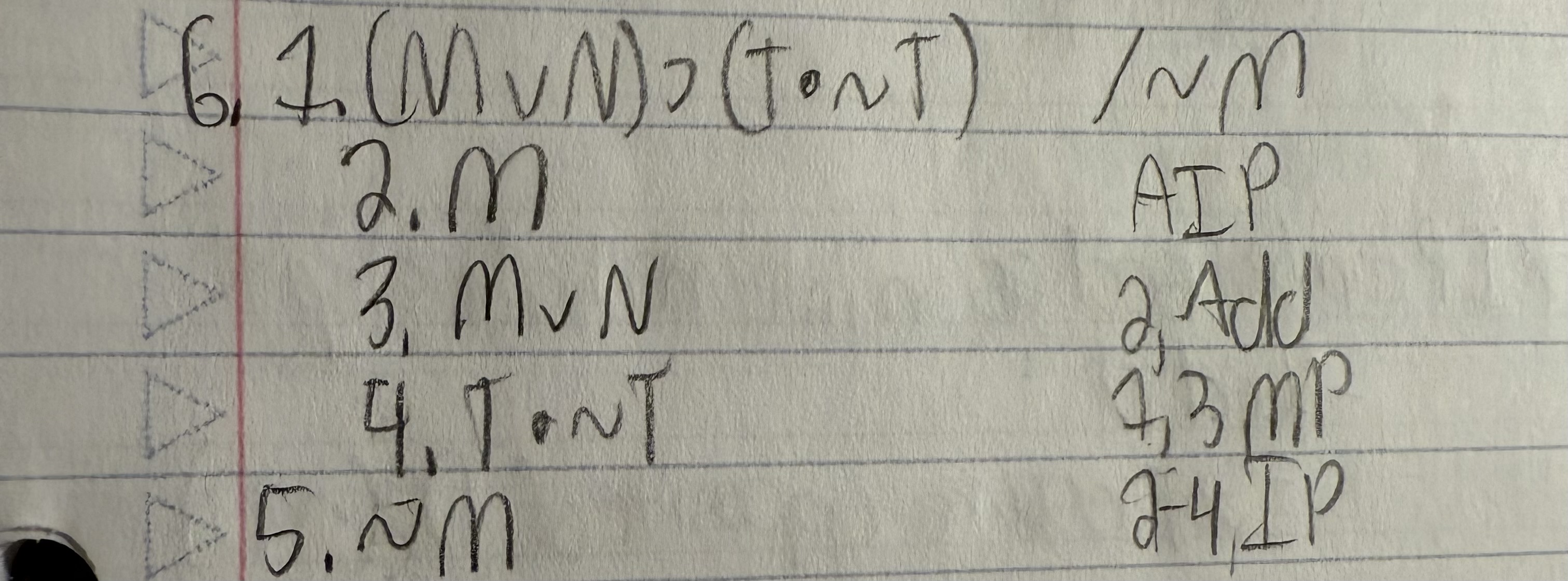
Use indirect proof (at some point or other) for each argument below.

1. (M ∨ N) ⊃ (T ● ∼T)                     /∼M

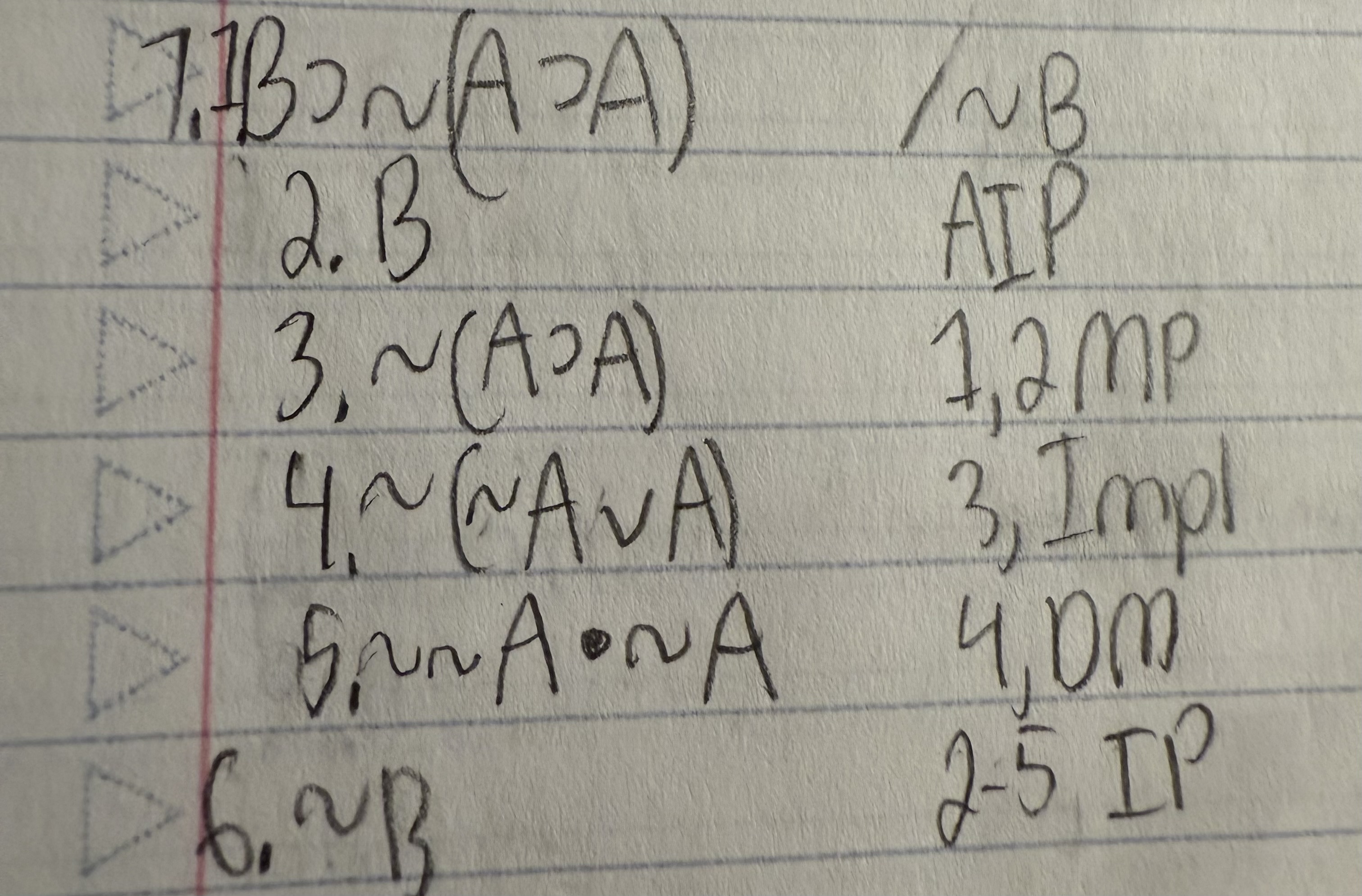
Use indirect proof (at some point or other) for each argument below.

1. B ⊃ ∼(A ⊃ A) /∼B

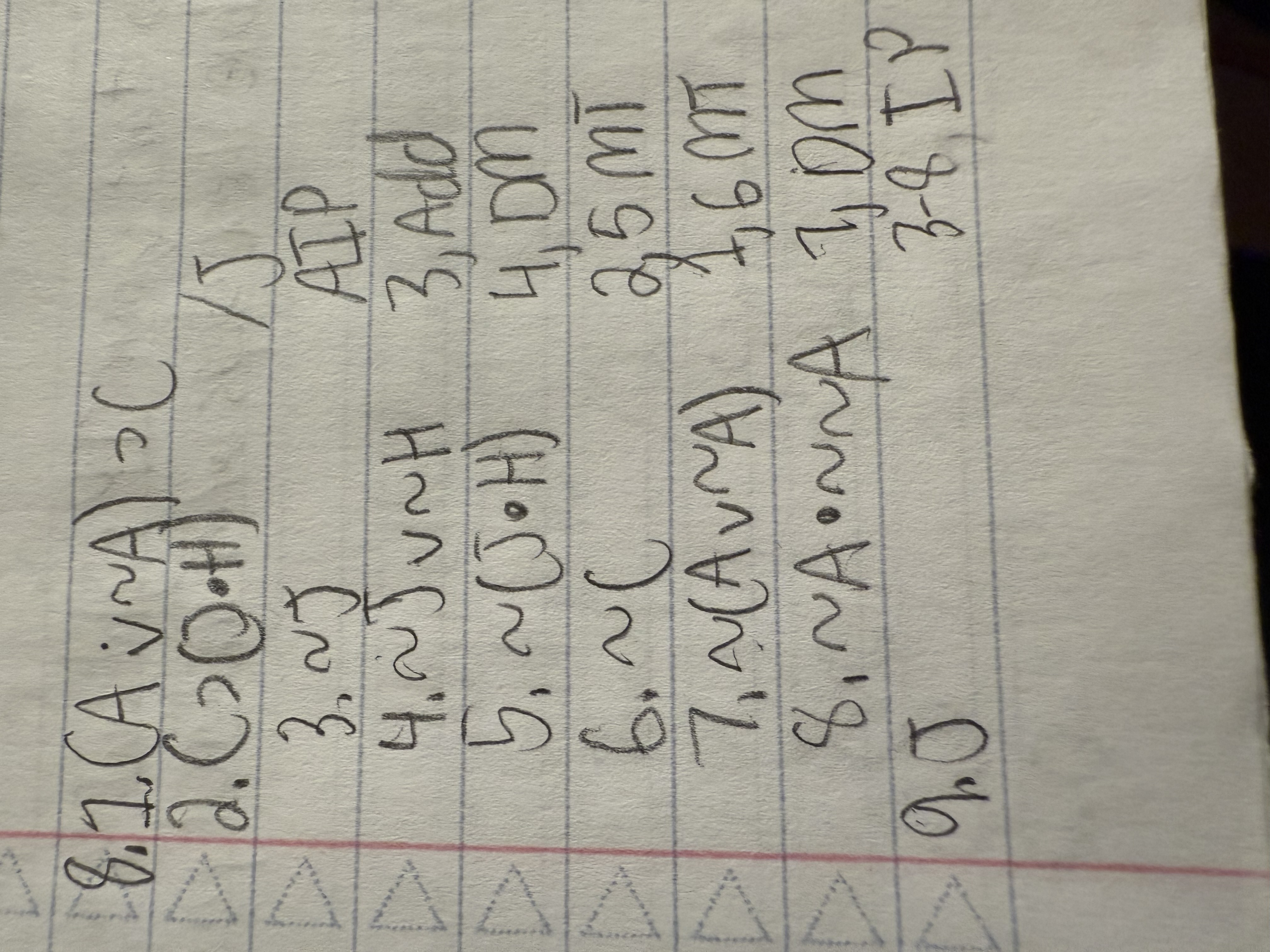
Use indirect proof (at some point or other) for each argument below.

1. (A ∨ ∼A) ⊃ C

2. C ⊃ (J ● H) /J

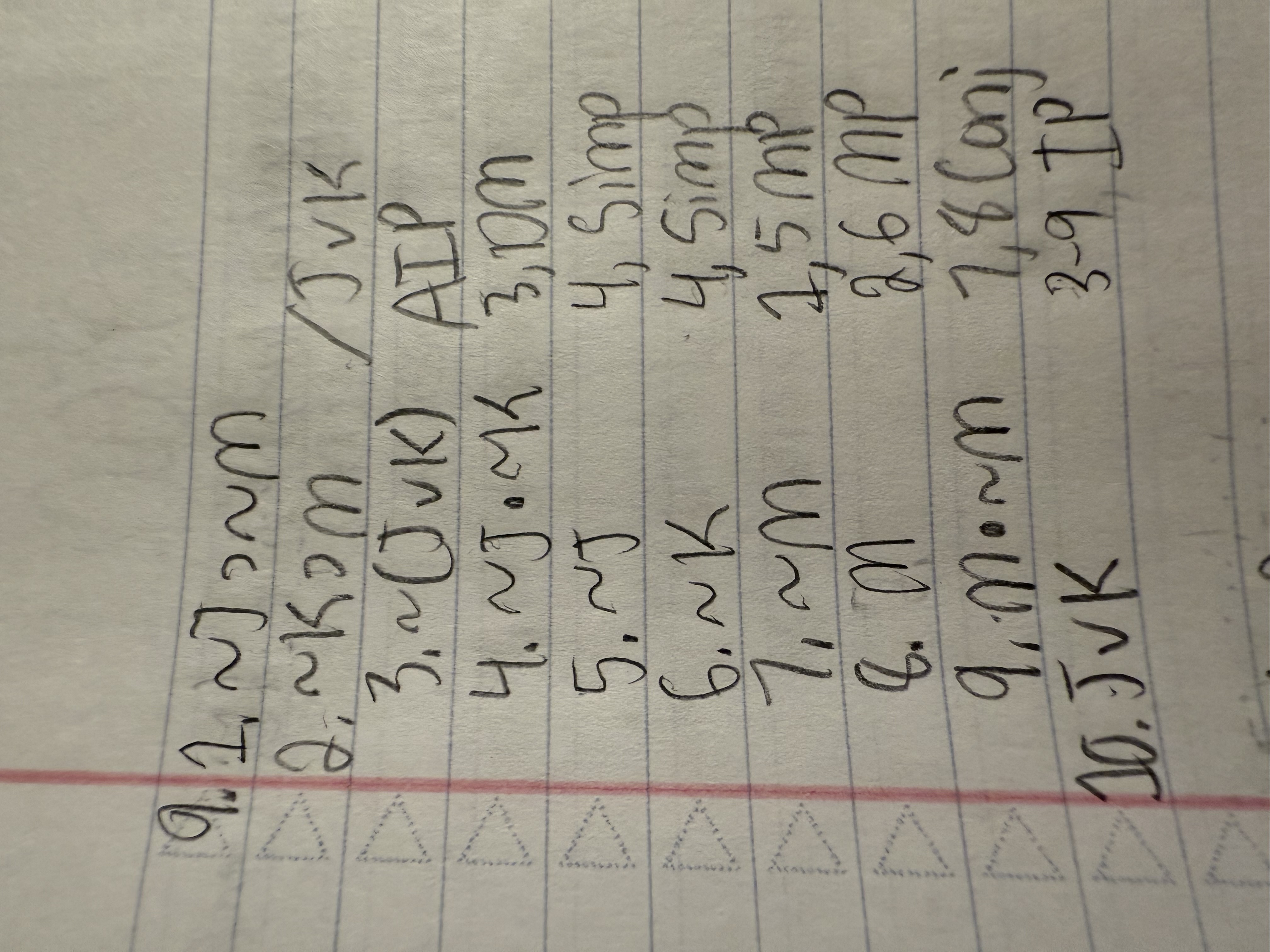
Use indirect proof (at some point or other) for each argument below.

1. ~J ⊃ ∼M

2. ∼K ⊃ M             /J ∨ K

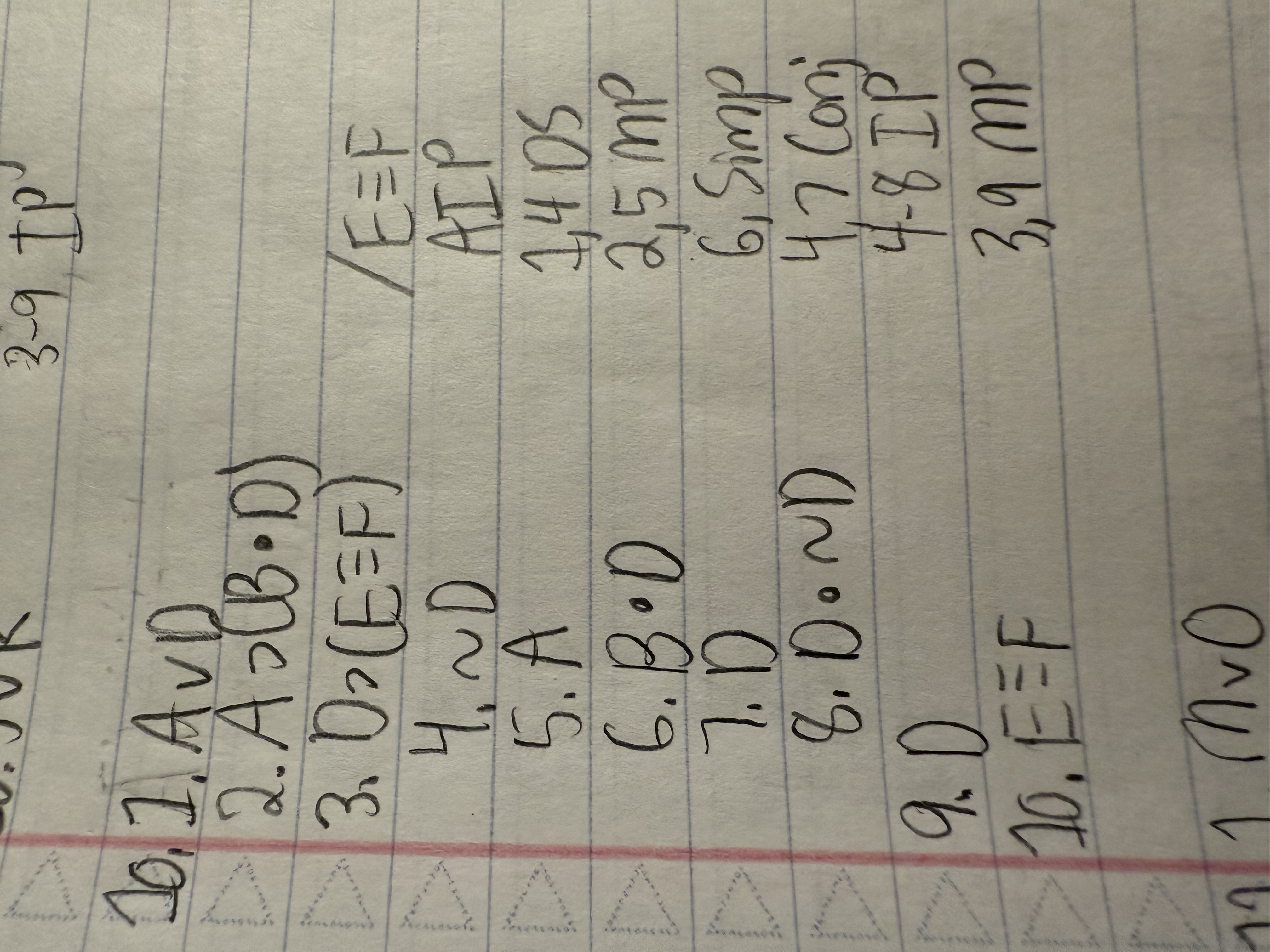
Use indirect proof (at some point or other) for each argument below.

1. A ∨ D

2. A ⊃ (B ● D)

3. D ⊃ (E ≡ F)                 /E ≡ F

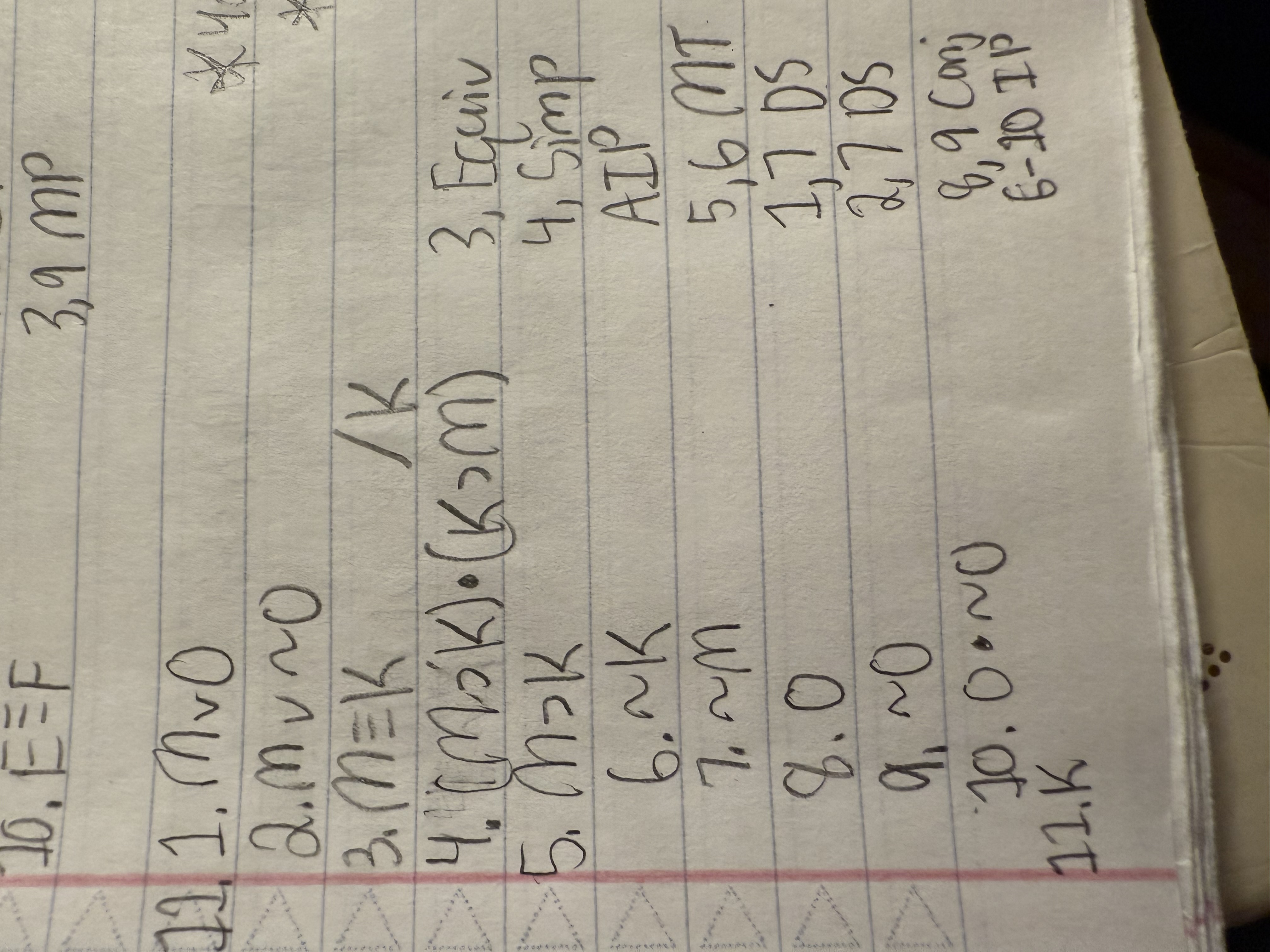
Use indirect proof (at some point or other) for each argument below.

1. M ∨ O

2. M ∨ ∼O

3. M ≡ K /K

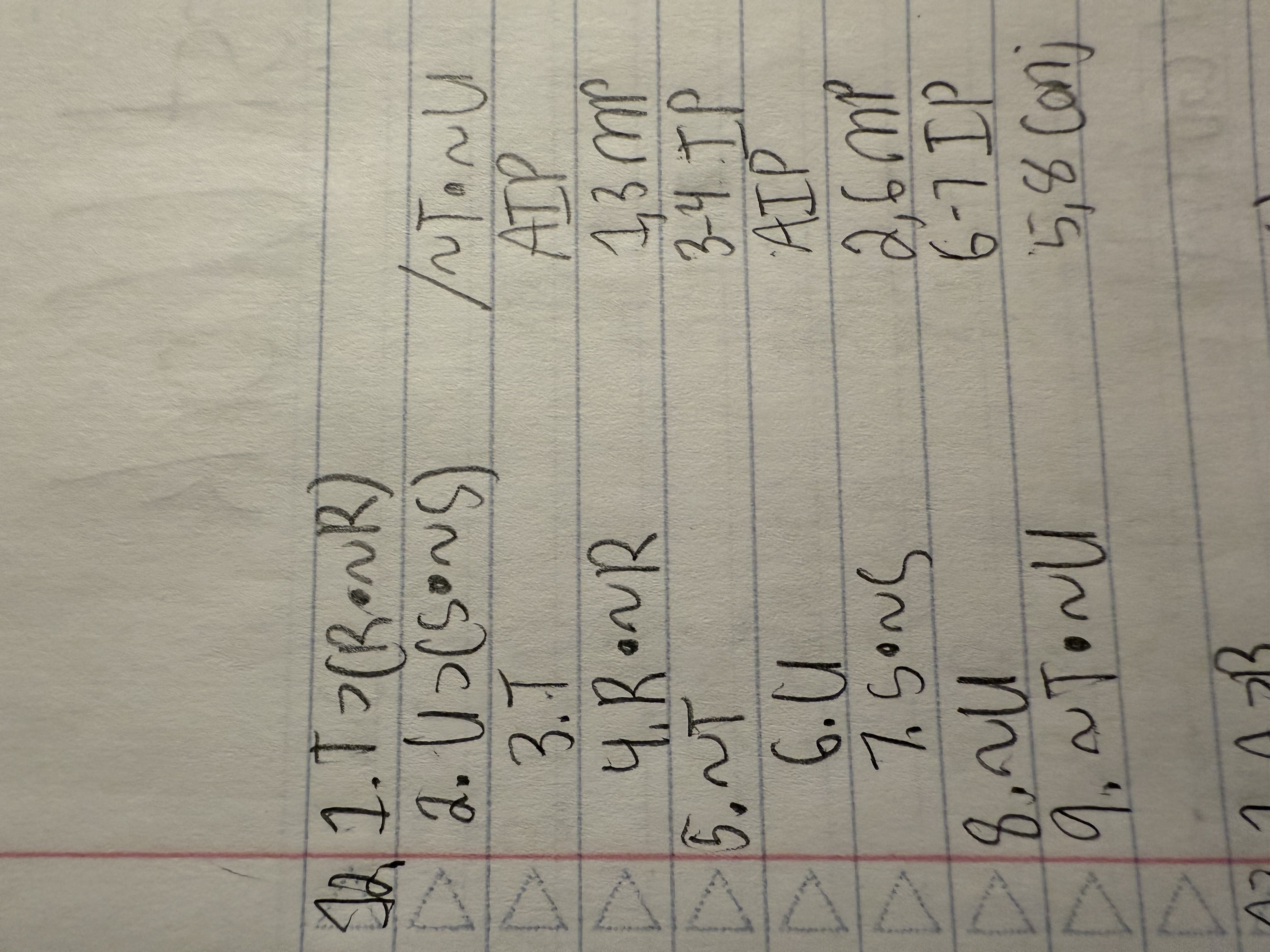
Use indirect proof (at some point or other) for each argument below.

1. T ⊃ (R ● ∼R)

2. U ⊃ (S ● ∼S) /∼T ● ∼U

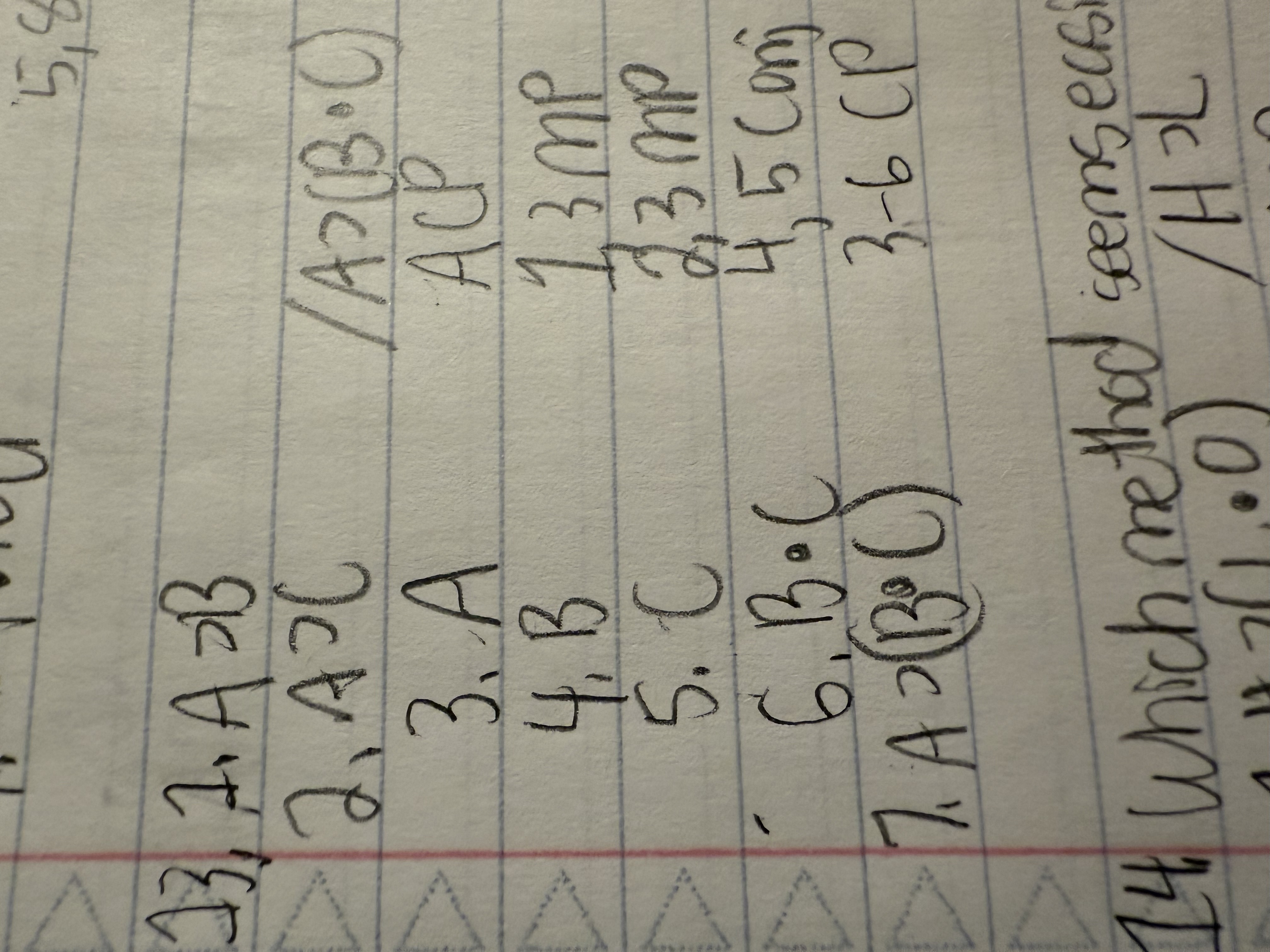
Use conditional proof (at some point or other) for the argument below.

1. A ⊃ B

2. A ⊃ C /A ⊃ (B ● C)

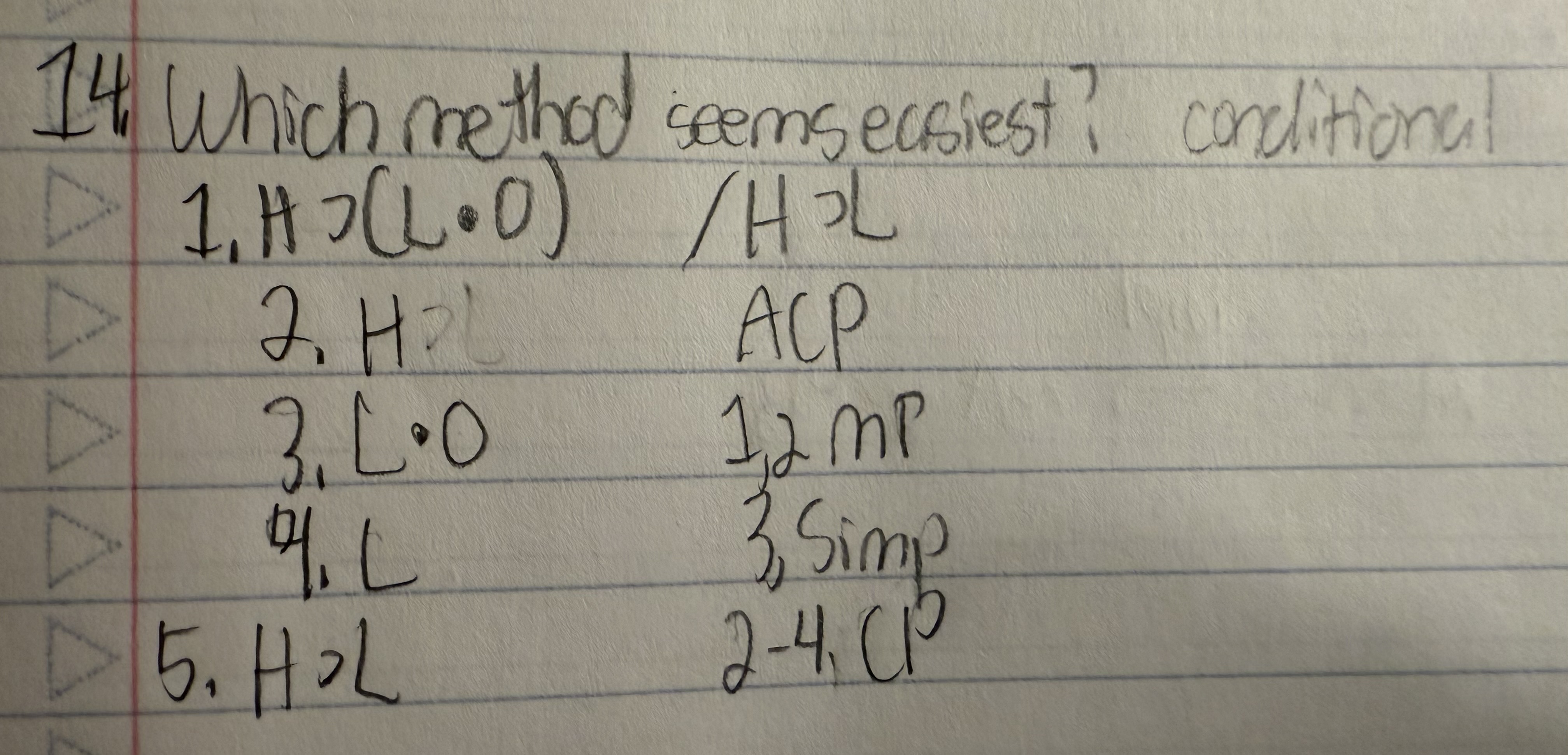
Which method (direct, conditional, or indirect) seems like the easiest way to prove the valid argument below?

1. H ⊃ (L ● O)          /H ⊃ L

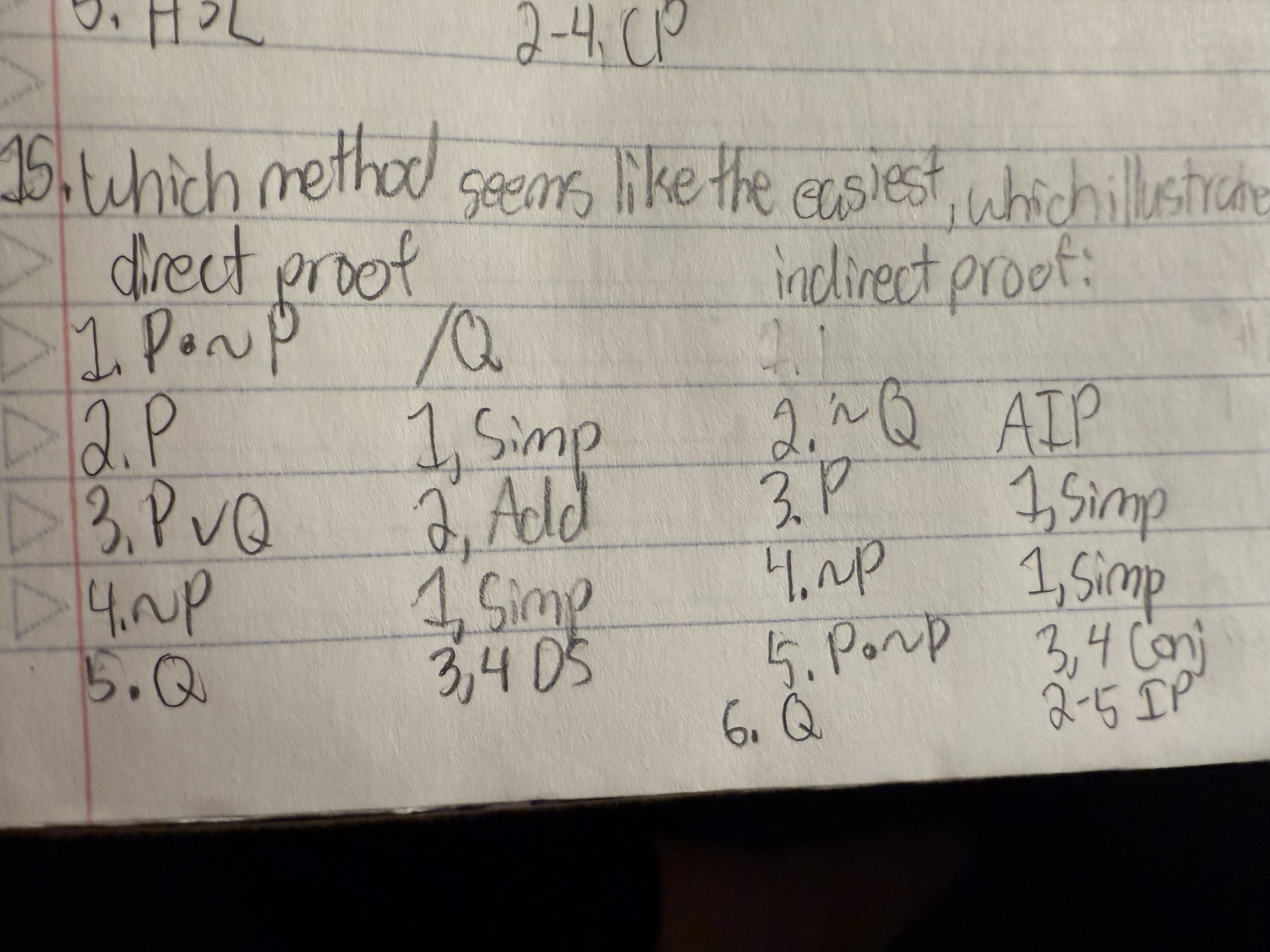
Which method (direct, conditional, or indirect) seems like the easiest way to prove the valid argument below, which illustrates the “principle of explosion” (that if a contradiction were true, then every statement would have to be true)?

1. P ● ∼P          /Q