Stats Exam 1

Numeric/Quantitative

Consists of numbers representing counts or measurements. These data types can be further classified into discrete and continuous variables.

Continuous

When the data can have infinitely many numeric values, where the collection of values is not countable, and can include fractions or decimals.

Discrete

When the data values are numeric and the number of values are countable/finite.
These values often represent whole numbers, such as counts of items or occurrences.

What is an example of a Discrete data measurement

Number of bananas in a bowl

Categorical/Qualitative

Data that consists of names or labels such as Gender, Traits and Names of places on Earth
(They can’t be numbers representing counts or measurements)

Nominal

A type of categorical data that represents different categories or groups without any intrinsic ordering, such as gender, race, or the names of countries.

Ordinal

A type of categorical data that represents categories with a specific order or ranking, such as levels of education or satisfaction ratings.

An example of a Ordinal Data point is

A satisfaction rating, such as on a scale from 1 to 5.

Population

The entire group of individuals or items that we want to draw conclusions about in a statistical study. (can be infinite or finite)

Sample

A subset of the population selected for analysis in a statistical study, used to make inferences about the larger group.

Sample Size

The number of observations or data points included in a sample, essential for achieving accurate and reliable statistical analysis.

Who is the population and the sample in this reading

A research study in 2025 titled “Banana bowl problem solved” talks about the maximum number of bananas a 10 inch diameter bowl could hold. Researchers tested 1000 different bowls filled with various different bananas to find the optimal packing size

The Population is the maximum number of bananas. The Sample is the 1000 bowls

Parameter

A numerical quantity that describes a characteristic of the population.
- This typically talks about everyone, all, or a known fact that doesn’t come from a sample (EX: there are 50 state capitols in the US)
- An example of this would be a proportion of all US residents who support the death penalty

Statistic

A numerical quantity that describes a characteristic of a sample
- This talks about a survey, study, or sample
- An example of this would be talking about a proportion of something, not all

Difference between a Parameter and a Statistic

A Parameter is more general with how it sites its info (talks about ALL)
A Statistic is more precise and concrete with it’s estimation (talks about a GROUP of ALL)
An example of the difference is this

Variable

Any characteristics, number or quantity that can be measured or counted.
(In a data set these are the Columns)

Data

Numerical or qualitative descriptions of the objects that we want to study

Experimental unit/Case

Object or thing that is being tested on/ having data collected
These are generally the Rows in a data test

Simple Random Sampling

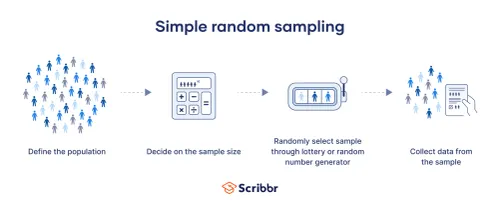
A type of sampling that consists of a random amount of individuals that have an equal chance of being selected
- Lottery method

- RNG

Stratified Sampling

A type of sampling that involves dividing a population into similar subgroups (called strata) then randomly selecting samples from each stratum

Cluster Sampling

A type of sampling where a population is divided into groups, then a random selection of these groups are chosen and all get sampled

Systematic Sampling

A type of sampling where the sample members from a population are chosen via selection in a fixed interval

- Example: Select every fourth dog on a park (This is called the sampling interval, calculated by dividing the population size from the desired sample size)

What is the difference between a Experimental Study and a Observational Study?

In a Experimental Study, the researcher manipulates a certain factor or treatment

In a Observational Study, the researcher can only watch without making their sample do things they want

What are the cons of an Observational Study?

Randomization

Experimental units are assigned to random treatments by chance

This is good because it reduces confounding and bias

Difference between being in a Control group and not

The major difference comes in who receives the treatment

Those not in the Control group receive the treatment, while those who are do

Placebo

A treatment that lacks the active ingredient of the treatment being tested

This is used to see the reaction of those who took it vs those who didn’t

Blinding

Participants are not told which treatment they are receiving

This helps reduce bias

Explanatory Variable

The variable that is changed or manipulated by the researcher to observe its effect on an outcome variable.

- It is also known as the independent variable.
- Example: In a study on the effect of fertilizer amount on plant growth, the amount of fertilizer is the explanatory variable.

Confounding Variable

A variable in a study that is related to other variables, affecting the relationship between those variables

- Example: Ice cream sales are associated with drowning

Confounding Variable problems

False reasons for why something is happening
Summer heat = more ice cream sales and drowning is valid
Ice cream sales = more drowning is not valid because Ice cream sales going up doesn’t mean drowning will be more relevant

Lurking Variable

A variable that is not the explanatory or response variable but has a relationship with both
- Example: A scientist studies the effects of a diet and exercise on a person’s blood pressure. The lurking variable that can affect blood pressure are whether a person smokes or is stressed

Selection bias

When some groups are left out of the processes in choosing the sample

Nonresponse

When an individual for a sample isn’t contacted or refuses to participate

Response bias

A systematic pattern of incorrect responses
An example of this Wording of a question (How Amazing was your stay?)

Response Variable

The variable that is measured or observed and is expected to change in response to the manipulation of the explanatory variable.

- It is also known as the dependent variable.

- In a study on the effect of fertilizer amount on plant growth, the plant growth is the response variable.

Block Design

A technique used in experimental designs to reduce the impact of variability by grouping similar cases together

Variation

The primary reason for using blocking when designing an experiment to reduce

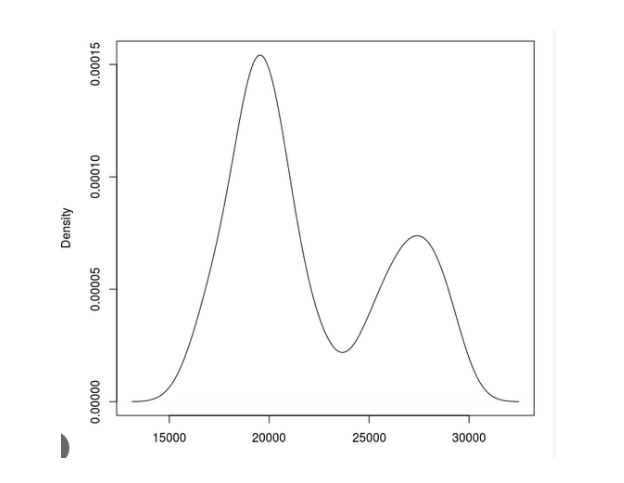
Bimodal

Describes a distribution of values that has two individual centers of population

Mean

The average value of all the data
Calculated by adding all the data then dividing it by the number of data points

Median

The midpoint of the distribution

(n+1)/2

How to find the Median

• If the number of data is odd
  1. The median is the center of the ordered list
  2. It will be a whole number

  3. (n+1)/2 is the position of it
  

• If the number of data is even

  1. The median is the average of the two center observations of the ordered list

  2. Will likely not be a whole number

  3. Between n/2 and (n+1)/2 is where it’s located

Quartile

From Min to Max
Min is the minimum value

Q1 is 25% of the data, position is located on the data by calculating (1/4) * (n+1)
Q2 is 50% of the data, also known as the median

Q3 is 75% of the data, position is located on the data by calculating (3/4) * (n+1)
Max is the maximum value

Interquartile range (IQR)

The spread of half your data

Calculated by Q3 - Q1

When to use Mean and Standard Deviation for data

Only for reasonably symmetric distributions that have NO OUTLIERS

When to use Median and Interquartile range for data

When describing a SKEWED distribution or one WITH OUTLIERS

Frequency Table

Creates intervals of values of equal width that cover the all the data along with corresponding frequency in the interval

Class Width

Used in Frequency Tables

Found by calculating (Max - Min)/ n

Make sure to round up or down accordingly to make data cleaner

Histogram

Used to show the distribution of a Quantitative variable by using bars whose height represents the number of individuals

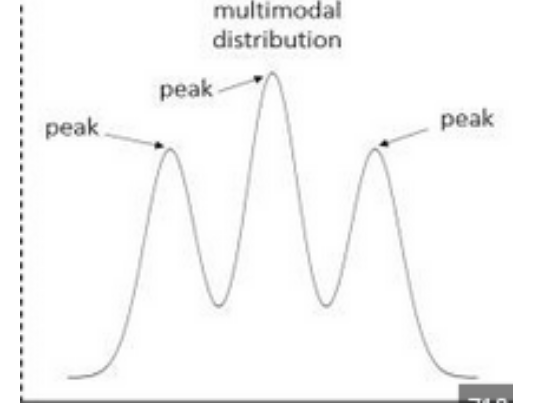
Multimodal

A set of data that has more than 2 values that occur with similar frequency

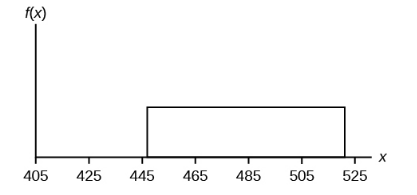
Uniform

A type of probability distribution in which all the outcomes are equally likely

What graphs to use for Quantitative Variables

1. Frequency Tables/Distribution

2. Histograms

3. Boxplots

4. Stem and Leaf Plots

5. Dot Plots

What graphs to use for Qualitative Variables

1. Frequency Tables/Distributions

2. Bar Graphs

3. Pie Charts (Don’t actually use)

Frequency

The number of times each category shows up in a data set (for a table)

Relative Frequency

The fraction of times each category shows up in the data set (for a table)

Cumulative Frequency

The total number of observation up to and including that class
Effectively Relative Frequency but you add the previous values to it

Using Mean and Median to find skewed distributions

In a Skewed distribution,
the Mean is usually Farther out in the tail than the Median

Mean out, Median in
Me go out, Med go in

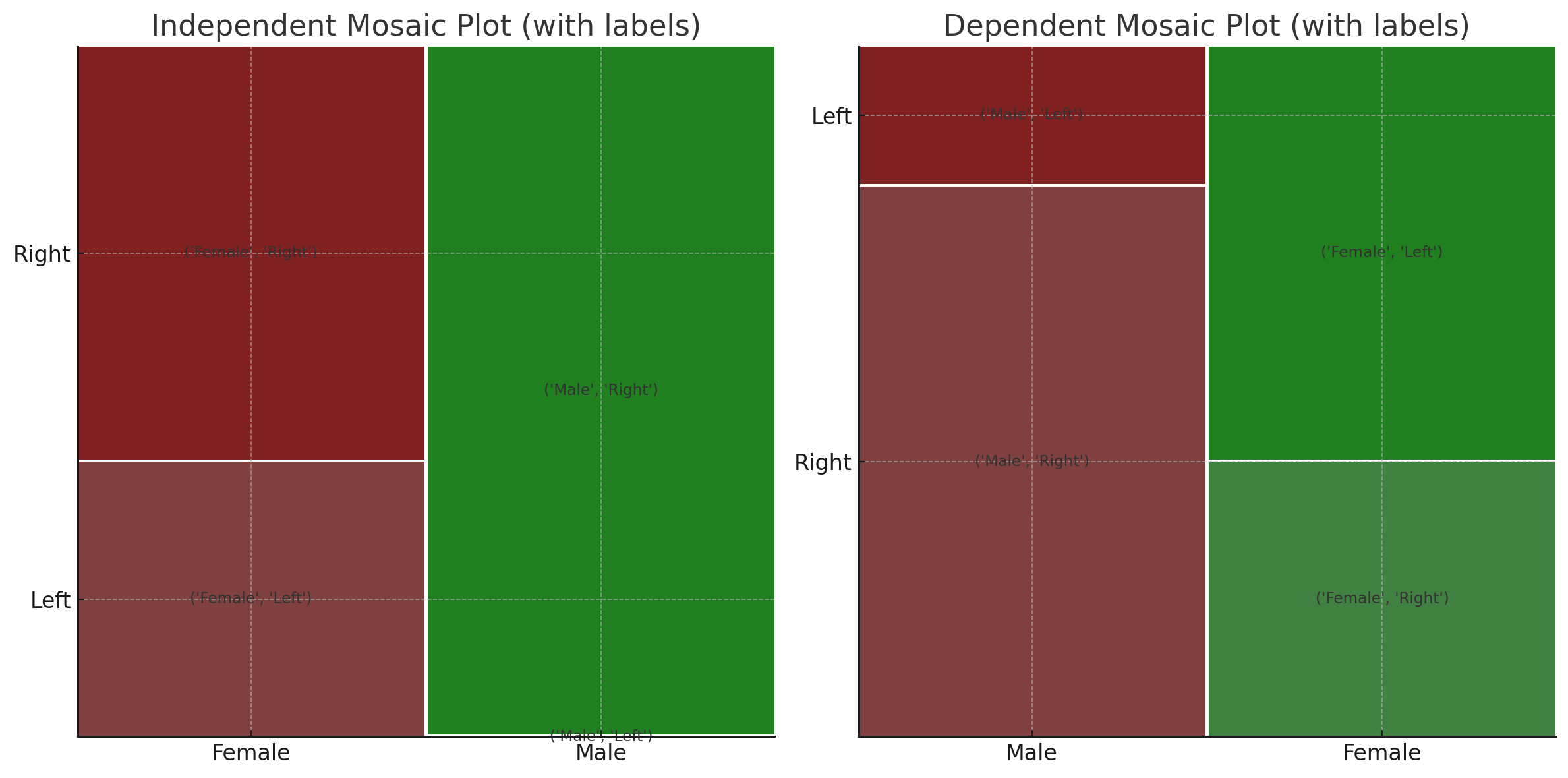
Independent vs Dependent in Mosaic Plots

• Independent

  • When the data lines up well, it’s independent

• Dependent

  • When the data is varied, then it’s dependent

Upper bound

Q3 + 1.5(IQR)

Lower bound

Q1 - 1.5(IQR)

Rule of thumb Upper bound

mean + 2(std dev)

Rule of thumb Lower bound

mean - 2(std dev)