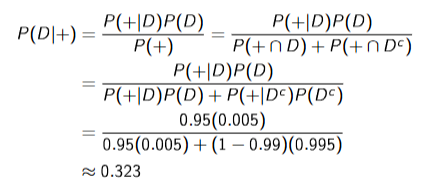4. Probability

Independent Events

AnB = P(A) * P(B)

p(A|B) = P(A)

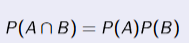
Dependent Events

AnB > P(A) * P(B)

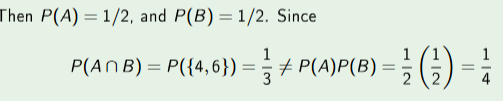
Complement of an Event

A^{c}

Mutually Exclusive

P(A U B) = P(A) + P(B)

Implies dependence

Pairwise Mutally Exclusive

P(A1 U A2 U A3) = P(A1) + P(A2) + P(A3)

E.g Outcome of single coin toss

Additive Law of Probability

P(A∪B∪C ) = P(A)+P(B)+P(C )−P(A∩B)−P(A∩C )−P(B∩C )+P(A∩B∩C)

Conditional Probability

when P(B) > 0

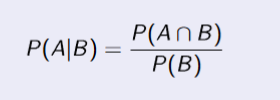
Partition

B1 U B2 U B3 U B4= S

All shoudl be mutually exclusive

Bayes Theorem

Probability of Bi given A happened

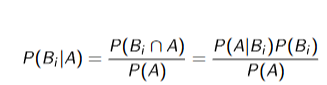
Sensitivity (False Positive)

Probability that the test is positve, given that the person has the disease

Specificity (False Negative)

Probability that the test is negative, given that the person does not have the disease

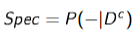
Prevalence

Number of people who currently have the disease / number of people in the population.