G10 Q3 Math Geo sequence + Log + Trig Test Bank
1/47
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
48 Terms
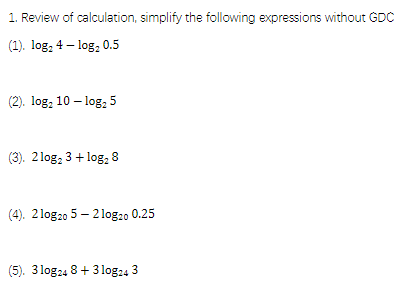
1.) 3
2.) 1
3.) 2log 2( 3) +3
4.) 2
5.) 3
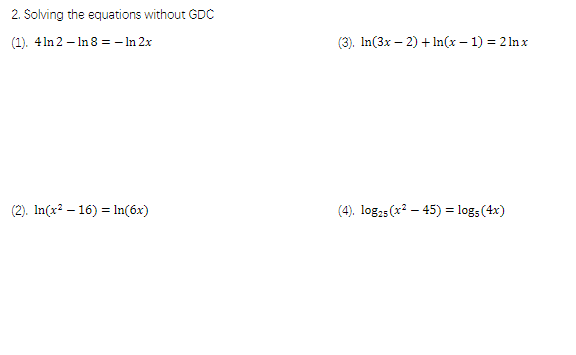
1.) x=1/4
2.) x=8
3.) x=2
4.) no valid solutions

1.) 2a+1/b
2.) 2ln3/ln5
4a ln(15) = (a+2) ln 81
solve for a

4.1.)
X-Intercept: (1,0)
Pass Point: (e,1)
Vertical Asymptote: x=0
Range: (-inf, +inf)
Domain: (0, +inf)
2.) 2(ln -2(x+(1/2)-2)-1)
3.) Vertical stretch by 2
Reflect over x axis
Translate (-3, -1)

f(x)
Domain: (-inf, +inf)
Range: (-2, +inf)
Horizontal Asymptote: y = -2
f-1(x)
Domain:(-2, +inf)
Range: (-inf, +inf)
Vertical Asymptote: x = -2
X intercept: (8,0)
Y intercept: (0, -0.6989)

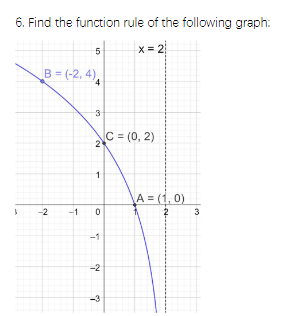
f(x)=log sqrt2 (-x+2)

1.)k = 500
2.) 10^6

I = 10.2
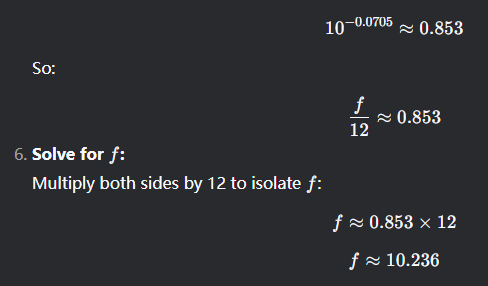

1.) R(200A0) = log(200A0/A0) = log(200) = 2.301
2.) Find (A1/A2)
6.8-5.8
10^0.9
3.)
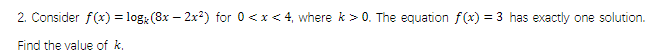
k = 2
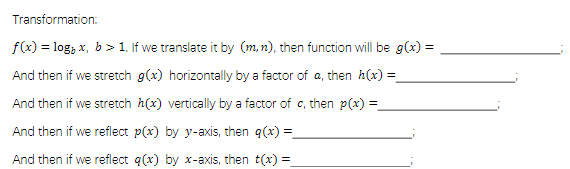
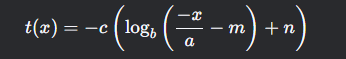
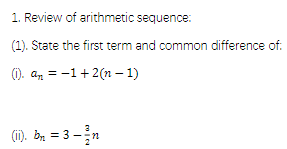
i) a1: -1 CD: 2
ii) a1: 3/2 CD:-3/2


an = 11-3(n-1)
an = log p (b) + (log p (a))²

i) First term: -2 CD:(1/2)
ii) First term: =-2/3 CD:(-1/2)

an = a1 * r^(n-1)
i) an = 2 × 2^(n-1)
ii) an = -2 × (1/2)^(n-1)
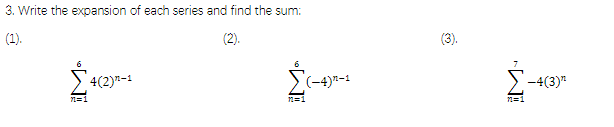
1.) 4+8+16+32+64+128
2.)
3.) -13116

1.) 5 sigma n=1 1/5 × (1/2)^(n-1)
2.) 6 sigma n=1 4 * (-3)^(n-1)

7 Terms

11th term 2187
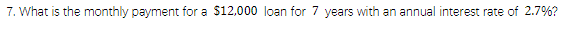
First Convert the Annual interest and Annual pay time to months
Time - r: 7 × 12 = 84
Interest per month - n: 0.00225
Use the Loan Amortization Formula
Then solve for the monthly payment amount M


First Year: $476.72
Total Pay: $3167.86

1.) First one CD: 5
2.) Last one CD: ½
3.) 1/64

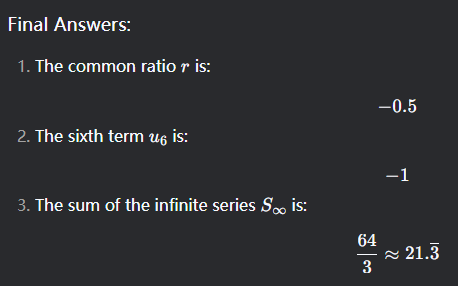

Use Infinite series function
Solve for R algebra substitution


1) Explain it in plain words
2) Use the finite sequence formula
-First term a = 4*(0.8)
-Common ratio = (0.8)
-Don’t forget to add 2 meters
To find the total distance travelled in terms of n
3) Use infinite series


1i) r = (an)/(an-1)
Thus r = 4/(k-4) and r = (k+2)/4
(k+2)/4 = 4/(k-4)
ii) Cross multiply and solve for k
4 × 4 =(k-4)(k+2)
Simplify and rearrange to get
k^2−2k−24=0
2i)Use quadratic formula to solve for k
k = 6 k = -4
ii) Find all possible values of r
Substitute k into the r = equations from before
r = -0.5 and r = 2


Finite Series Formula Sn = (a1(1-r^n))/(1-r)
Infinite Series Formula Sn = a1/(1-r)
-1 < r < 1
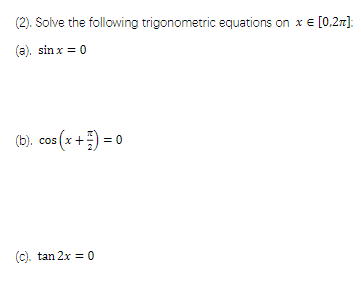
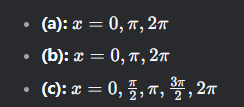
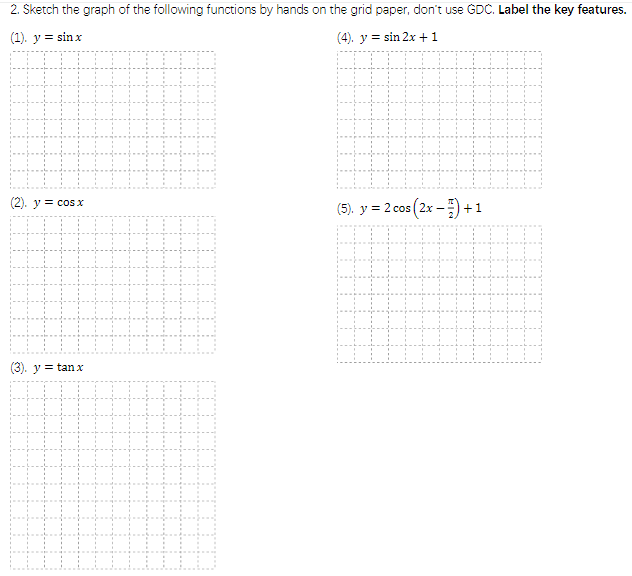
Domain: IR # Range: [-1, 1] # Max: (π/2, 1) # Min: (3π/2, -1)
Domain: IR # Range: [-1, 1] # Max: (0, 1) # Min: (π, -1)
Domain: IR # Range: IR # Asymp x = πk # (0, πk)
Domain: IR # Range: [0, 2] # Max: (π/4, 2) # Min: (5π/4, 0)
Domain: IR # Range: [-1, 3] # Max: (π/4, 3) # Min: (5π/4, -1)
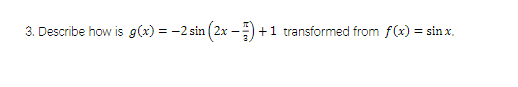

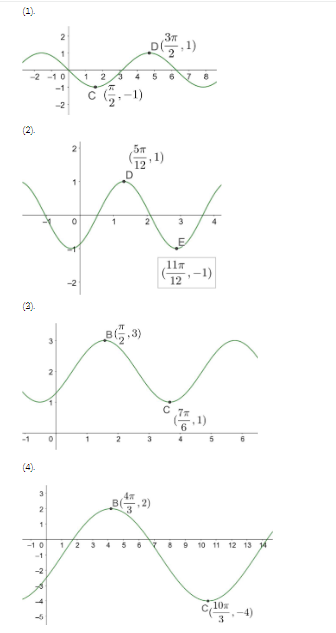
Find function rule
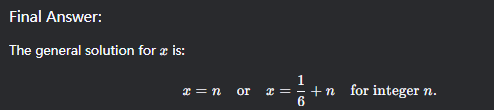
1.) Sin(x-π) or -Sin(x)
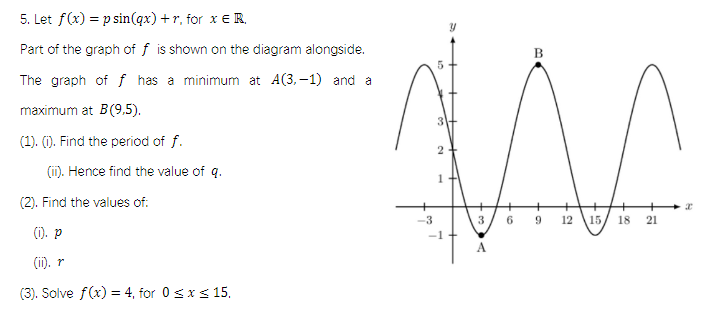
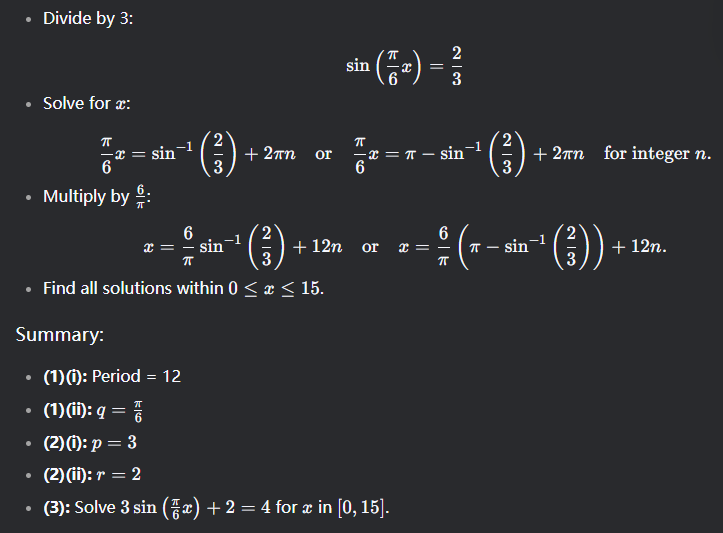

2.) x = π/24 + πk
x=5π/24 + πk
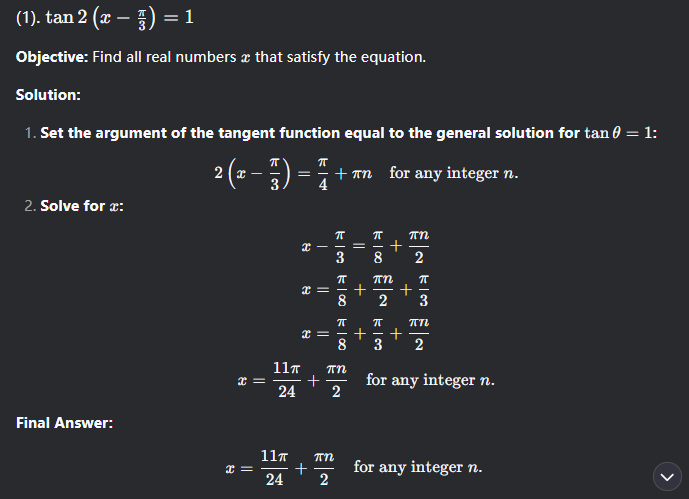
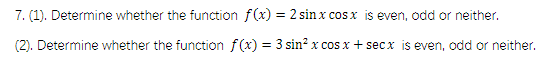
(1): The function f(x)=2sinx * cosx is odd.
(2): The function f(x)=3sin^2x * cosx + secx is even.

y=7cos(3/πx)

1.) h(θ)=8tanθ
2.) Look pic
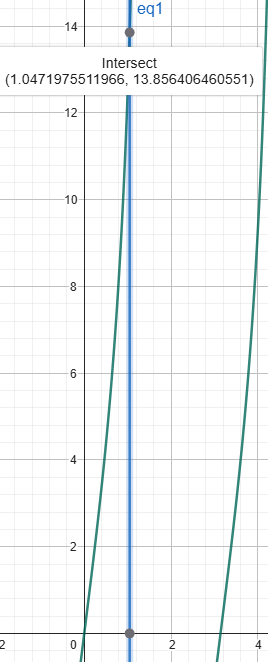

(3). 3cos(24π/149 t) +5





The vertical shift D is the average of the maximum and minimum temperatures.
D=(87+40)/2=63.5
The maximum temperature occurs in July, which is the 7th month.
For a cosine function, the maximum typically occurs at t=0t=0. Since the maximum is at t=7t=7, the phase shift CC is 7.
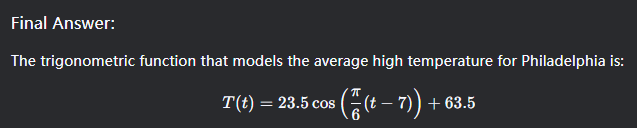

1.) 1.5M


(a): The period pp is 1/262 seconds.
(b): The frequency ff is 262 Hz.
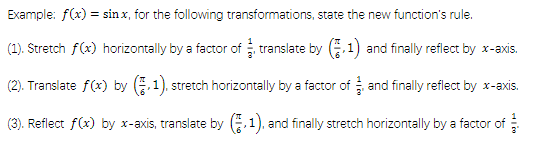
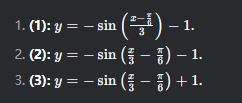


1/12
1/12 # ¼