Geometric optics

Key optic principles applied to orthoptic practice

Refraction

Passage of light from one optical medium to another of different refractive index. It results in bending of light rays, affecting how images are formed and perceived by the eye.

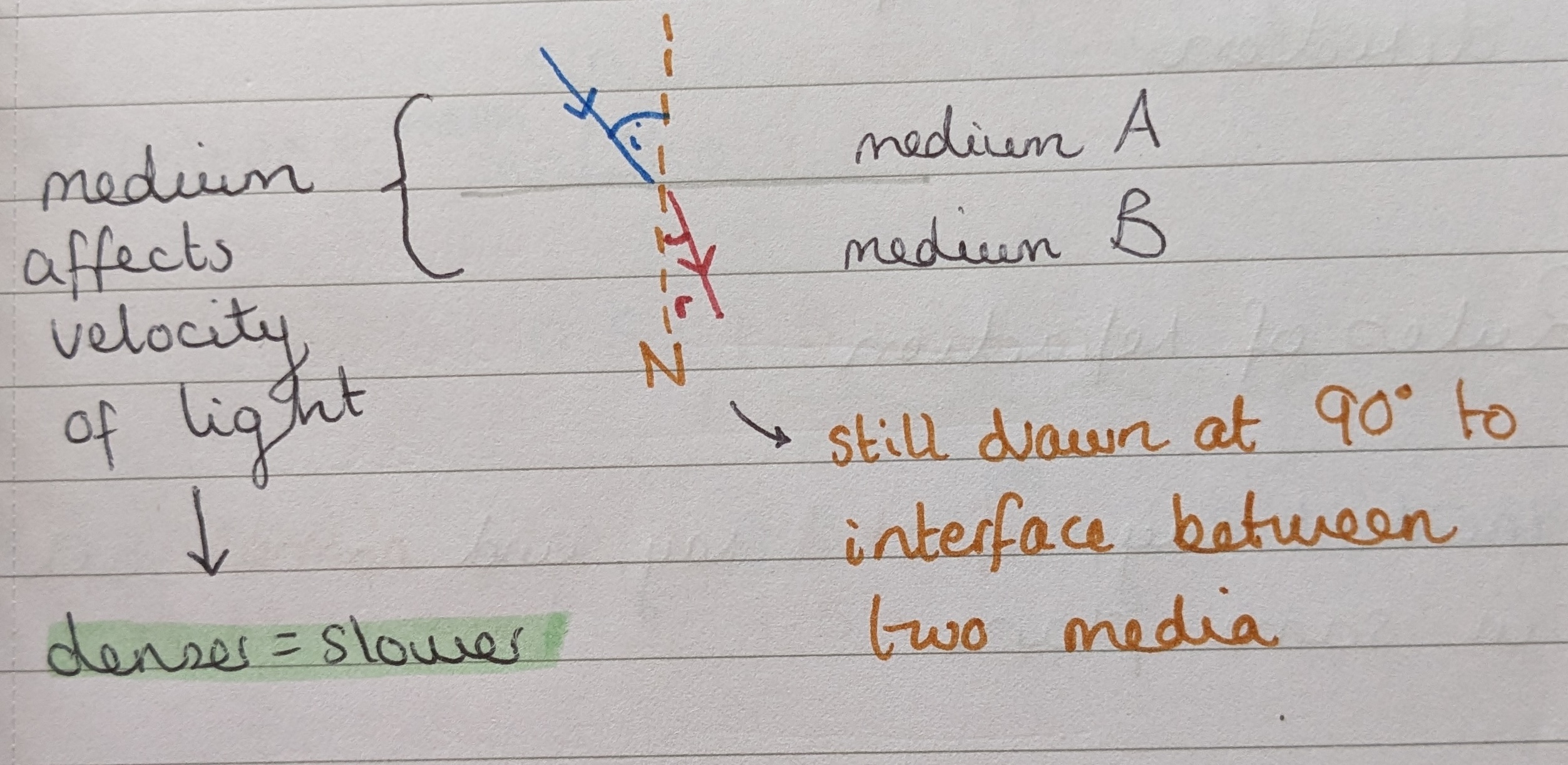
Refractive index

n = velocity of light in vacuum/velocity of light in medium

A higher refractive index creates more bend in the light rays.

In air, the refractive index can be considered as 1.

True or false - in refraction, the angle of incidence equals the angle of reflection?

False; this is only true for reflection, not refraction.

Snell’s law

Describes the relationship between the angles of incidence and refraction when light passes between two different media.

n₁ sin i = n₂ sin r

Where n₁ = refractive index of the first medium, i = angle of incidence, n2 = refractive index of the second medium, r = angle of refraction.

Calculate the angle of refraction (r ), where n₁ = 1.0, n₂ = 1.5, and i = 30^o

Step 1) Rearrange the formula for Snell’s law, using μ = n₁/n₂

sin i = μ sin r

Step 2) Plug in the values from the question, and simplify

sin (30) = (1.0/1.5) sin r

sin (30) = 1.5 sin r

0.5 = 1.5 sin r

Step 3) Solve for sin r

sin r = 0.5/1.5 = 0.3333

Step 4) Solve for r

sin^-1(0.5/1.5) = 19.5^o

r = 19.5^o

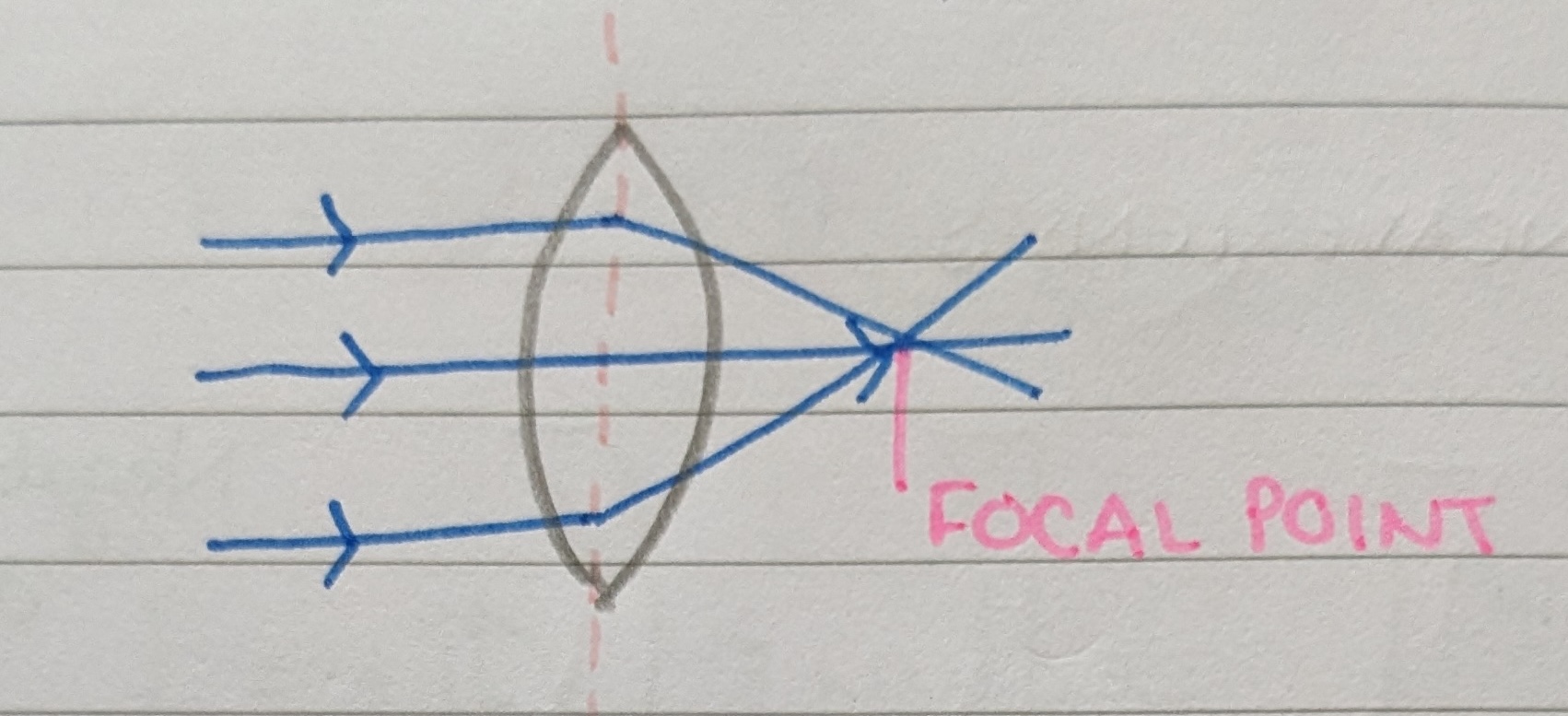
Do convex lenses converge or diverge light?

Convex lenses converge light rays toward a focal point, making them useful for magnifying images and correcting hypermetropia.

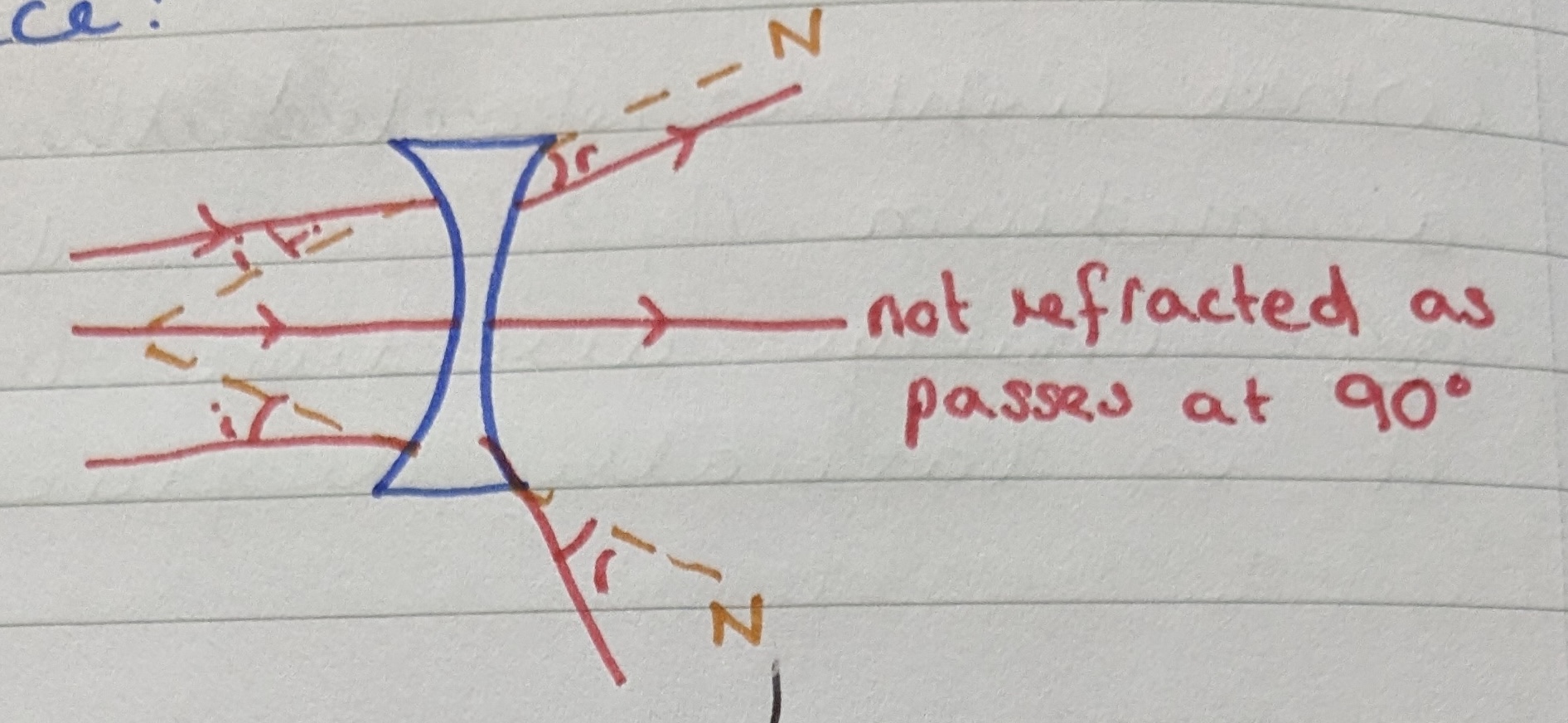
True or false - concave lenses converge light.

False, concave lenses diverge light rays, making them useful for minimising images and correcting myopia.

What is total internal reflection?

Total internal reflection occurs when light traveling through a medium hits a less refractive medium at an angle greater than the critical angle, resulting in no refraction and complete reflection.

Critical angle

The minimum angle of incidence at which total internal reflection occurs, specific to the refractive indices of two media.

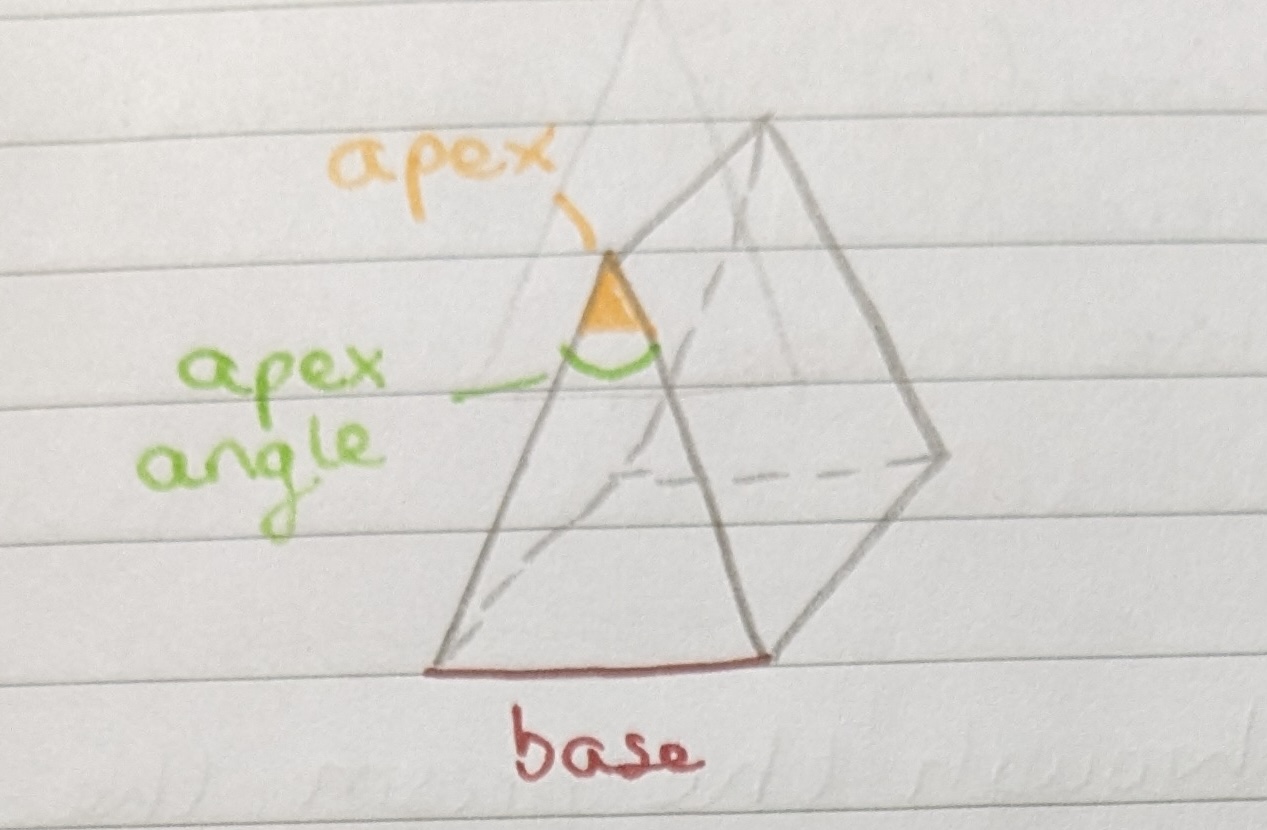
Prism

Two flat, polished, refracting surfaces placed at an angle to each other. Light is bent from the apex of the prism towards its base. The strength of a prism is measured in prism dioptres ^.

What are the components of this equation, used to calculate the power of a prism - P = tan v?

P = power, ^

v = angle of deviation

The angle of deviation is the angle between the original path of light and the path after passing through the prism.

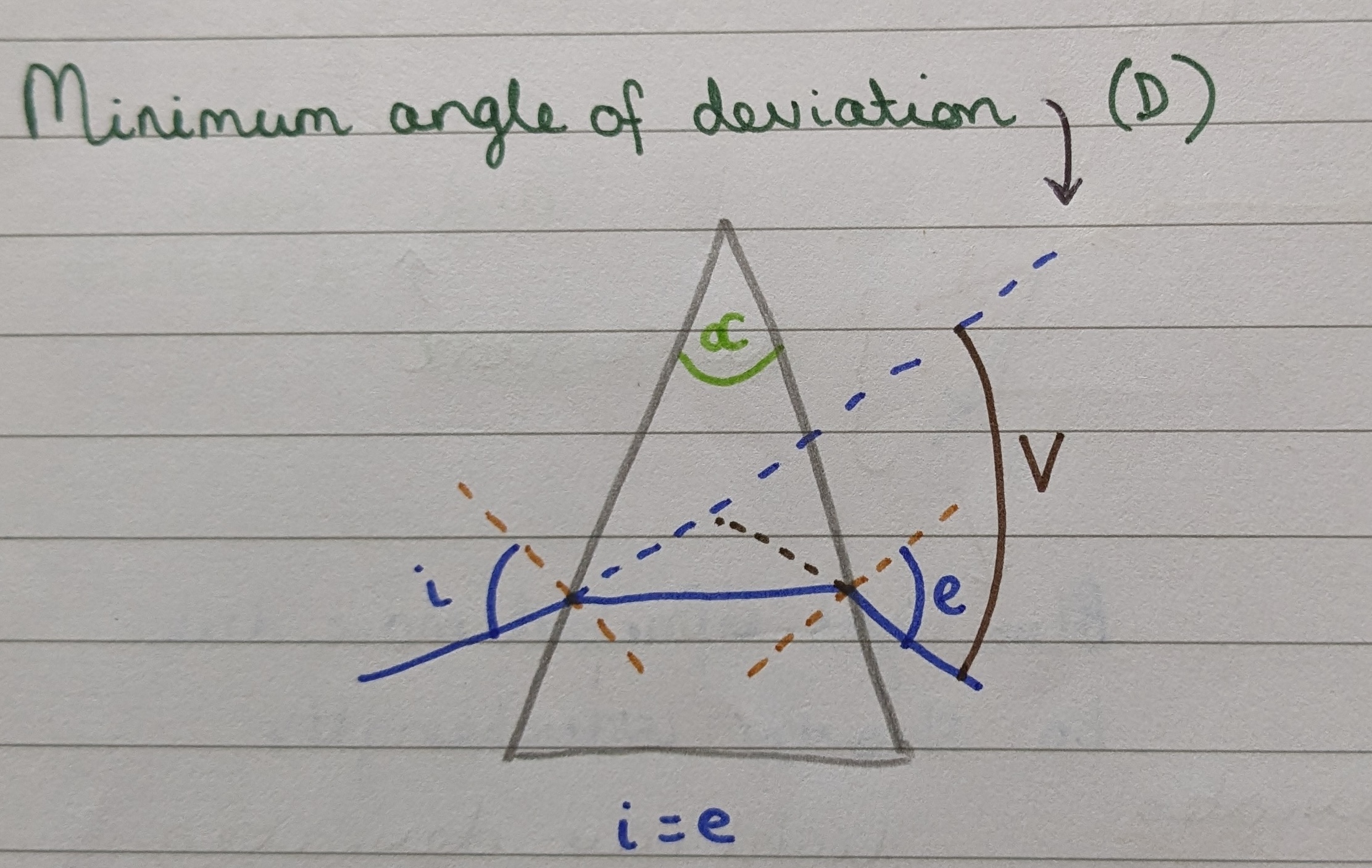
Minimum angle of deviation (D)

The smallest angle formed between the incident ray and the emergent ray when light passes through a prism, occurring when light passes symmetrically through the prism. This is the weakest position.

In thin prisms, the minimum angle of deviation (D) and the angle of deviation (v) can be thought of as equal.

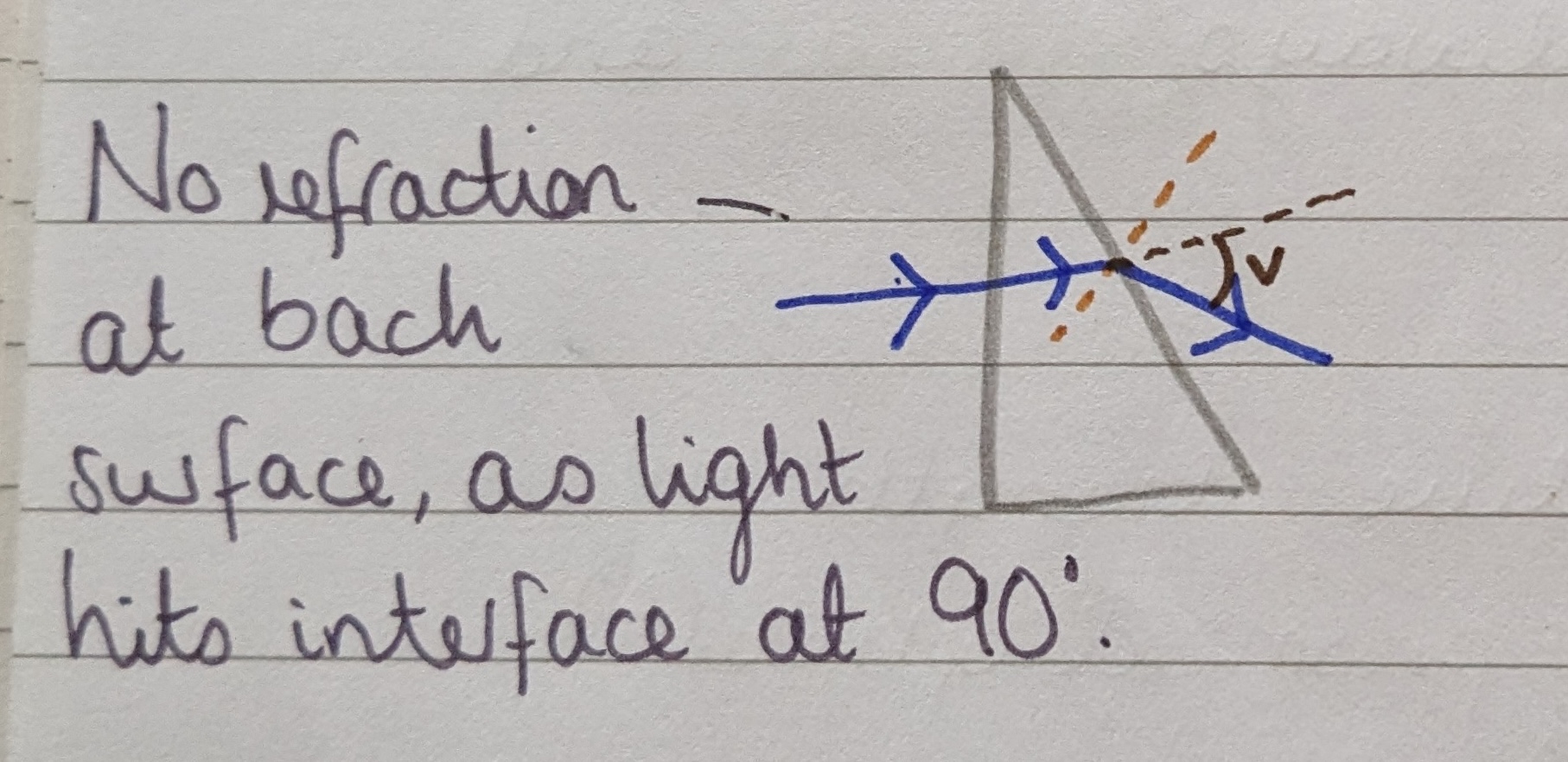
In what position are ophthalmological prisms mounted?

Prentice position, which is the most powerful.

This is because the prisms used in clinic have a very small apical angle hence minimal image degradation.

Lens

An optical device used to alter the vergence of light passing through it. In ophthalmics, refraction is considered to occur at the centre of the lens as they are so thin.

What is the formula to calculate the surface power of a lens?

F = n₂ - n₁ / r

Where F = power, measured in dioptres (D)

n₂ and n₁ are the refractive indices

r = radius of curvature, measured in metres (m)

A positive surface power indicates a converging lens, or convex lens.

A negative surface power indicates a diverging lens, or concave lens.

True or false - a plus lens is a concave lens.

False, a plus lens is a convex lens.

True or false - a negative lens is used to correct myopia.

True, a negative lens is a concave lens used to diverge light for myopia correction.

True or false - a toric lens is used to correct hypermetropia?

False, a toric lens is primarily used to correct astigmatism.

What kind of lens is used to correct hypermetropia?

A plus lens, which is a convex lens, is used to correct hypermetropia by converging light rays.

Calculate the power of a lens, where n₁ = 1.0, n₂ = 1.5, and r = 50cm

Step 1) Plug the values from the question into the power formula:

F = n₂ - n₁ / r

F = 1.5 - 1.0 / 0.5

Step 2) Solve for F:

F = +1.00D

Therefore this is a convex lens with a power of 1.00 dioptre.

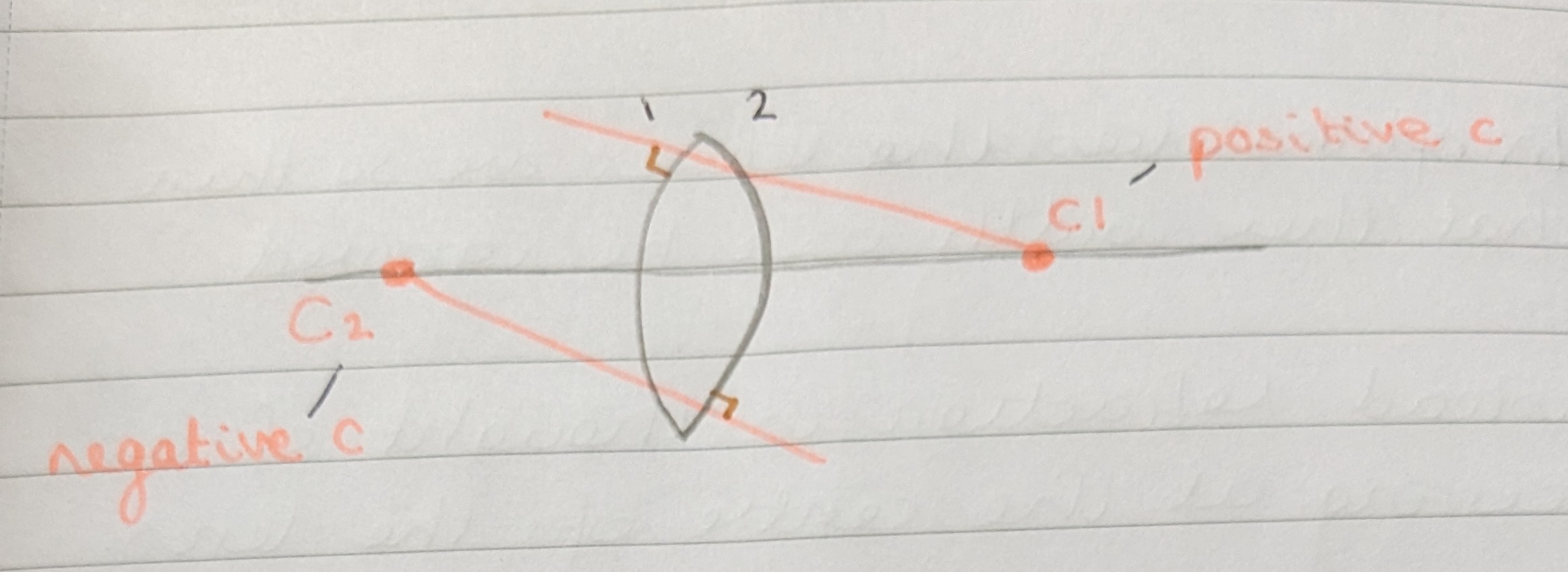
Convex lens

A convex lens, AKA converging or plus lens, is used to correct hypermetropia.

It has two centres of curvature, with c₁ forming behind the lens and c₂ forming in front of the lens.

It will demonstrate image magnification and an against movement.

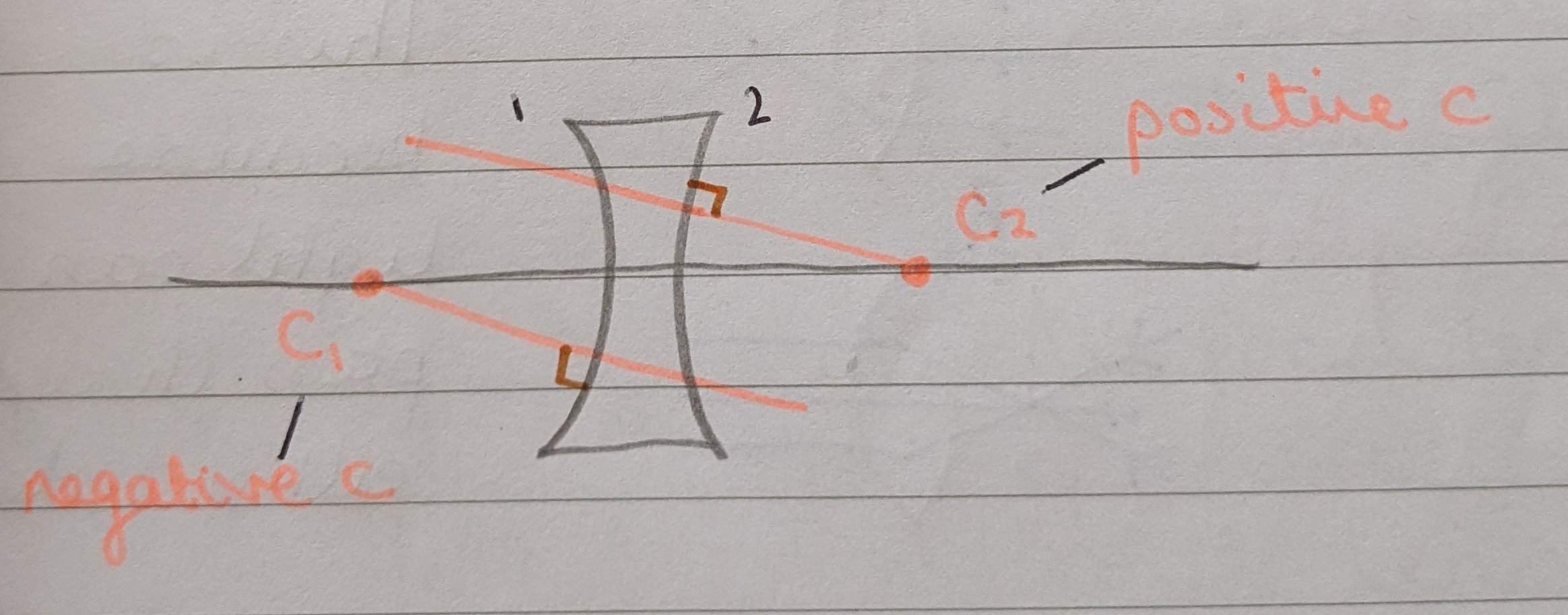
Concave lens

A concave lens, AKA diverging or minus lens, is used to correct myopia.

It also has two centres of curvature, with c₁ forming this time in front of the lens and c₂ forming behind the lens.

It will demonstrate image minification and a with movement.

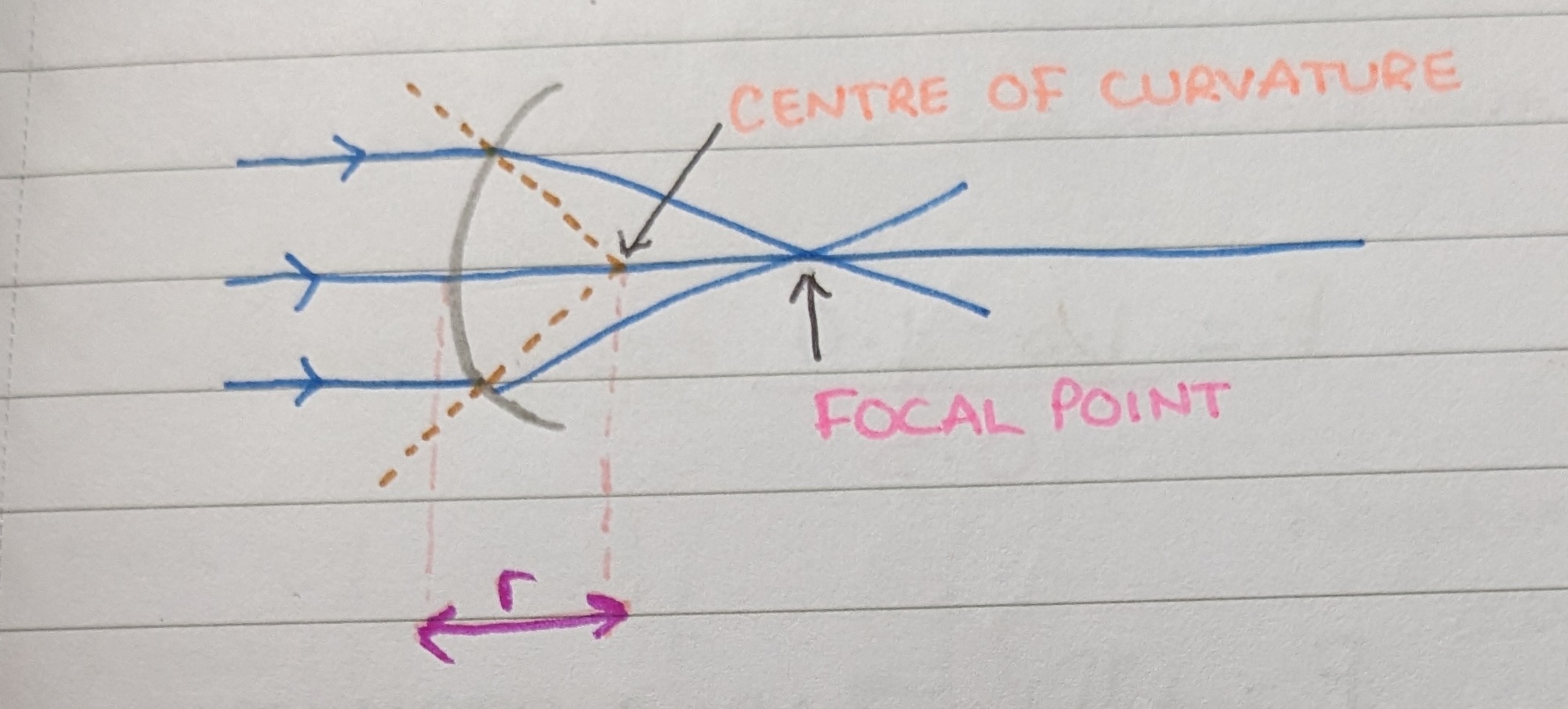
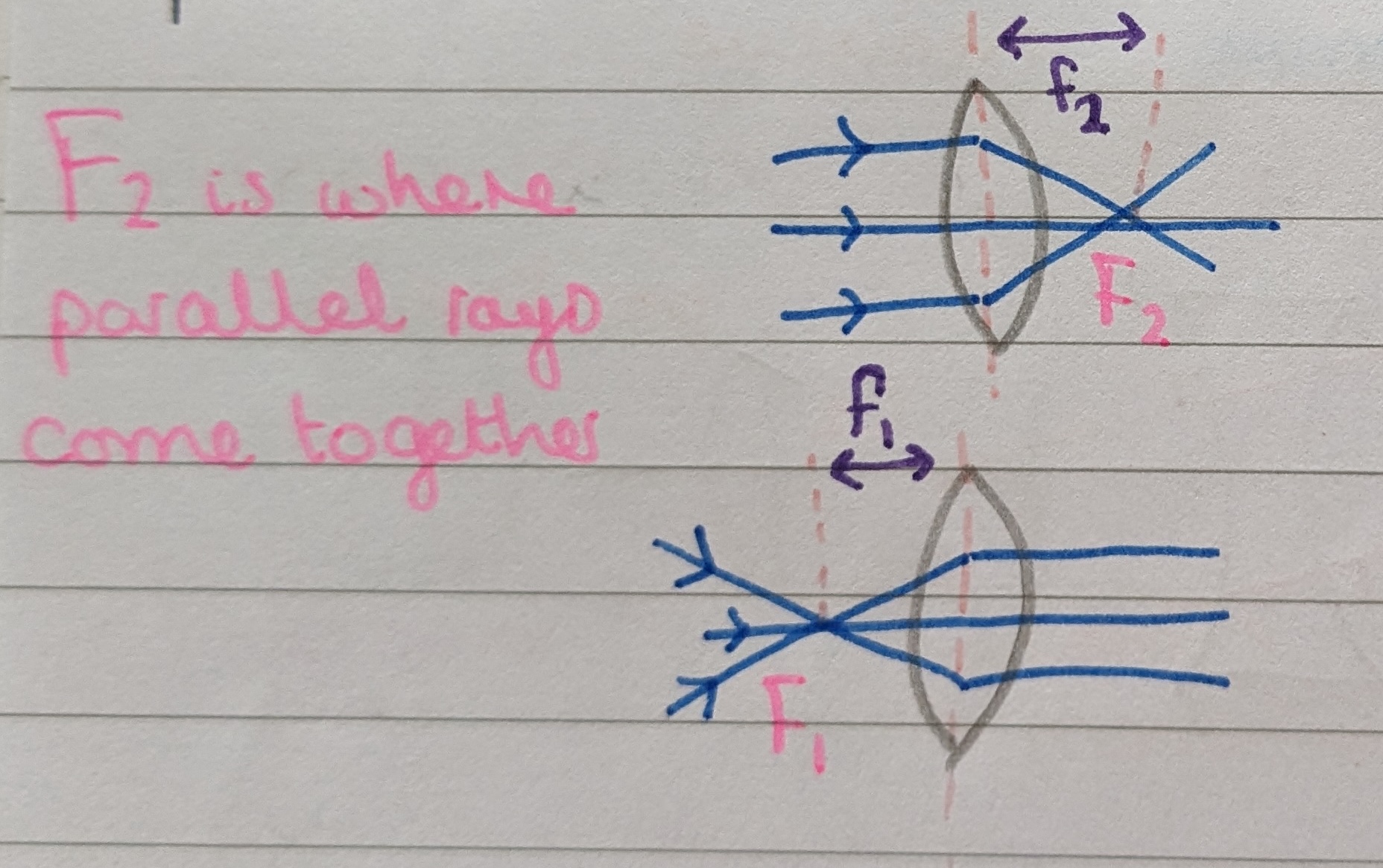
Focal point

A spectacle lens has two focal points, because light can pass through it in either direction. The distance from the focal point to the centre of the lens is the focal length (f), with a shorter focal length indicating a more powerful lens.

F = 1/f₂

or f = 1/F

A focal point which forms in front of the lens is a negative value - f₁ for a convex lens and f₂ for a concave lens.

A focal point which forms behind the lens is a positive value - f₂ for a convex lens and f₁ for a concave lens.

Prentice’s rule

When a lens with power (F) is offset from its centre by d (cm), it causes the same bending of light as a prism.

P = F x d

P = prism power, ^

F = lens power, D

d = distance from the optical centre, cm

Ray tracing

Ray tracing diagrams can be drawn to calculate the size and position of an image formed by a lens. This can also be done mathematically using the equations:

1/f₂ = 1/v - 1/u - Image position

Where f₂ = focal length of the lens, v = image distance, and u = object distance.

m = image size/object size = v/u - Image size

Where m = magnification, v = image distance, and u = object distance.

Calculate the image position if an object measuring 12cm is placed 33cm in front of a +5.00D convex lens.

Step 1) Calculate f₂ using the formula f₂ = 1/F

f₂ = 1/5

f₂ = 0.2m

Step 2) Plug in the values from the question to the image position formula

1/f₂ = 1/v - 1/u

1/0.2 = 1/v - 1/-0.33

Step 3) Rearrange the formula

1/v = 1/f₂ + 1/u

1/v = 1/0.2 + 1/-0.33

1/v = 2

Step 4) Solve for v

v = ½ = 0.5m

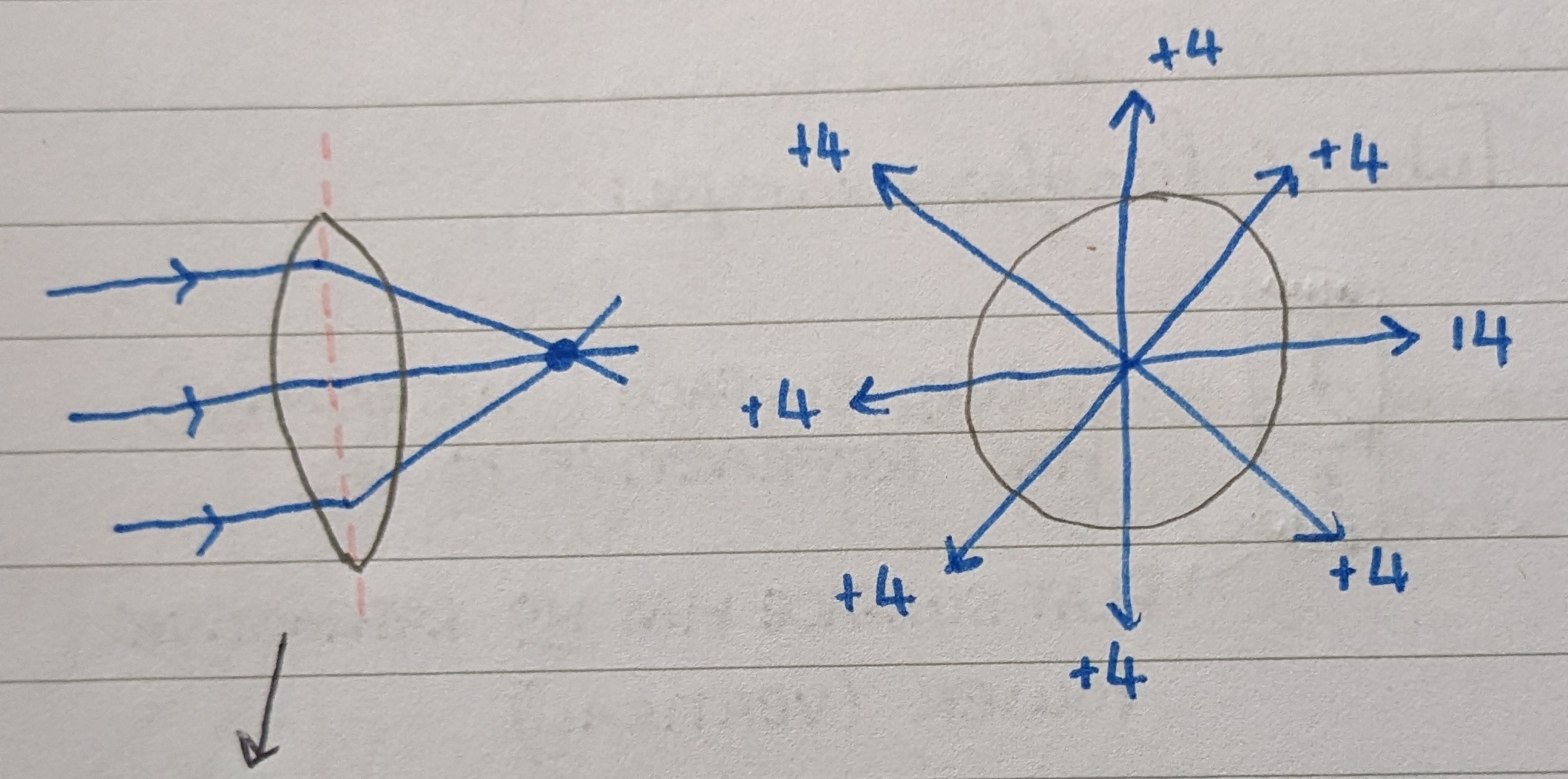
Spherical lens

A lens in which all meridians have the same refractive power, producing a point image. Spherical lenses can be identified as causing image magnification or minification, but no distortion.

Cylindrical lens

A lens that has one principle meridian of zero refractive power, and the other principle meridian with a different refractive power. Cylindrical lenses cause light to converge at different points depending on where it hits the lens, forming a line image. They can be identified as their edges change width going around the edge, and they will cause image distortion until the 0 meridian is hit.

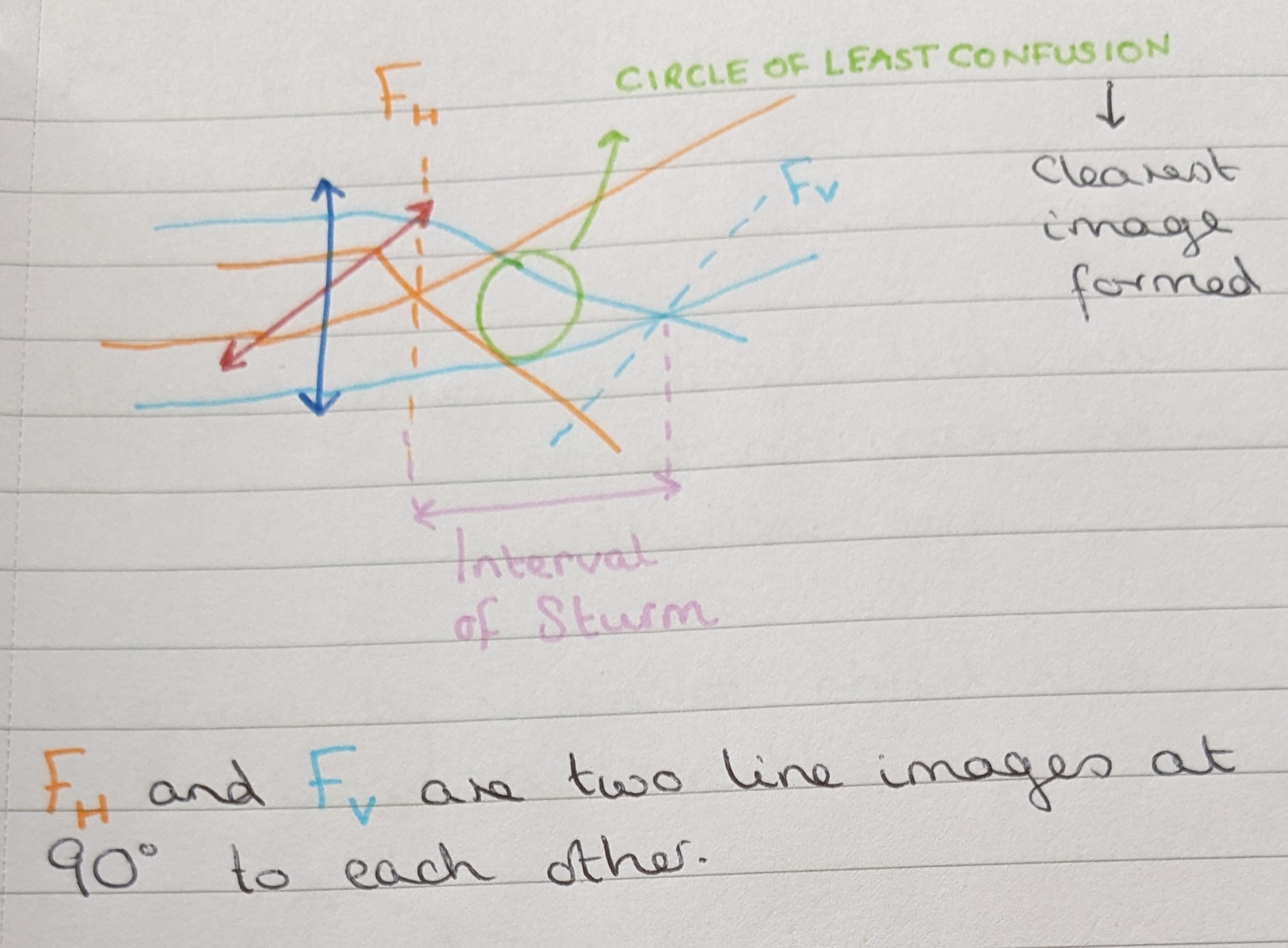
Toric lens

In a toric lens, the two principle meridians each have their own refractive power owing to their different curvatures. They form two line images at 90^o to each other, with the clearest image formed in the circle of least confusion. They can be identified by causing image movement in both meridians, as well as a unique “scissoring” distortion of line images.