AP Stats: The General Addition Rule

Consider this event: In a standard deck of 52 cards, let’s consider three separate events…

Event #1: Jack (J) cards!!!

P(J) = 4/52 (4 jacks in a deck of cards)

Event #2: Red Ace (RA)

P(RA) = 2/52 (2 red ace in a deck of cards)

Event #3: Jack or Red Ace (J or RA)

P(J or RA) = 4 jack+ 2 red ace= 6/52

add the probabilities together

Lets try this again, but with slightly different events…

Event #1: Spade (S)

P(S) = 13/52

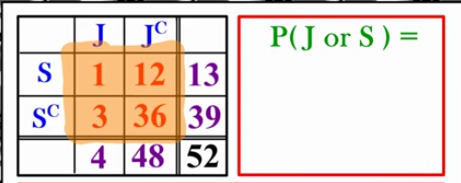
Event #2: Jack or Spade (J or S)

4 Jacks and 13 Spades

There’s a difference here, BUT there’s a piece of the puzzle we’ve left out

P(J) + P(S) - P(J and S ) = P( J or S)

4/52 + 13/52 - 1/52 = 16/52

jack of spades are in both sets of Jacks and Spades! (Repeat value)

Subtract the value that was counted twice

Back to the original example!

P(J) + P(RA) - P(J and RA) = P(J or RA)

4/52 + 2/52 - 0/52 = 6/52

We don’t have to subtract anything because there’s no repeat values in these sets

General Addition Rule

P(A or B) = P(A) + P(B) - P(A and B)

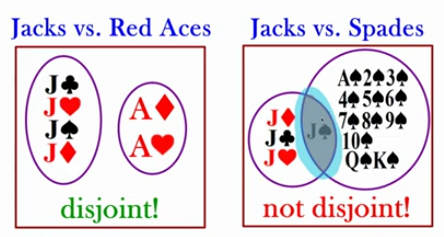
Disjoint vs Not disjoint

If two (or more) events have nothing in common, then the events are called disjoint or mutually exclusive

If two (or more) events have something in common, then the events are not disjoint and not mutually exclusive.

Going back to that general addition rule…

P(A or B) = P(A) + P(B) - P(A and B) = 0 if the events “A” and B” are disjoint

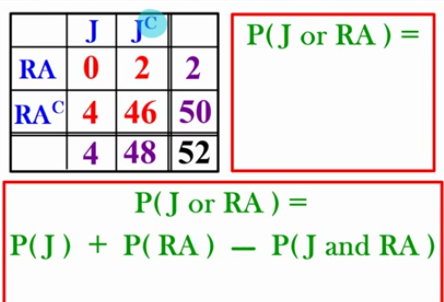
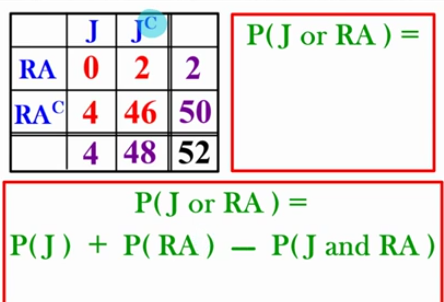
Two Way table Comparisons!

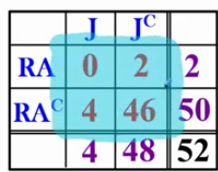
The little C represents any other card that’s not Jacks or Red Aces

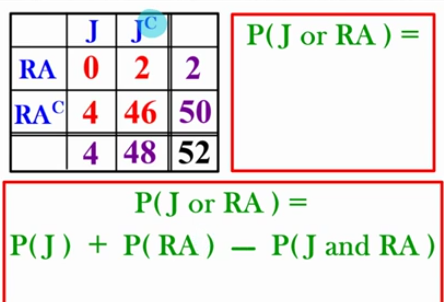
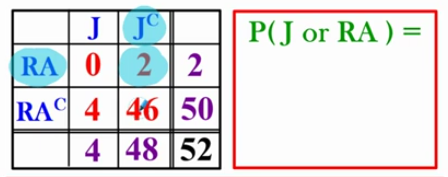
Purple numbers

marginal distributions (tie back to Ch 1) (read from left to right, up and down)

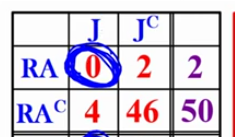
Red numbers

compares both of the subjects;

there are 2 Red aces that are not Jacks

Method 1: Find P(J or RA)

P(J) + P(RA) - P(J and RA)

4/52 + 2/52 - 0/52 =6/52

look at the table

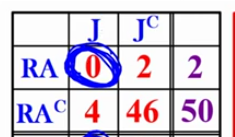
Method 2: Find P(J or RA) without focusing on the marginal distributions

Look at the values’…

Do the values’ on the table represent getting either a Jack or a Red Ace??

0 = yes! represents 0 jacks and 0 red ace

2 = Yes! represents getting 2 red ace

4 = yes! represents getting 4 jacks

46 = no… represents getting cards that are not jacks and not red aces

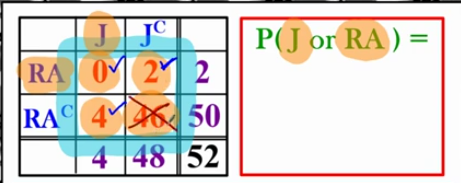
Method 2: P( J or RA)

4 + 2 + 0 = 6/52

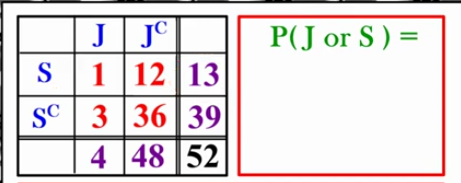
Another example! P(J or S), Using method 1

P(J) + P(S) - P(J and S)

4/52 + 13/5 - 1/52 = 16/52

→ the 1 is counted twice in both jacks and spades

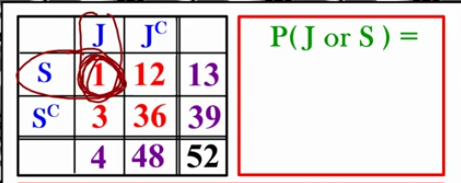
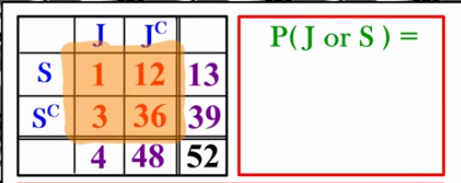
P(J or S) using method 2

P(J or S) = IGNORE THE MARGINS!!!

P(J) + P(S) - P(J and S) =

Do the values’ on the table represent getting either a Jack or a Spade??

1 = yes! (both jack and spade)

12 = yes, represents a spade (not a jack but its ok)

3 = yes, represents a jack (not a spade but still counts)

36 = no, doesn’t represent neither jack or spade

1 + 3 + 2 = 16/52