Discrete Math Exam 3

What is an inverse relation?

R is a relation from A to B. Inverse relation R^-1= {(y, x)∈B x A| (x,y)∈R}

For all x∈A and y∈B, (y,x) ∈ R^-1 if and only if (x,y)∈R

Switch x and y in the ordered pairs of R.

Why is the “divides” relation from A to B for every ordered pair (x, y) ∈ A x B?

x R y if and only if x|y, x divides y, y is divisible by x

What is a relation on a set A?

A relation from A to A

What is a directed graph?

When relation R is defined on a set A, the arrow diagram of the relation can be modified. Instead of representing A as two separate sets of points, represent A only once and draw an arrow from each point of A to each related point. 

N-ary relation

A subset of a Cartesian product of n sets.

2-ary is binary, 3-ary is ternary, 4-ary is quaternary relation.

What is a reflection relation?

For every x∈A, x R x

For every x in A, (x, x) ∈ R

Each element is related to itself

What is a symmetric relation?

for every x, y ∈ A, if x R Y then y R x

For every x and y in A, if (x, y) ∈ R then (y, x) ∈ R

If any one element is related to one element, then second element is related to the first

What is a transitive relation?

For every x, y, z ∈ A, if x R y and y R z then x R z

For every x, y, z in A, if (x,y) ∈ R and (y, z) ∈ R, then (x, z) ∈ R

If any one element is related to a second and the second is related to a third, first and third are related.

Can be vacuously transitive if there are not enough elements in A to prove it.

How to prove a relation is reflexive, symmetric, or transitive?

Write what needs to be proved in terms of x, y, A, and R. Then use the definitions of A and R to rewrite the statement for your particular case. Either see that the proof is immediately obvious or prove using generalizing from the generic particular.

What does universally false mean?

False for every element of its domain

What is the transitive closure?

Let A be a set and R a relation on A. The transitive closure of R is the relation R^t on A that satisfies:
R^t is transitive

R ⊆ R^t

if S is any other transitive relation that contains R, then R^t ⊆ S.

In order to allow R^t to be transitive (Add ordered pairs)

How to show a relation R on an infinite set A is reflexive?

Suppose x is any element of A and show that x R x

How to show a relation R on an infinite set A is symmetric?

Suppose x and y are any elements of A such that x R y and show that y R x

How to show a relation R on an infinite set A is transitive?

Suppose x, y, z are elements of A such that x R y and y R z. Show that x R z

What is a partition?

A finite or infinite collection of nonempty, mutually disjoint subsets whose union is A.

What is mutually disjoint?

Two or more sets have no elements in common

What is the relation induced by the partition?

For every x, y ∈ A, x R y if and only if there is a subset A_i of the partition such that both x and y are in A_i

Which three properties does a relation induced by a partition of a set satisfy?

Reflexivity, symmetry, and transitivity

What is an equivalence relation?

Let A be a set and R a relation on A. R is an equivalence relation if and only if R is reflexive, symmetric, and transitive.

What is the equivalence class of a?

Denoted [a], called class of a

For each element a in A, it is the set of all elements x in A such that x R a.

[a] = {x ∈ A | x R a}

What is the difference between a relation of a set, the set itself, and the equivalence class for an element of the set?

Relation is the rule for the connection between elements, the set is the collection of elements being considered, and the equivalence class is a subset of the set which has all equivalence related elements.

What does [a]_R mean?

The equivalence class of a for the relation R.

How to find the distinct equivalence classes?

Construct the equivalence class for each element in the domain A of the relation. Look at which have the same elements and remove any duplicates. 

How can you prove a statement of the form “if p then (q or r)”

prove "if (p and not q) then r" or “if (p and not r) then q"

What is the partition induced by an equivalence relation?

If A is a set and R is an equivalence relation on A, then the distinct equivalence classes of R form a partition of A. The union of the equivalence classes is all of A, and the intersection of any two distinct classes is empty.

What is the representative of a class?

Suppose R is an equivalence relation on a set A and S is an equivalence class of R. A representative of the class S is any element a such that [a] = S.

What does it mean for m to be congruent to n modulo d?

m ≡ n (mod d) if and only if d| (m-n)

Let m and n be integers and let d be a positive integer. M is congruent to n modulo d if and only if d| (m-n)

If R is an equivalence relation on a set A, and a and b are elements of A, what are the two things the equivalence classes [a] and [b] can be?

identical ([a]=[b]) or disjoint ([a]∩[b]=∅)

What is the equivalence relation for rational numbers/fractions?

Let A = Z x (Z-{0}) and define a relation R on A that for every (a, b) and (c, d) in A, (a, b) R (c, d) if and only if ad=bc. One equivalence class of R for each ration number.

What is antisymmetric?

Let R be a relation on a set A. R is antisymmetric if and only if for every a and b in A, if a R b and b R a, then a = b. 

What is a partial order relation?

A relation that is reflexive, antisymmetric, and transitive. 

What are the two fundamental partial order relations?

Less than or equal to

Subset

What is lexicographic order?

Comparing from left to right to sort sequences (like strings or lists)

How to define a relation ≤?

Let s and t be any strings in S of lengths m and n, respectively, where m and n are positive integers, and let s_m and t_m be the characters in the mth position for s and t respectively.

1. If m≤n and the first m characters of s and t are the same, then s ≤ t.

2. If the first m-1 characters in s and t are the same, s_m R t_m and s_m≠t_m then s≤t

3. If λ is the null string then λ≤ s.
   If no strings are related by ≤ other than by these three conditions, then ≤ is a partial order relation on s

How to make a Hasse diagram?

Start with a directed graph of the relation, placing vertices on the page so that all arrows point upward. Then eliminate the loops at all vertices, all arrows whose existence is implied by the transitive property, and the direction indicators on the arrows

What does it mean for two things to be comparable and noncomparable?

Suppose ≤ is a partial order relation on a set A. Elements a and b of A are said to be comparable if and only if either a≤b or b≤a. Otherwise, a and b are noncomparable.

What is a total order relation?

When all the elements of a partial order relation are comparable.

What is a partially ordered set?

Called poset, set A is a poset with respect to a relation ≤ if and only if ≤ is a partial order relation on A.

Any subset of a partially ordered set is partially ordered.

What is a totally ordered set?

Set A is a totally ordered set with respect to a relation ≤ if and only if A is partially ordered with respect to ≤ and ≤ is a total order.

What is a chain and its length?

Let A be a set that is partially ordered with respect to a relation ≤. A subset B of A is called a chain if and only if the elements in each pair of elements in B are comparable

a≤b or b≤a for every a and b in B. Then length of a chain is one less than the number of elements in the chain.

What is a maximal element

An element in a partially ordered set that is greater than or equal to every element to which it is comparable (might be elements to which it is not comparable). Can have multiple maximal elements. 

What is a greatest element

An element in a partially ordered set that is greater than or equal to every element in the set (so comparable to all elements in set). It is also a maximal. Every finite subset of a totally ordered set has only one. 

What is a minimal element?

An element in a partially ordered set if for each b in A, either a ≤ b or a and b are not comparable. Can be multiple minimal elements

What is a least element?

An element in a partially ordered set that for all elements in the set a≤b (all are comparable). Is also a minimal element. Every finite subset of a totally ordered set has one, but only one.

What does it mean for something to be compatible?

Given partial order relations ≤, ≤’ on a set A, ≤’ is compatible with ≤ if and only if for every a and b in A, if a≤b then a≤’b.

What is topological sorting?

Given partial order relations ≤and ≤’ on a set A, ≤’ is a topological sorting for ≤ if and only if ≤’ is a total order that is compatible with ≤

How to create a total order for a partially ordered set?

Pick any minimal element and make it number one. Then look at set obtained when this element is removed. Since the new set is a subset of a partially ordered set, it is partially ordered. If it is empty, stop the process. If not, pick a minimal element from it and call that element number two. Then look at set obtained when this element is also removed. If set is empty, stop, if not pick a minimal element and call it number 3. Continue until all elements are used up. Put the minimal elements you picked in order, like element 1 ≤ element 2 ≤ element 3

What does it mean for a process to be random?

When it takes place, one outcome from some set of outcomes is sure to occur but it is impossible to predict with certainty which outcome.

What is sample space?

The set of all possible outcomes of a random process or experiment.

What is an event?

A subset of a sample space

What is probability?

If S is a finite sample space in which all outcomes are equally likely and E is an event in S, then the probability of E, denoted P(E) is

the number of outcomes in E/ the total number of outcomes in S

N(E)/N(S)

How to denote the number of elements in A?

N(A)

What is the number of elements in a list?

If m and n are integers and m≤ n, then there are n-m+1 integers from m to n inclusive

m is starting integer and n is ending integer, inclusive

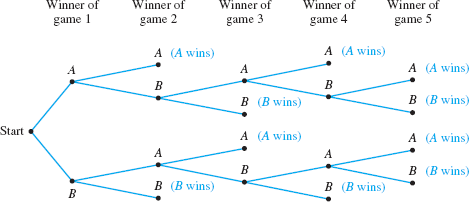
What is a possibility tree?

A way to tell how many possibilities there are

What is the multiplication rule?

If an operation has k steps and the first step is performed in n₁ ways. the second step can be performed in n₂ ways, and then the kth step can be performed in n_k ways, then the entire operation can be performed in n₁, n₂, …, n_k ways

n₁*n₂*n₃*…*n_k

Sometimes doesn’t work if certain paths must be taken, but can reorder which choices happen when to make it work

What is a permutation of a set of objects?

An ordering of the objects in a row

Ex: permutation of set of elements a, b, c is: abc, acb, cba, bac, bca, cab

How many permutations can there be?

For any integer n with 1≤n, the number of permutations of a set with n elements is n!

What is an r-permutation of a set of n elements?

An ordered selection of r elements taken from the set of n elements. The number of r-permutations of a set of n elements is denoted P(n,r). If n and r are integers and 1≤r≤n, then the number of r-permutations of a set of n elements is n!/ (n-r)! n is the number of items in the set, r is the step/ the number of items to be selected and arranged from the set

What does a 4-permutation of a set of seven objects mean?

P(7, 4)= 7!/ (7-4)! = 840

What is the addition rule?

Suppose a finite set A equals the union of k distinct mutually disjoint subsets A₁, A₂, …, A_k. Then N(A) = N(A₁) + N(A₂) + … + N(A_k)

N(A) = number of elements in A

What is the difference rule?

If A is a finite set and B is a subset of A, then N(A-B)= N(A) - N(B)

What is the formula for the probability of the complement of an event

If S is a finite sample space and A is an event in S, then P(A^c) =1-P(A) where A^c = S-A, the complement of A in S

What is the Inclusion/Exclusion rule for two or three sets?

If A, B, and C are any finite sets, then N(A∪B) = N(A)+N(B) - N(A∩B)

and N(A∪B∪C) = N(A) + N(B) + N(C) - N(A∩B)- N(A∩C)-N(B∩C)+N(A∩B∩C)

What is the Pigeonhole Principle?

A function from one finite set to a smaller finite set cannot be one-to-one: There must be at least two elements in the domain that have the same image in the co-domain. 

If there are 6 pigeons and 5 holes, and all are in a hole, then there must be two pigeons in one hole

Generalized Pigeonhole principle

For any function f from a finite set X with n elements to a finite set Y with m elements and for any positive integer k, if km<n, then there is some y∈Y such that y is the image of at least k+1 distinct elements of X. 

What is the contrapositive of the generalized pigeonhole principle?

For any function f from a finite set X with n elements to a finite set Y with m elements and for any positive integer k, if for each y∈Y, f^-1(y) has at most k elements, then X has at most km elements; AKA n≤km

What does it mean for a set to be finite?

It is the empty set or there is one-to-one correspondence from {1, 2, …, n} to it (each item has a partner with no leftovers)

What is the relationship between one-to-one and onto for finite sets?

Let X and Y be finite sets with the same number of elements (AKA X=Y) and suppose f is a function from X to Y. Then f is one-to-one if, and only if, f is onto. And an onto function from a finite set to itself is one-to-one. Such functions are permutations of the sets on which they are defined.

What is r-combination?

Let n and r be nonnegative integers with r≤n. An r-combination of a set of n elements is a subset of r of the n elements.

(n r) n on top r on bottom is n choose r, denotes the number of subsets of size r (or r-combinations) that can be formed from a set of n elements.

AKA C(n, r), nCr, C_n,r or ⁿC_r

Order doesn’t matter. Two unordered selections are the same if they have the same elements, no matter order.

What is an r-permutation?

Order in which they are chosen matters. Two ordered selections are the same if the elements chosen are the same and in the same order. An ordered selection of r elements from a set of n elements.

What is complete enumeration?

Listing all possibilities, good for small n and r values

How to compute r-permutations P(n, r)?

n! / (n-r)! Also, P(n, r) = (n choose r) * r!

How to compute r-combinations? C(n, r)

n! / ( r! (n-r)! )

What is the computational formula for (n choose r)

The number of subsets of size r (or r-combinations) that can be chosen from a set of n elements (n/r) is given by (n choose r) = P(n,r) / r! or also (n choose r) = n! / r!(n-r)! with r≤n.

What does (n choose 0) equal?

1

What does “at least n” mean?

n or more

What does “at most n” mean?

n or fewer

Permutations with Sets of Indistinguishable Objects

Suppose a collection has n objects of which n₁ are of type 1 and are indistinguishable from each other, n₂ are of type 2 and are indistinguishable from each other … n_k are of type k and are indistinguishable from each other. Suppose n₁+n₂+g+n_k= n then the number of distinguishable permutations of the n objects is n!/ n₁!n₂!n₃!…n_k!

When to use multiplication rule and when to use addition rule?

Multiplication rule- If you can imagine the elements to be counted as being obtained through a multistep process in which each step is performed in a fixed number of ways regardless of previous steps

Addition rule- If you can imagine the set of elements to be counted as being broken up into disjoint subsets

How to ensure you’re counting everything and not counting everything twice for multiplication and addition rule?

Multiplication- Does every outcome appear as some branch of the tree? Does any outcome appear on more than one branch of the tree?

Addition rule- Does every outcome appear in some subset of the diagram? Do any two subsets in the diagram share common elements?

What is the formula relating (n choose r) and P(n,r)?

(n choose r) = P(n,r)/r!

What is Pascal’s formula?

(n+1 choose r) = (n choose r-1) + (n choose r) whenever n and r are positive integers with r≤n

What is the binomial theorem?

Given any real numbers a and b and any nonnegative integer n,

(a+b)ⁿ = ∑ⁿ_k=0 (n choose k) a^n-kb^k = aⁿ + (n choose 1) a^n-1b¹ + (n choose 2) a^n-2b² + … + (n choose n-1) a¹b^n-1+bⁿ

What are the nonnegative integer powers of a?

For any real number a and any nonnegative integer n,

aⁿ = { 1 if n= 0 a*a^n-1 if n> 0

What is a binomial coefficient?

If n and r are nonnegative integers and r≤n then (n choose r) is called a binomial coefficient because it is one of the coefficients in the expansion of the binomial expression (a+b)ⁿ

What is closed form?

Without a summation symbol or ellipsis

What does a graph G have?

A nonempty set V(G) of vertices and a set E(G) of edges. Edges are associated with a set consisting of one or two vertices called endpoints. From edges to endpoints is called edge-endpoint function

What is an edge with one endpoint?

A loop

What does it mean for edges to be parallel?

Two or more distinct edges with the same set of endpoints

What does it mean for vertices to be adjacent?

Two vertices connected by an edge. A vertex that is an endpoint of a loop is said to be adjacent to itself

What is incident on and adjacent for edges?

An edge is incident on each of its endpoints, and two edges incident on the same endpoint are called adjacent

What is an isolated vertex?

No edges are incident on it.

Do all edges need vertices and vice versa?

All edges need vertices but vertices do not need edges, isolated vertex.

What is a directed graph/digraph?

Has two finite sets, a nonempty set V(G) of vertices and a set D(G) of directed edges, where each is associated with an ordered pair of vertices called endpoints. If edge e is associated with the pair (v, w) of vertices, then e is the directed edge from v to w.

What is the degree of v?

Let G be a graph and v a vertex of G. deg(v) = the number of edges that are incident on v, with an edge that is a loop counted twice.

What is a walk from v to w?

Let G be a graph, v and w be vertices in G. A walk from v to w is a finite alternating sequence of adjacent vertices and edges of G. Has form v₀e₁v₁e₂…v_n-1e_nv_n where v’s are vertices, e’s are edges, and v₀=1, v_n= w, and for each i=1, 2, … n, v_i-1 and v_i are the endpoints of e_i

What is a trivial walk from v to v?

Has only the single vertex v.

What is a trail from v to w?

A walk from v to w that doesn’t have a repeated edge

What is a path from v to w?

A trail that doesn’t have a repeated vertex

What is a closed walk?

A walk that starts and ends at the same vertex