A.5 Relativity

Reference frame

Set of coordinates to determine different characteristics of objects in that frame

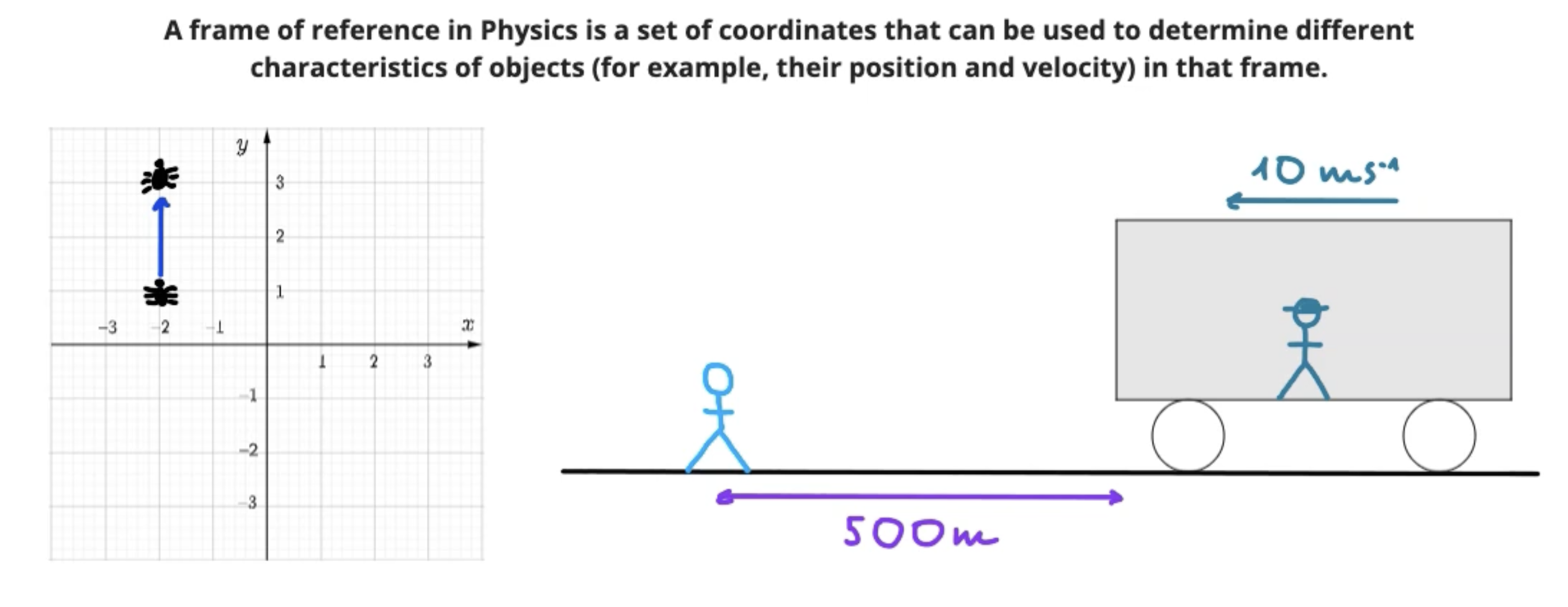
Inertial reference frame

Reference frame that is not accelerated

Either stationary or moving at constant velocity

Newton’s laws hold true in all inertial reference frames

Non-inertial reference frame

Reference frame that is accelerated

Newton’s laws do not hold true in non-inertial reference frames

Galilean relativity

Laws of physics are same in all inertial reference frames

Galilean position transformation equation

x’ = Position in moving reference frame

x = Position in stationary reference frame

v = Velocity of moving reference frame

t = Time in stationary reference frame

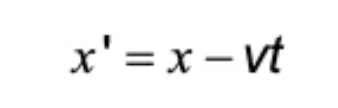
Galilean time transformation equation

t = TIme in moving reference frame

t = Time in stationary reference frame

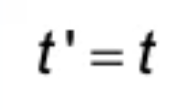
Galilean velocity addition equation

u’ = Velocity in moving reference frame

u = Velocity in stationary reference frame

v = Velocity of moving reference frame

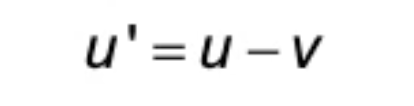
Newton’s first postulate

Space and time are fixed

Time interval between two events same in all reference frames

Newton’s second postulate

Two observers will make the same observations about the world from any inertial reference frame

Einstein’s first postulate

The laws of physics are the same in all reference frames

Einstein’s second postulate

The speed of light in vacuum is the same in all inertial reference frames

Proper time interval

Time measured between two events taking place at the same position in space in the reference frame they occur in

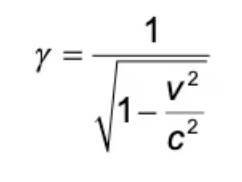
Lorentz factor equation

Gamma = Lorentz factor

v = Velocity of the moving reference frame

c = Speed of light

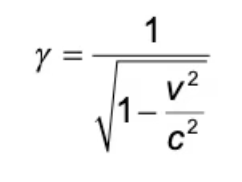
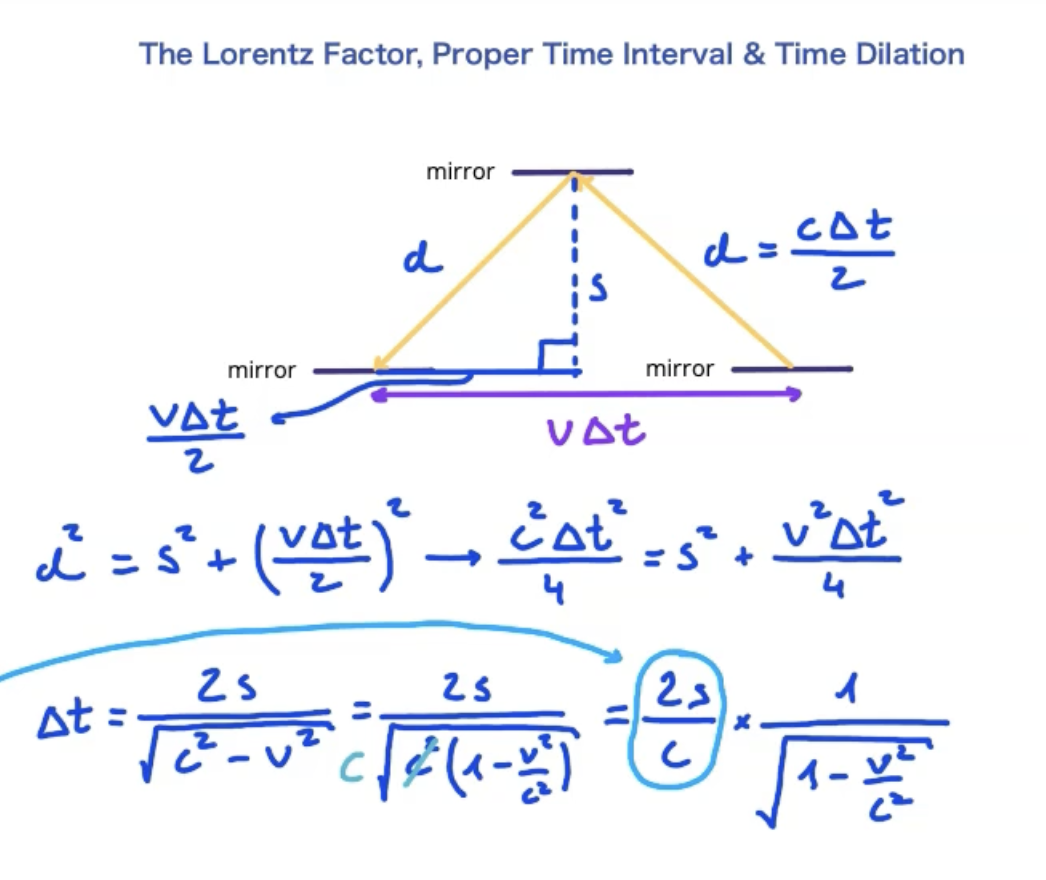
Lorentz factor equation derivation

Draw triangle representing movement of light beam in moving reference frame

Create 2 right-angled triangles

Equate hypotenuses of triangles to speed of light multiplied by time

Lorentz factor

Denotes how much the time interval within a specific reference frame differs from the proper time interval

Used to calculate time dilation using following formula:

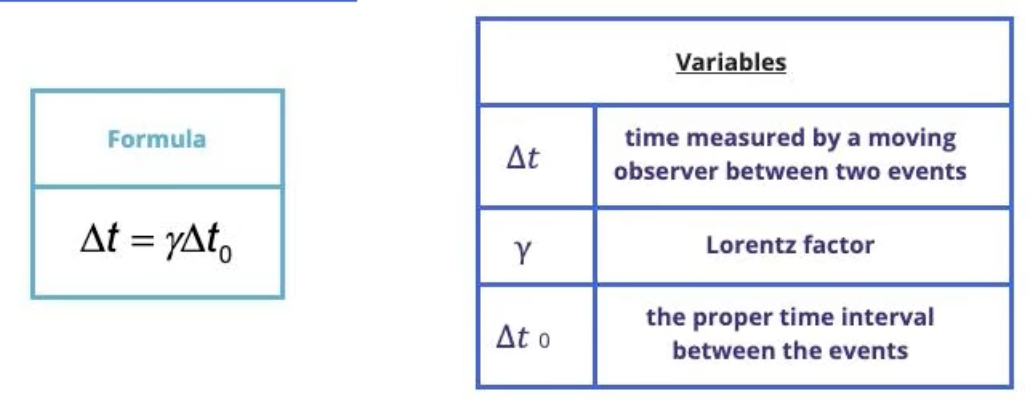
Lorentz position transformation equation

γ = Lorentz factor

x = Position in stationary reference frame

x’ = Position in moving reference frame

v = Velocity of moving reference frame

t = Time in stationary reference frame

Lorentz time transformation equation

γ = Lorentz factor

t’ = Time in moving reference frame

t = Time in stationary reference frame

v = Velocity of moving reference frame

x = Position in stationary reference frame

c = Speed of light

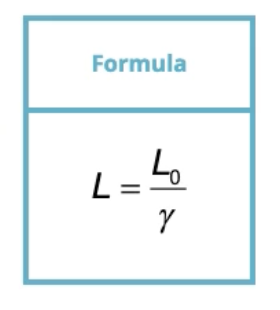
Proper length

Measurement for an object in within a stationary reference frame

Length contraction occurs in reference frame where object is moving

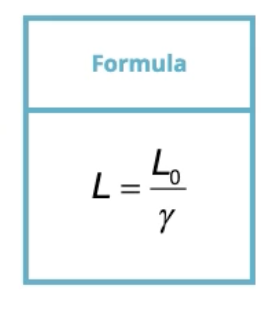
Proper length formula

L = Length in moving reference frame

L₀ = Length in stationary reference frame

γ = Lorentz factor

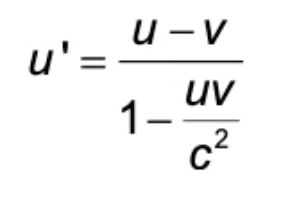
Lorentz velocity addition equation

u’ = Velocity of object in moving reference frame

u = Velocity of object in stationary reference frame

v = Velocity of moving reference frame

c = Speed of light

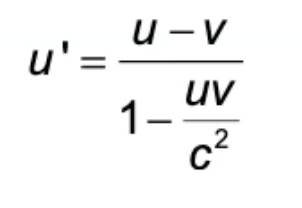
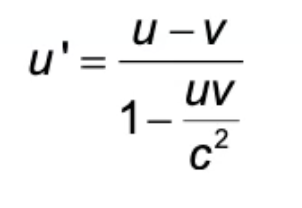
Lorentz velocity addition equation derivation

Write u in terms of x and t and u’ in terms of x’ and t’

Substitute in Lorentz equations for x’ and t’

Substitute in x = ut

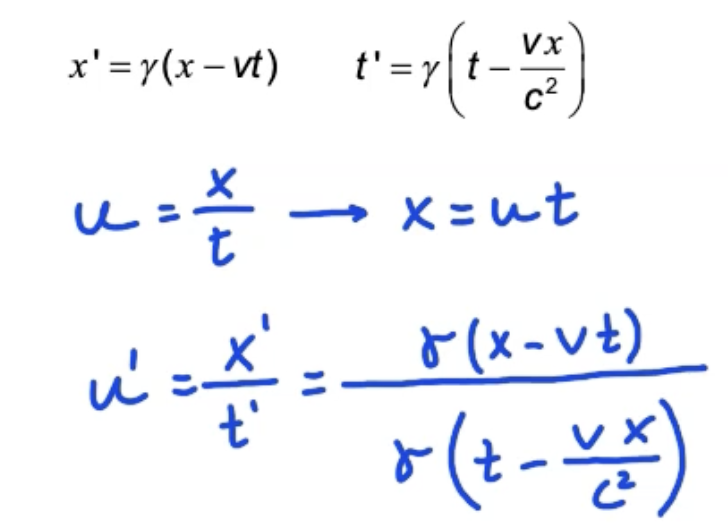
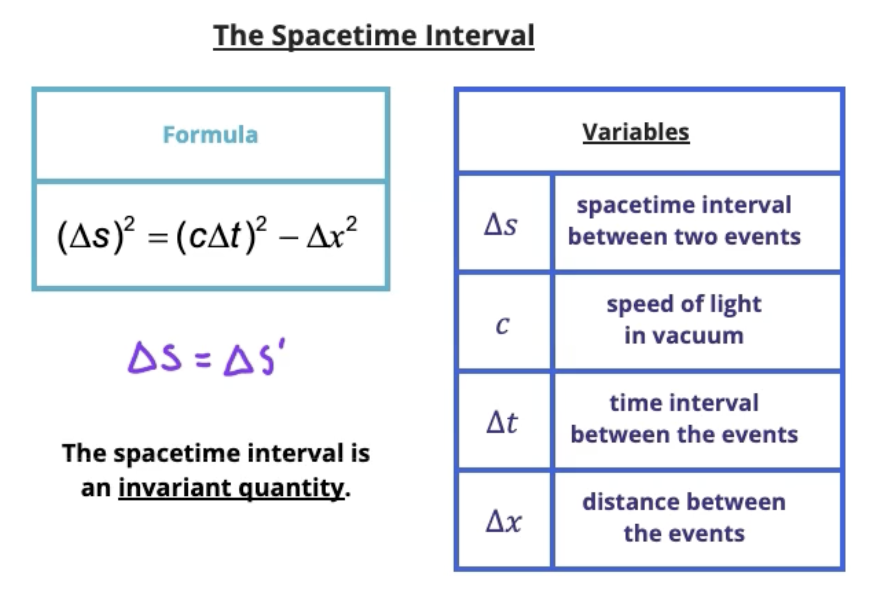
Spacetime interval

Space and time coordinates are not agreed upon between reference frames

Spacetime interval is invariant quantity, agreed upon by observers in all reference frames

Muon decay experiment

Muon mean lifetime is 2.2 × 10^-6 seconds

Muons travel at 0.995c

As they are created around 10km above the Earth’s surface, this means they cannot reach normally (only travel 660m)

However, due to time dilation, their lifetime in the Earth’s reference frame is 2.2 × 10^-5 seconds

This means they can reach the surface, as they travel 6600m

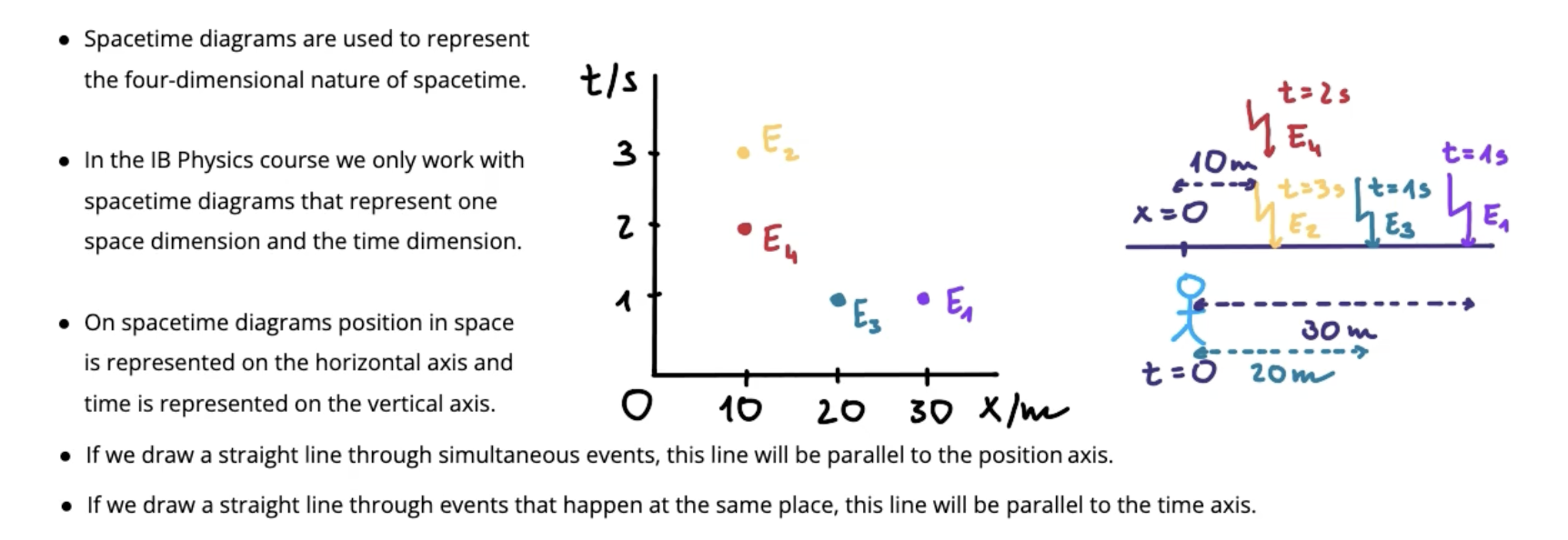
Spacetime diagrams

Represent one space dimension and one time dimension

Draw a line through simultaneous events, parallel to position axis

Draw a line through events at the same place, parallel to time axis

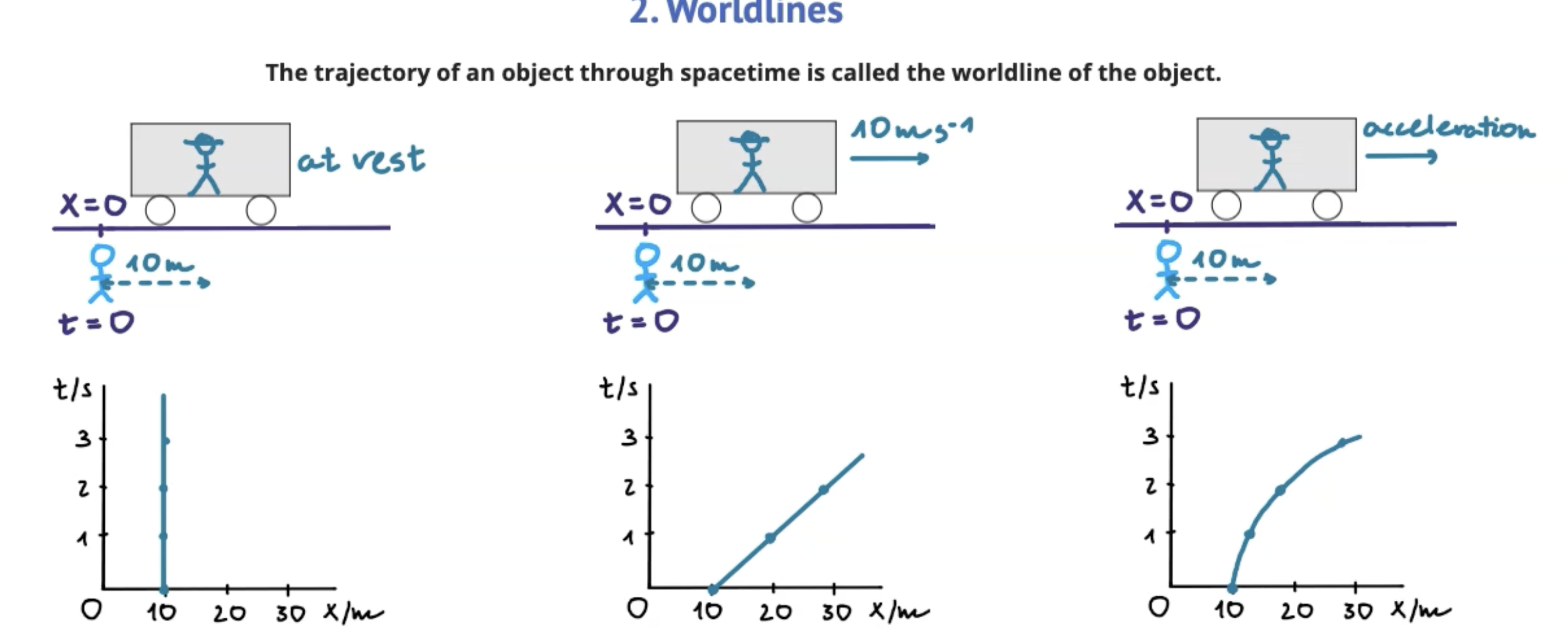
Interpreting spacetime diagrams

Vertical line parallel to time axis means object is at rest

Sloped straight line means object is traveling at constant velocity

Curved line means object is traveling with constant acceleration

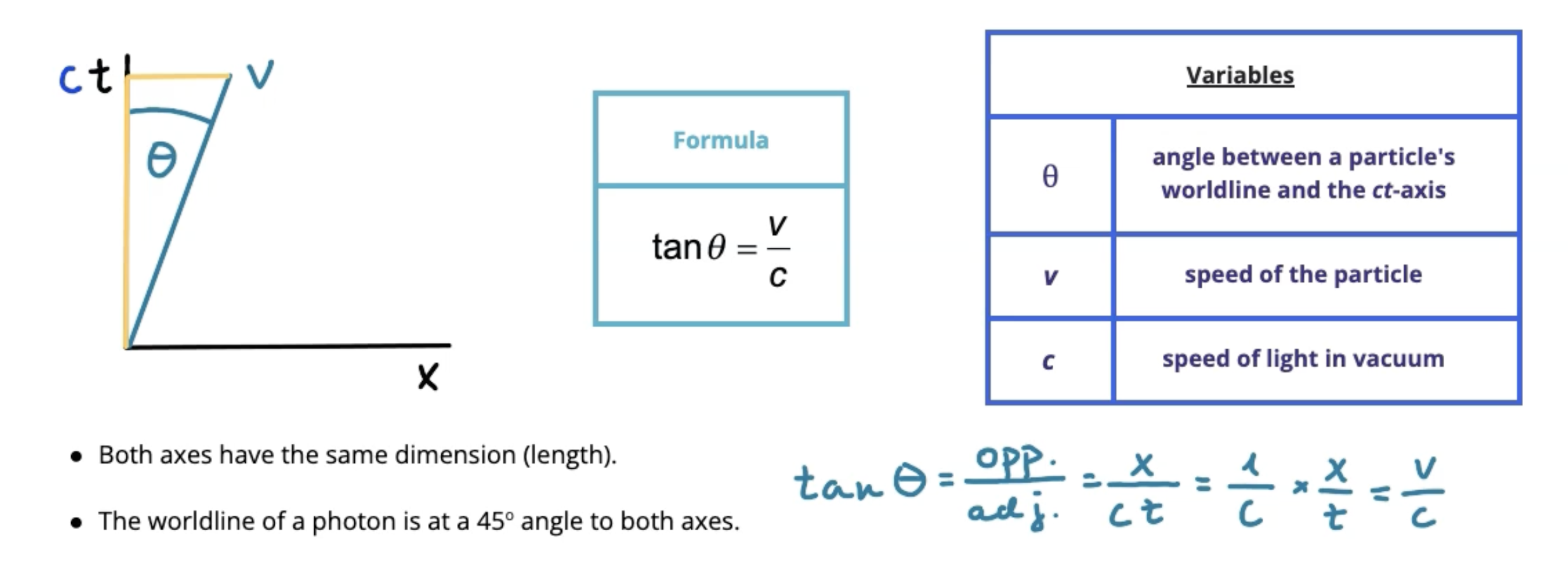
Spacetime diagram formula

Spacetime diagrams often modified with ct on y-axis instead of t

With ct on y-axis, both axes have same dimension (length)

Angle between ct axis and line can never exceed 45 degrees

Angle can be calculated using the following formula

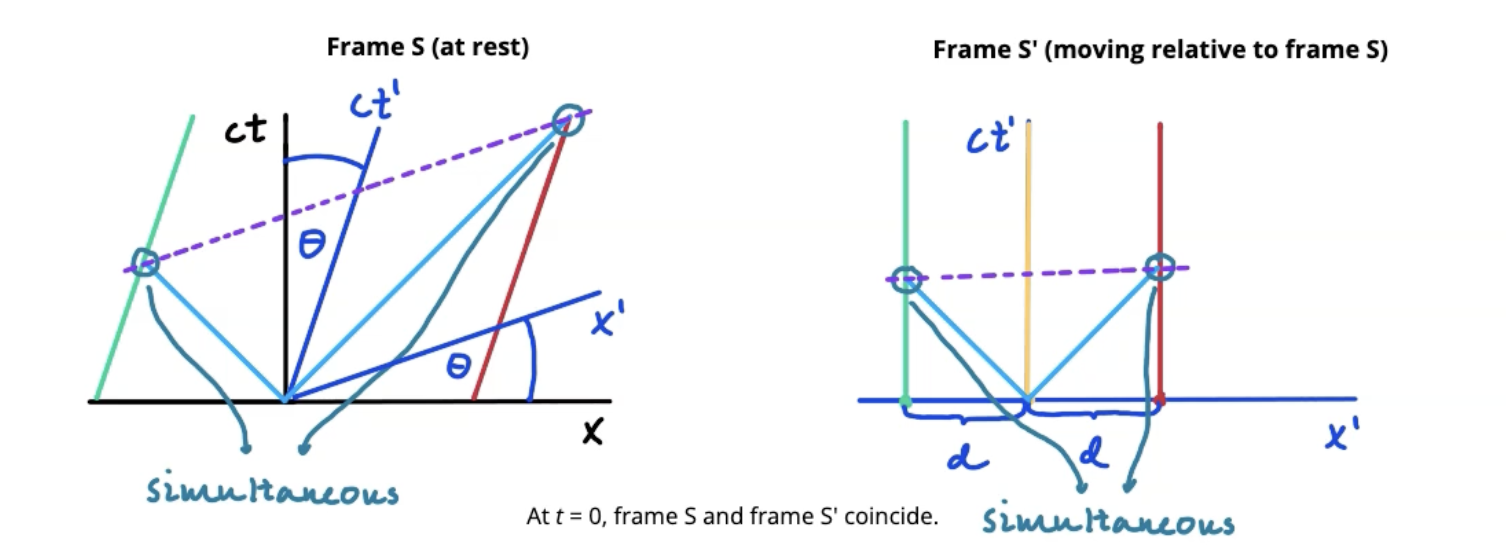
Combining spacetime diagrams

Gaps on stationary RF spacetime diagram are larger than moving RF spacetime diagram due to length contraction

Line representing light is always at 45 degrees

Moving spacetime diagram axis will be at an angle relative to stationary spacetime diagram axis when combined

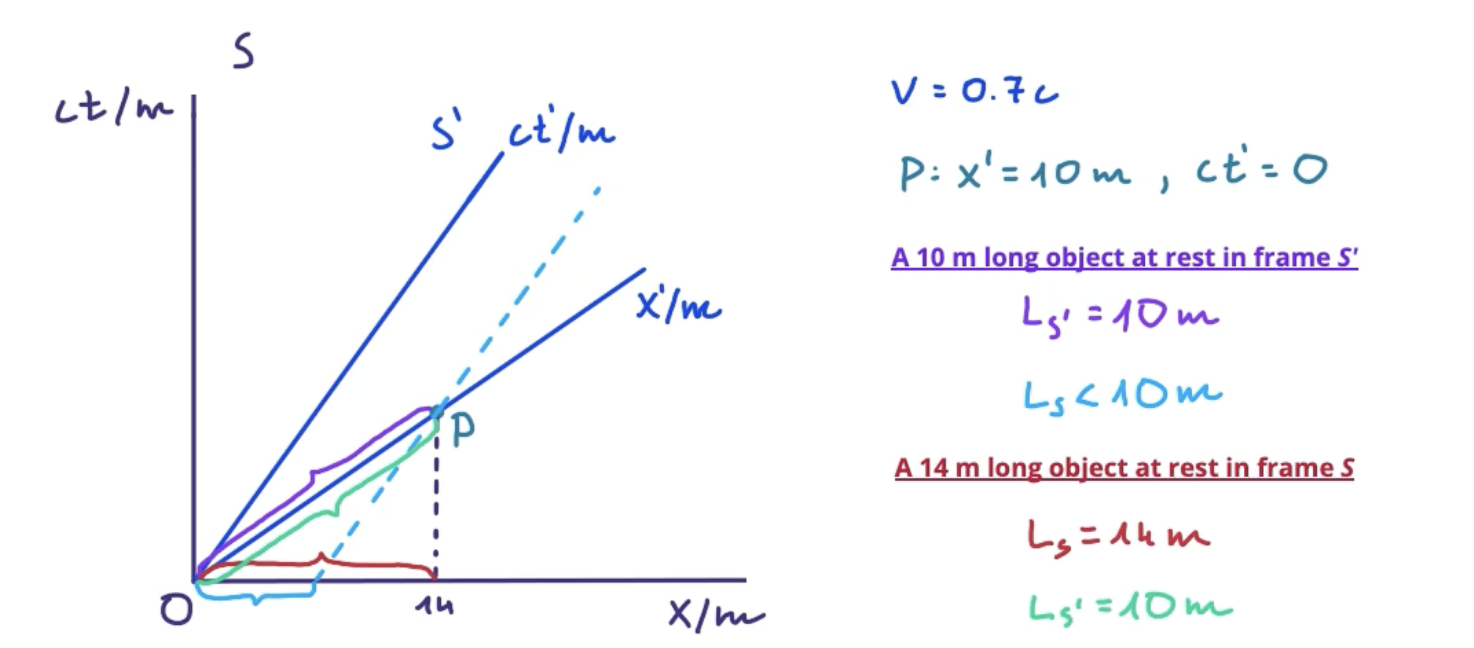
Length contraction on spacetime diagram

Draw parallel line to stationary ct axis connecting it to point on moving distance axis and measure to get scaled value

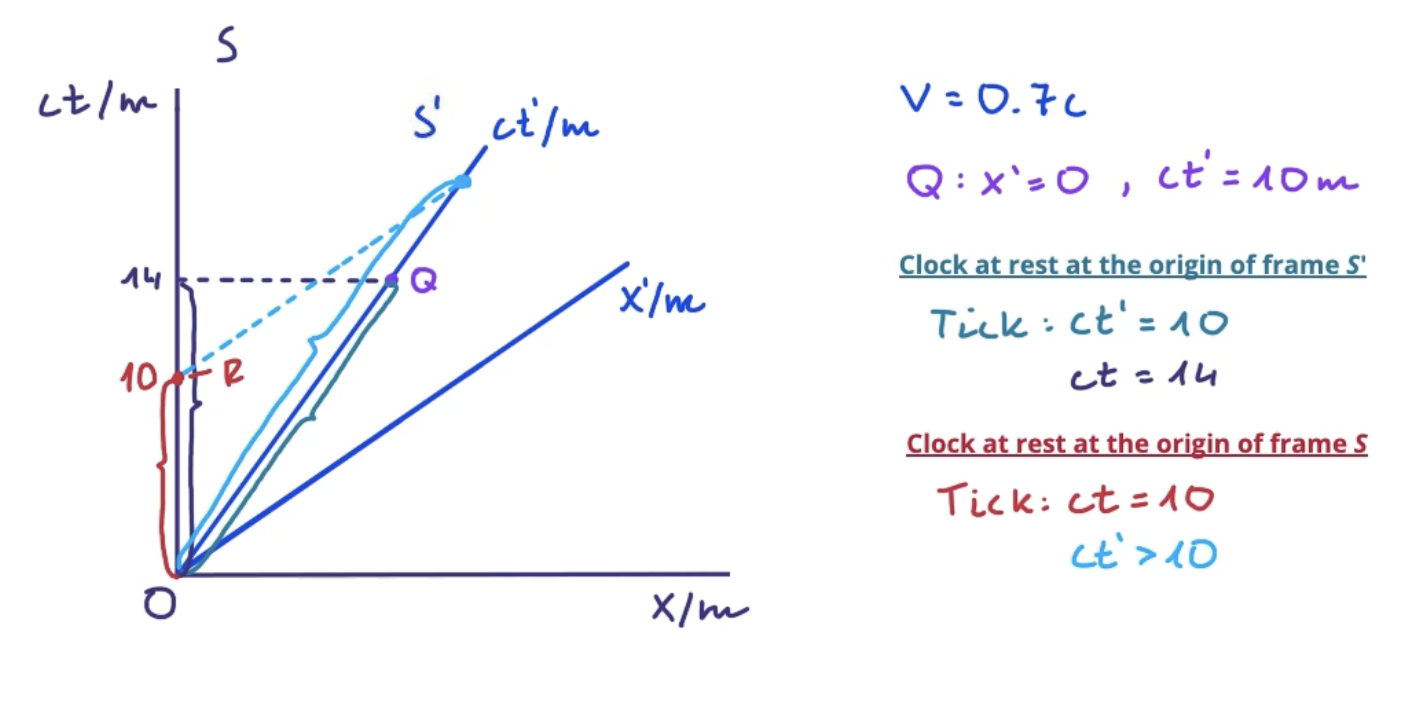
Time dilation on spacetime diagrams

Draw perpendicular line to stationary ct axis connecting it to point on moving ct axis and measure to get scaled stationary time value

Draw parallel line to moving distance axis connecting it to point on moving ct axis and measure to get scaled moving time value

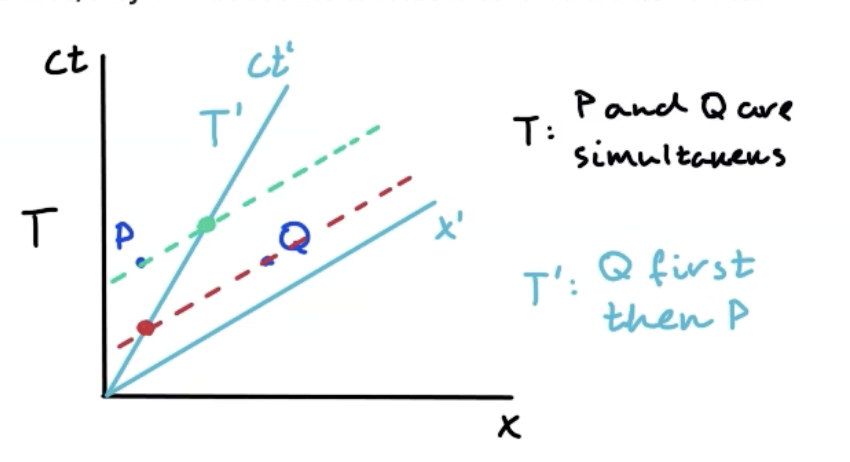
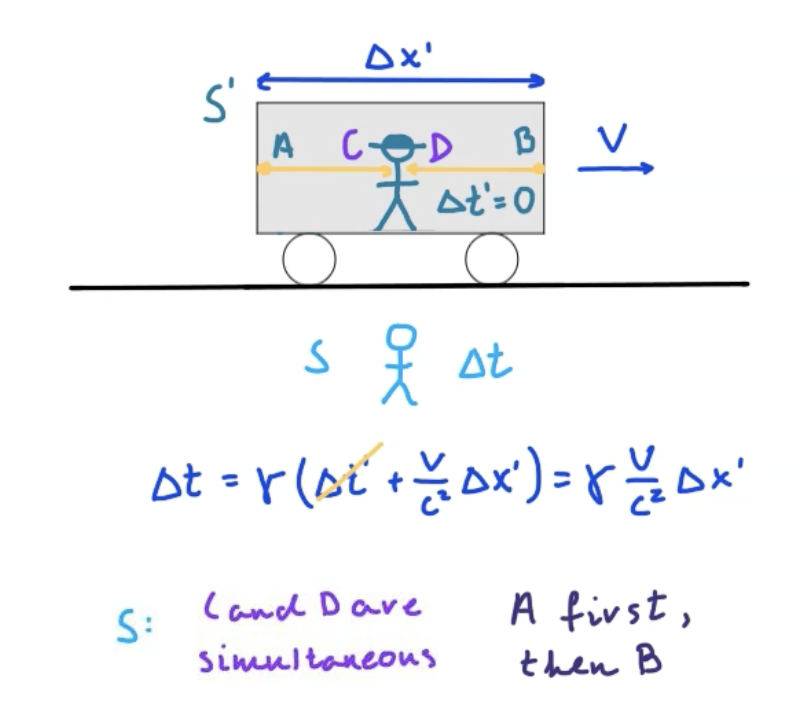
Simultaneity

If Δx between 2 events is 0, then they will be simultaneous in all reference frames

Otherwise, they will not be simultaneous

Event whose light beam reaches first will happen first for stationary observer

How to determine which event happens first in a moving reference frame using a spacetime diagram?

Draw lines parallel to moving distance axis through points representing events

Event whose line intersects the moving ct axis first occurs first