Activity 5: Voltage Variation in a Capacitor

Circuits use ______ to temporarily store energy that can be released as needed.

capacitors

It exists inside a capacitor when energy is stored there

electric field

This increase happens in a curve that follows a mathematical "______" law to its maximum value, after which, the voltage will remain at this "_________" value until there is some other external change to cause a change in voltage

exponential, steady state

From the instant the voltage is applied, the rate of change of the voltage is _____

high

If voltage is applied continuously in a linear manner, the voltage would reach to its maximum value in a time equal to:

5 time constants or 5t

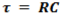
Equation for time constant

r is:

time constant (s)

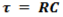
Equation for time constant

C is:

the Capacitance (F)

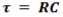
Equation for time constant

R is:

the resistance (ohm)

The voltage across the capacitor, Vc at any instant time during the charging period is given as:

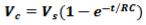
What is the voltage across the capacitor in trial 1 after 47 seconds?

1.926 V

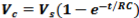
From the graph, approximate VC after 47 seconds in trial 1 and compare it to the computed value using the equation

The voltage is less

Compare the voltage across the capacitor in b to its capacitance when it is fully charged. By how much has it increased?

19.3%

What is the voltage across the capacitor with 100 kΩ in trial 2 after 10 seconds? By how much has it increased?

Use Vc formula. Answer is 6.32V

Vc at any instant time during the discharging period:

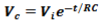
What is the voltage across the capacitor in trial 1 after 47 seconds?

8.07 V

Compare the voltage across the capacitor in a to its initial value when it is fully discharged. By how much has it decreased?

decreased in voltage after t is decreased

In activity 5, how does resistance affect the time to fully discharge in trial 2?

Resistance controls the speed of discharge because it appears in time constant