GCSE Physics- P5 Forces (uncomplete- missing pressure)

scalar

values with a magnitude only

Vectors

values with a magnitude and directioni

scalar examples

speed, temperature, distance, energy

vector examples

velocity, displacement, force, acceleration

displacement

overall distance from A to B in the direction A to B

distance

actual length travelled

acceleration

rate of change of velocity, is a vector

acceleration unit

m/s²

acceleration equation

(v-u)/t or Δv/Δt

v being final velocity or velocity

u being initial velocity

acceleration

if Δv is positive

deceleration

if Δt is negative

velocity

distance per second with a direction

acceleration equation from velocity and displacement

a= (v²-u²)/2s

v being final velocity

u being initial velocity

s being displacement

Distance-time graphs (DT)

gradient of DT graph= speed

velocity-time graphs / speed-time graphs (VT)

gradient of VT graph= acceleration

area of VT graph= distance travelled

Mass

the amount of matter in an object

mass units

Kilograms (Kg)

weight

force on a mass as a result of gravity

weight units

Newtons (N)

Weight equation

W=mg

Free body diagrams

shows forces acting upon an object

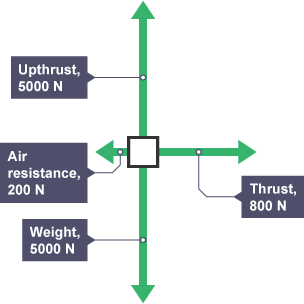
Resultant force

overall force on an object, sum of all the forces acting, accounting for their directions

resultant force equation

F=ma

F being the resultant force

Gravitational field strength unit

N/Kg or m/s²- because acceleration due to gravity

they are equal units

terminal velocity

the maximum speed of which an object falls, there is no more acceleration because the upwards and downwards forces are balanced

Newton’s first law

if the resultant force on an object is zero, the object will stay at rest or continue moving at a constant velocity

ΣF=0 - sum of all forces=0 ∴ acceleration=0

Newton’s second law

resultant force of an object is equal to its mass multiplied by its acceleration

ΣF≠0 - sum of all forces≠0 ∴ acceleration≠0

F=ma

Newton’s third law

when object A exerts a force on object B, object B exerts an equal and opposite force back on object A

always 2 objects with the same line of action

acting on 2 different bodies

Inertia

tendency to do nothing or remain unchanged

inertia mass

measure of how difficult it is to change the velocity of an object, ratio of force over acceleration

inertia mass equation

m= F/a

Momentum equation

P=mv

momentum units

Kilogram metres per second (Kgm/s)

momentum conservation

total momentum before a collision equals the total momentum after a collision

P_before = P_after

Momentum-force equation

F=ΔP/t

F being resultant force

stopping distance

thinking distance + braking distance

thinking distance to speed

proportional

thinking distance factors

tiredness, drugs/alcohol, visibility, tyres/brake conditions, mass passengers and car, speed, age

braking distance factors

speed, brake/tyre condition, road conditions (wet, icy, dry), vehicle+passenger weight

deformation

takes more than one force acting on the same object to cause it do deform (eg. extension, compression, bending), different to action-reaction- both forces act on same object

Hooke’s law practical variables

independent: Force (N)

dependent: extension of spring (cm)

controls: spring constant (N/m), type of spring, position of measurement

Hooke’s law

extension of a spring ‘e’ is directly proportional to the force applied ‘F’

Hooke’s law equation

F=ke

k is the spring constant- force constant/spring constant measuring stiffness of spring

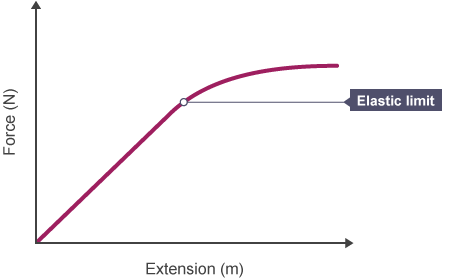
Limits of proportionality / elastic limit

point in which force is not proportional to length

elastic deformation

temporary deformation, bonds between atoms extended, but not broken

plastic deformation

permanent deformation, bonds between atoms broken

Elastic potential energy (E_e)

energy stored in a object caused by a force that deforms elastically, E_e of a spring that obeys Hooke’s law is equal to the work done by the force to stretch (or squash) the spring

Elastic potential energy (E_e) equation

E_e= ½ke²

k being spring constant

e being extension

Work done

energy transferred (J)

Work done equation

W=Fs

W being work done

s being distance moved (in the direction of the force)

work done units

Joules (J)- same as enegy

pivot

the point around which something rotates

Moment

the turning effect of a force- a force that is further from the pivot which depends on size of force and the distance from pivot

Moment equation

M=fd

M being moment

d being distance from pivot

Moments units

Newton-metres (Nm)- 1 Nm is equal to 1 Joule (J)

Lever

rigid bar pivoted on a fixed point (used to transmit force)

Load

force provided by the object you are trying to move

effort

force applied to move the load (work done)

gears

rotating wheel with teeth (cogs) that interlock with another wheel

multiplying force

bigger wheel transmits a smaller force than a smaller wheel, a bigger wheel rotates slower than a smaller wheel