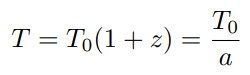Astrophysics Equations

Newtons Law

F = ma

Pressure

ρ = M/V

Volume of a sphere

V = 4/3πr³

Magnitude when m₀ is known

m = -2.5logF + m₀

Magnitude (two stars)

m₁ - m₂ = -2.5logF₁/F₂

Momentum

p = mv

Angular Momentum

L = r x mv

Gravitational Force

F = -GMm/r²

Distance Modulus

m - M = -5 + 5logd (d in parsec)

Centripetal force

F = mv²/r

Photon Energy

E = hf

Photon momentum

p = E/c

Kinetic Energy

E_k = ½mv²

Wien’s Displacement law (estimating the surface temp of a star)

λ_max ∝ 1/T

Potential Energy

E_p = -GMm/r OR mgh

Stefan-Boltzman law (Observational Astrophysics)

F = σT⁴

Escape velocity

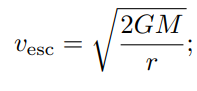
Orbital Velocity

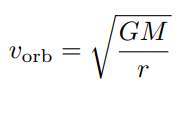
Effective Temperature

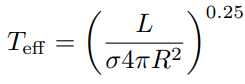
Distance and Parallax

d = 1/p (d in parsec; p in arcsec)

Lens Formula

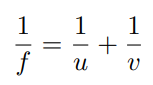
Lens Magnification

M = -v/u

telescope Magnification

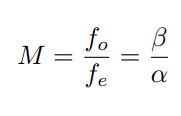
proper motion and velocity (speed of movement of a star in the sky)

v = µ x 4.74 x d (in arcseconds/year)

Flux and Luminosity relationship

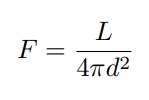
Resolution

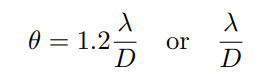
Gravitational potential energy for a star

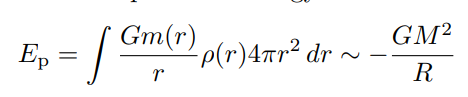
Snells law

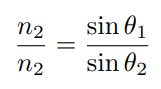
Kelvin_Helmholtz timescale (over which internal energy is radiated away in a star)

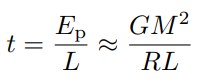
Grating

d sin θ = mλ

Schwarzschild radius

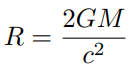
Orbital period (kepler)

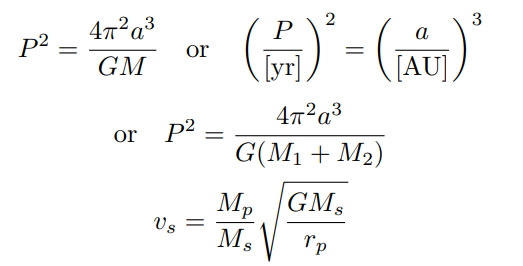
Rotation Curves (galaxies)

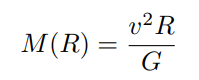
redshift

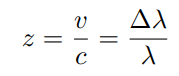
Temperature of a planet

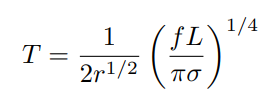
Hubble Law

v = H₀r; H₀ = 70 ± 5 km s^-1Mpc^-1

Hubble Time

t = 1/H₀

Virial Theorem

E_p + 2E_k = 0 or E_p + 2E_th = 0

Critical Density

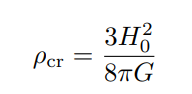
Hydrogen Line Spectrum

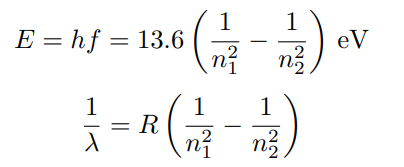
Dynamical Timescale

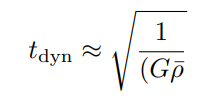
Hydrostatic equilibrium and gravity

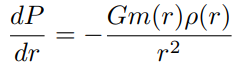
ideal gas law

P = nkT

Thermal Energy

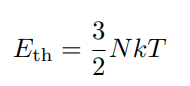
Scale factor

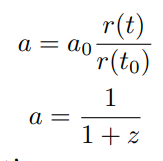
Hubble ‘constant’

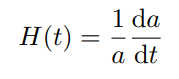
density parameter (relating to hubbles law)

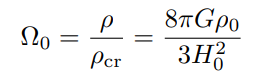
Friedmann equation

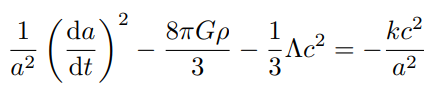
CMB Temperature