SM 143 Deflection of beams

Curvature formula

• 1/ρ is called curvature. EI is called flexural rigidity.

• ρ is radius of curvature, M is internal moment, E is young modulus, I is moment of inertia.

• sign of ρ depends on direction of M: when M is positive, ρ extends above the beam in positive υ direction, and vice versa

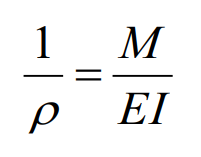
Calculus relationships from w(x) to v

From curvature onwards always have 1/EI

clarification: Integral of M(x) = θ/EI + C

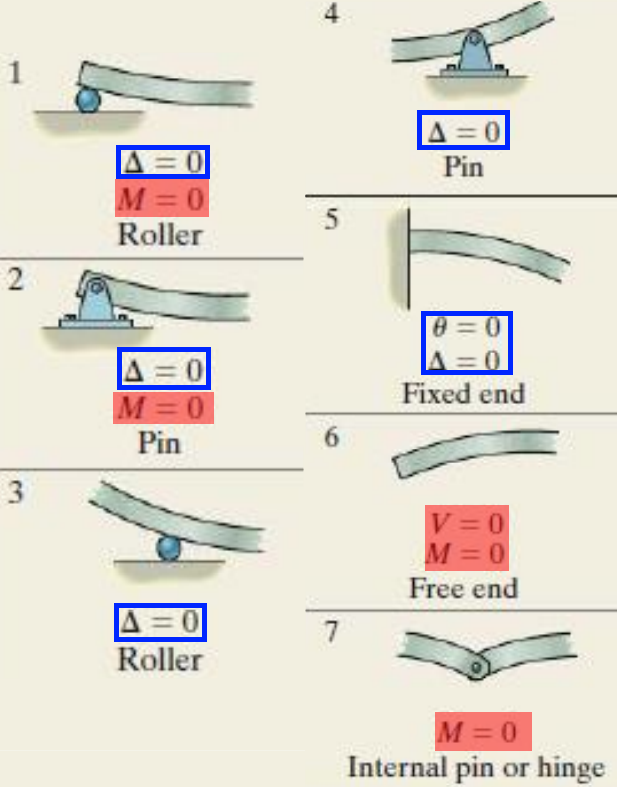
Boundary conditions

• At point force (includes supports) that is not at ends of beam: θ₁ = θ₂, which can be used to equate slope equations to left and right of boundary

Only θ and y is important for slope and deflection formulas

Finding Cs

Use boundary conditions and boundary positions.

eg. x = L/4 is boundary position and at that boundary θ₁ = θ₂. Substitute L/4 into your θ₁ & θ₂ equations to equate some C values.

eg. at x = 0, y₁ = 0, then all x terms get cancelled and C is set to 0.