AP Calculus AB Midterm Exam

General Power Rule

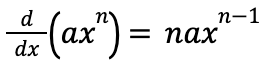
d/dx (sin x)

cos x

d/dx (cos x)

-sin x

d/dx (tan x)

sec²x

d/dx (cot x)

-csc²x

d/dx (sec x)

secxtanx

d/dx (csc x)

-cscxcotx

d/dx (arcsinx)

d/dx (arccosx)

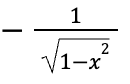
d/dx (arctanx)

d/dx (arccotx)

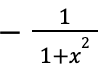
d/dx (arcsecx)

d/dx (arccscx)

d/dx (a^f(x))

(a^f(x))(f’(x))(ln a)

d/dx (e^x)

e^x

d/dx (log_a f(x))

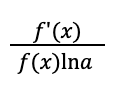
d/dx (ln x)

1/x

Product Rule

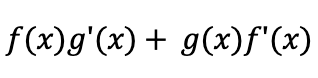
Quotient Rule

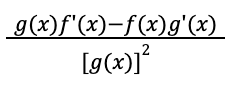
Chain Rule

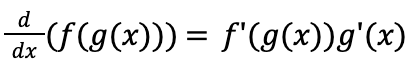
Squeeze Theorem

If g(x)≤f(x)≤h(x) and if g(x) = L and h(x) = L then f(x) = L

Intermediate Value Theorem

If a function f is continuous on a closed interval [a,b], then f takes on every value between f(a) and f(b) on the interval [a,b].

Extreme Value Theorem

If a function is continuous on [a,b], then there is an absolute max and an absolute min on [a,b].

Mean Value Theorem

If a function is continuous and differentiable on [a,b], there is a point c in between a and b such that

Continuity

1. lim f(x)_x→a exists

2. f(a) exists

3. lim f(x)_x→a = f(a)

Average Rate of Change (AROC)

The average range at which a quantity changes over a given interval

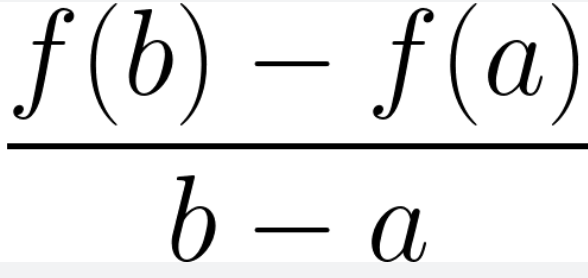
Instantaneous Rate of Change

The exact or precise rate at which a quantity is changing at an instant or specific point

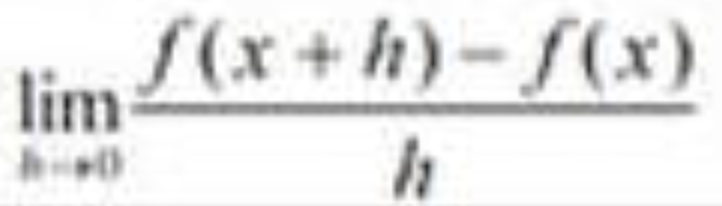
Limit of a Forward Difference Quotient

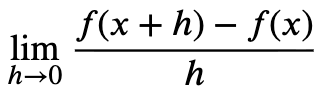
Limit of a Backwards Difference Quotient

Limit of a Symmetric Difference Quotient

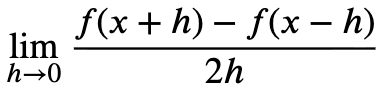
Limit at a Specific Point

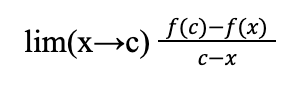
Point-Slope Form

y-y₁ = m(x-x₁)

Normal Slope

Negative reciprocal of the tangent slope

Implicit Differentiation

Write dy/dx next to every y-variable & solve for dy/dx

Position

Original/Given Function

Velocity

f’(x) = rate of change of position (average velocity uses position)

Acceleration

f’’(x) = rate of change of velocity (average acceleration uses velocity)

Average Velocity

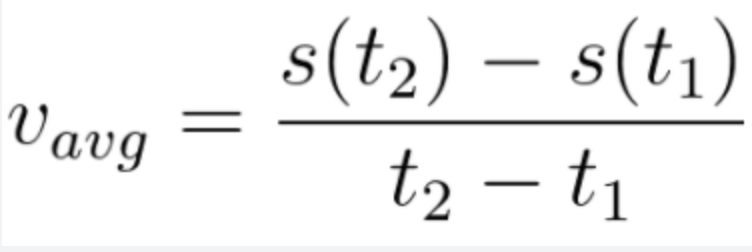
L’Hôpital’s Rule

If lim_x→a f(x)/g(x) yields either of the indeterminate forms 0/0 or ± ∞/∞, then lim_x→a f(x)/g(x) = lim_x→a f’(x)/g’(x)

1/∞

0

e⁰

1

Critical Points

When f’(x) = 0 or f’(x) = DNE

Absolute Maximum

Highest y-value that occurs on a closed function

Absolute Minimum

Lowest y-value that occurs on a closed function

Rolle’s Theorem

If a function is continuous and differentiable on [a,b] and f(a) = f(b) then there exists at least one value, c, in (a,b) such that f’(c) = 0 (AROC = IROC)

Local Minimum

Where f’(x) changes from negative to positive

Local Maximum

Where f’(x) changes from positive to negative

Related Rates

Multiple variables changing at one time and they are related to each other. Always taken in terms of time (dx/dt)

First Derivative Test

1. Take f’(x) and set equal to zero and DNE values to find x-values of critical points

2. Put critical point x-values on a sign chart to find where the slope of f(x) is increasing/decreasing and where the local max/local min are

Second Derivative Test

1. Take f’’(x) and set equal to zero and DNE values

2. Put x-values of f’’(x) on sign chart to find concavity and points of inflection

Point of Inflection

A point where f’’(x) changes sign & halfway between local min and local max

When f’(x) is positive, then f(x) is

Increasing

When f’(x) is negative, then f(x) is

Decreasing

When f’’(x) is positive, then f(x) is

Concave up

When f’’(x) is negative, then f(x) is

Concave down

When f’’(x) is positive, then f’(x) is

Increasing

When f’’(x) is negative, then f’(x) is

Decreasing

When f’(x) is increasing, then f(x) is

Concave Up

When f’(x) is decreasing, then f(x) is

Concave down