LeetCode

DS/Algos

BST propetries

• Left < Root < Right

• Inorder traversal of BST gives a sorted array.

• Duplicates are typically not allowed (depends on implementation).

• Height affects performance — ideally balanced (O(log n)).Each node has at most two children.

LeetCode 108 – Convert Sorted Array to BST
How do you solve it?

Back:

• Goal: Build a height-balanced BST from a sorted (ascending) array.

• Key idea: Middle element becomes the root → ensures balance.

• Steps:

  1. Base case: if array (or subarray) is empty → return None.

  2. Find middle index mid = (l + r) // 2.

  3. Create node TreeNode(nums[mid]).

  4. Recursively build:

     • root.left = helper(l, mid - 1)

     • root.right = helper(mid + 1, r)

  5. Return root.

• Complexity: O(n) time, O(log n) recursion stack.

💡 Dijkstra’s Algorithm
How does it find the shortest paths in a graph?

• Goal: Find the shortest path from a source node to all other nodes in a weighted graph (no negative weights).

• Key idea: Greedy approach — always pick the unvisited node with the smallest tentative distance.

• Steps:

  1. Initialize distances: dist[source] = 0, all others = ∞.

  2. Mark all nodes unvisited; use a priority queue (min-heap) for efficiency.

  3. While unvisited nodes remain:

     • Pick node u with smallest distance.

     • For each neighbor v of u:

       • If dist[u] + weight(u,v) < dist[v], update dist[v].

     • Mark u as visited.

  4. Repeat until all reachable nodes processed.

• Complexity:

  • O(V²) with simple array

  • O((V+E) log V) with min-heap / priority queue

• Tips:

  • Works only with non-negative weights.

  • Similar patterns appear in shortest-path problems (graphs, grids, maps).

  • Can track paths using a parent map.

💡 Bellman-Ford Algorithm
How does it find shortest paths in a graph?

• Goal: Find shortest paths from a source node to all other nodes in a weighted graph, including negative weights.

• Key idea: Dynamic programming — relax all edges repeatedly.

• Steps:

  1. Initialize distances: dist[source] = 0, all others = ∞.

  2. Repeat V-1 times (V = number of vertices):

     • For each edge (u, v) with weight w:

       • If dist[u] + w < dist[v], update dist[v] = dist[u] + w.

  3. Optional: Check for negative cycles by relaxing all edges once more.

     • If any distance improves → negative cycle exists.

• Complexity: O(V × E)

• Tips:

  • Can handle negative weights (unlike Dijkstra).

  • Useful in graphs where edges may reduce total cost.

  • Keeps track of paths using a parent array.

💡 LeetCode 76 – Minimum Window Substring
Task: Find the smallest substring in s that contains all characters of t.
Hint: Use sliding window and a hash map to count required characters.

• Approach: Sliding Window + Two Pointers

• Steps:

  1. Use two pointers left and right to define the current window.

  2. Maintain a hash map need for characters in t and their counts.

  3. Expand right to include characters until the window satisfies all t characters.

  4. Contract left to remove extra characters while still satisfying the condition, updating min window.

  5. Repeat until right reaches the end of s.

• Complexity:

  • Time: O(|S| + |T|)

  • Space: O(|T|) for the hash map

• Pattern Reminder:

  • Sliding window + character frequency counting

  • Often used for substring/interval problems with constraints

from collections import Counter

def minWindow(s: str, t: str) -> str:

if not s or not t:

return ""

need = Counter(t)

window = {}

have, need_count = 0, len(need)

res, res_len = [0,0], float('inf')

l = 0

for r, char in enumerate(s):

window[char] = window.get(char, 0) + 1

if char in need and window[char] == need[char]:

have += 1

while have == need_count:

# update result

if r - l + 1 < res_len:

res = [l, r]

res_len = r - l + 1

# shrink window

window[s[l]] -= 1

if s[l] in need and window[s[l]] < need[s[l]]:

have -= 1

l += 1

l, r = res

return s[l:r+1] if res_len != float('inf') else ""

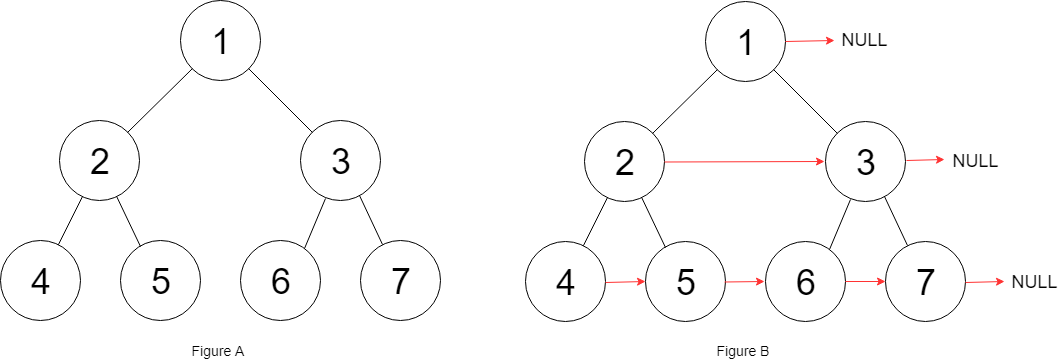
116. Populating Next Right Pointers in Each Node
You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

💡 Back (Answer / Key Idea + Code)

Idea:

• Traverse the tree level by level.

• Use existing next pointers to connect the next level’s nodes.

• Each node’s left.next = right, and if node.next exists, then right.next = node.next.left.
  
  Complexity:

  • ⏱ Time: O(n)

  • 💾 Space: O(1)

Q: What technique is used in moveZeroes problem?

Two-pointer technique (in-place array reordering).
Key Idea: Move non-zero elements forward with pointer i while scanning with pointer j.
Complexity: O(n) time, O(1) space.

Q: How do you rotate a square matrix 90 degrees clockwise in-place?
Explain the intuition and provide Python code.

A:
Use the transpose + reverse technique.

1. Transpose the matrix → swap elements across the diagonal.

2. Reverse each row → gives the 90° clockwise rotation.

Q:
How do you rotate a square matrix 90° clockwise and counterclockwise in-place?
Explain both methods, their key steps, and the difference between them.

🔹 Goal

Rotate a matrix in-place (O(1) space, O(n²) time).

---

🔸 1. 90° Clockwise Rotation

Key Idea:
➡ Transpose, then reverse each row

Steps:

1. Transpose: swap matrix[i][j] with matrix[j][i].
   (Converts rows into columns.)

2. Reverse each row: flips elements horizontally → rotates right.

2. 90° Counterclockwise Rotation

Key Idea:
⬅ Either:

• Transpose, then reverse columns, or

• Reverse rows, then transpose

Steps (simpler version):

1. Reverse the order of rows (flips vertically).

2. Transpose → swaps rows with columns → rotates left.

73. Set Matrix Zeroes
Given an m x n integer matrix matrix, if an element is 0, set its entire row and column to 0's.

Q: What is the O(MxN) complexity and O(1) space algo?

• Check if first row or first column originally contain 0.

• Traverse the rest of the matrix. For every matrix[i][j] == 0, mark matrix[i][0] and matrix[0][j] as 0.

• Zero out rows based on first-column markers.

• Zero out columns based on first-row markers.

• Finally, if first_row_zero or first_col_zero is True, zero out the entire first row or column.

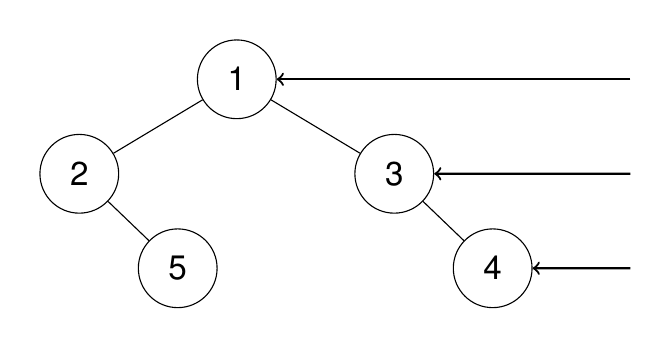
199. Binary Tree Right Side View
Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.

    def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
        if not root:
            return []

        ret = []

        def dfs(root:Optional[TreeNode],depth:int)-> None:
            if not root:
                return
            if depth == len(ret):
                ret.append(root.val)
            
            dfs(root.right,depth+1)
            dfs(root.left,depth+1)            

        dfs(root,0)
        return ret

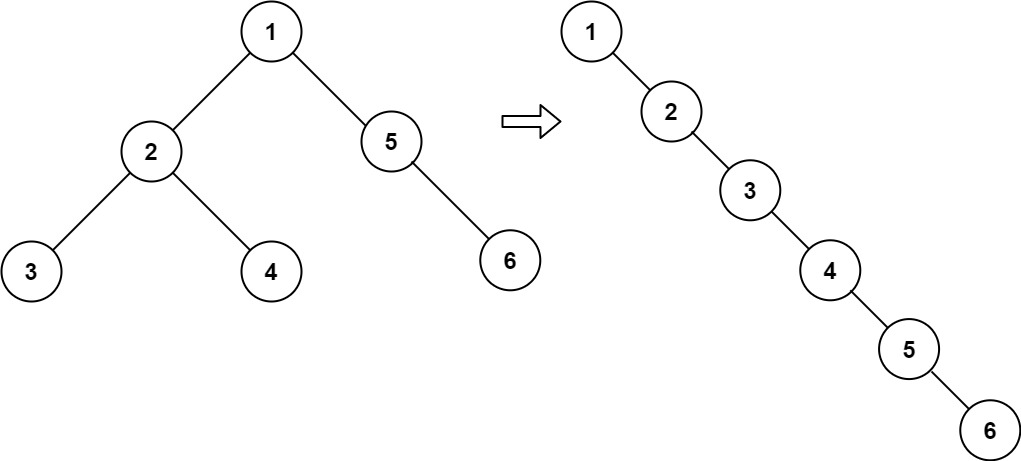
Flatten a binary tree to a linked list in-place following preorder traversal.

• Transform the tree so that all nodes appear along the right child pointers only.

• Do not return anything; modify the original tree.

A:1. Iterative Stack-Based Solution (O(N) time, O(H) space)

Idea:

• Use a stack to simulate preorder traversal.

• Always process the current node:

  1. If there is a right child, push it onto the stack.

  2. If there is a left child, push it onto the stack.

• Pop the next node from the stack and set it as current.right.

• Set current.left = None.
  
  
  

  class Solution:
      def flatten(self, root: Optional[TreeNode]) -> None:
          if not root:
              return
          
          stack = [root]
          
          while stack:
              node = stack.pop()
              
              if node.right:
                  stack.append(node.right)
              if node.left:
                  stack.append(node.left)
              
              if stack:
                  node.right = stack[-1]  # next node in preorder
              node.left = None
  

746. Min Cost Climbing Stairs
You are given an integer array cost where cost[i] is the cost of ith step on a staircase. Once you pay the cost, you can either climb one or two steps.

You can either start from the step with index 0, or the step with index 1.

Return the minimum cost to reach the top of the floor.

   

def v1() ->int:
    dp = [0] *(len(cost)+1)
    n = len(cost)

    for i in range(2,n+1):
        dp[i] =   min(dp[i-1] + cost[i-1],dp[i-2]+ cost[i-2])
    
	return dp[n]

   

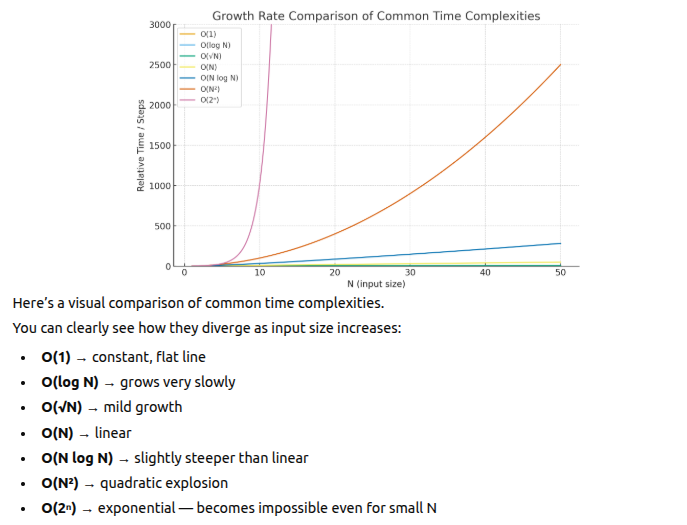
Big O

O(1) < O(log N) < O(√N) < O(N) < O(N log N) < O(N²) < O(2^N)

#739 daily temps (monotonic stack)

Given an array of integers temperatures represents the daily temperatures, return an array answer such that answer[i] is the number of days you have to wait after the ith day to get a warmer temperature. If there is no future day for which this is possible, keep answer[i] == 0 instead.

   def dailyTemperatures(self, temperatures: List[int]) -> List[int]:

        answers = [0]*len(temperatures)
        s = []

        for i, t in enumerate(temperatures):
            # print(s)
            while s and temperatures[s[-1]] < t:
                idx = s.pop()
                answers[idx] = i - idx
            
            s.append(i) 

        return answers

Word Ladder #127 Hard
A transformation sequence from word beginWord to word endWord using a dictionary wordList is a sequence of words beginWord -> s1 -> s2 -> ... -> sk such that:

• Every adjacent pair of words differs by a single letter.

• Every si for 1 <= i <= k is in wordList. Note that beginWord does not need to be in wordList.

• sk == endWord

Given two words, beginWord and endWord, and a dictionary wordList, return the number of words in the shortest transformation sequence from beginWord to endWord, or 0 if no such sequence exists.

1. Prepare graph 

for w in wordList:
  for i in range(len(w)):
    p=w[:i] +”*” +w[i+1:]
    g=g.get(p,[]) + [w]

2. Do BFS starting with beginWord 

q = [(beginWord,1)]

while q : 
  #do BFS 
  cur,depth = q.pop(0)
  if cur = endWord:
    return depth #FOUND !!!