Pure year 2 notes

Chapter 3

Chapter 3

What do a, d, L and n represent in arithmetic sequences?

a = first term

d = common difference

L = last term

n = number of terms

What is the nth term of an arithmetic sequence given by?

a + (n-1)d

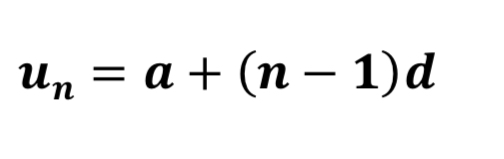
What are the two ways to find the sum of an arithmetic series?

When you don’t know the last term = n/2[2a+(n-1)d]

When you know the last term = n/2(a+l)

Proving the sum of an arithmetic series

1. List out Sn frontways

2. List out Sn backways

3. Add them together to get 2Sn

4. 2Sn = n x (2a + (n-1)d)

5. Divide by 2 to get the formula.

Proving the sum of a geometric series

1. List out Sn of a geometric sequence (a + ar + ar² +…ar^n-1)

2. List out rSn (multiply by r)

3. Sn - rSn = a - ar^n (take away rSn and show cancelling out)

4. Factorise both sides (taking out Sn and a) to get Sn(1 - r) = a(1 - r^n)

5. Rearrange by dividing by (1 - r)

What is the nth term of a geometric sequence?

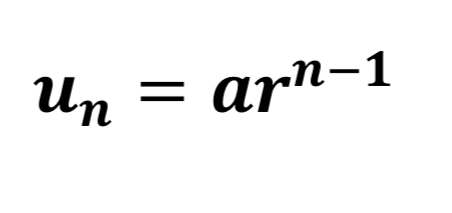
What are the two ways to find the sum of a geometric series?

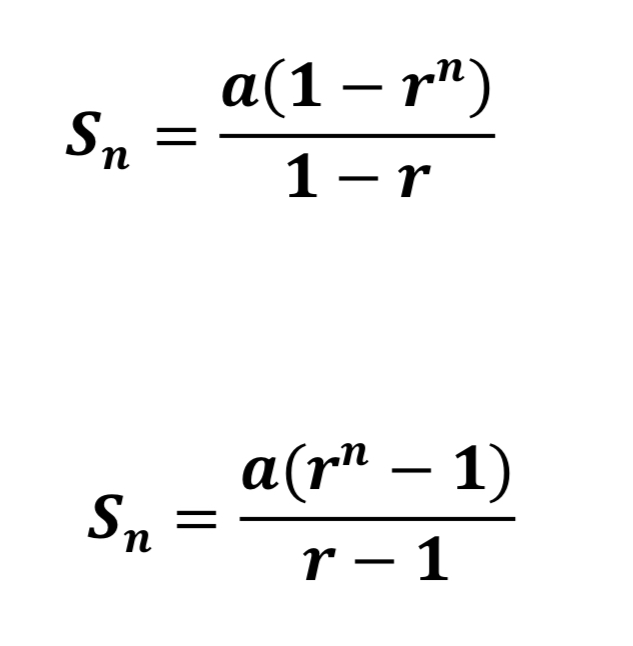
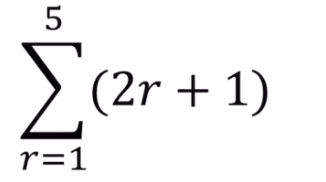
Sigma notation

Start with substituting the term at the bottom (1) and keep substituting higher and higher until you get to 5.

Chapter 4

Chapter 4

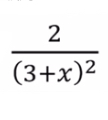
How would you start off a binomial expansion of this expression?

2(3+x)^-2 = 2 × 3^-2(1+x/3)^-2

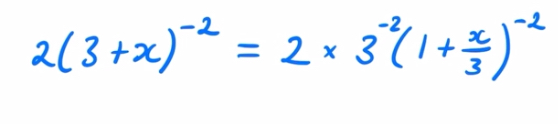
Chapter 5

Chapter 5

Important properties of sin and cos

sinx = sin(π-x)

cosx = cos(2π-x)

Chapter 6 and 7 trigonometric functions/modelling

Pythagorean identities

1 + tan²x ≡ sec²x (derived from dividing the OG by cos²x)

1 + cot²x ≡ cosec²x (derived from dividing the OG by sin²x)

Addition formulae (these are in formula booklet)

sin(A+B) = sinAcosB + cosAsinB, sin(A-B) = sinAcosB - cosAsinB

cos(A+B) = cosAcosB - sinAsinB, cos(A-B) = cosAcosB + sinAsinB

tan(A+B) = tanA+tanB/1 - tanAtanB, tan(A-B) = tanA - tanB/1 + tanAtanB

Express additions of sin and cos in the form Rsin(x+a) and Rcos(x-a). Example: 3sinx + 4cosx

1. Set up by equating both parts of the question. 3sinx + 4cosx = Rsin(x+a)

2. Use addition formulae. Rsin(x+a) = Rsinxcosa + Rcosxsina = 3sinx + 4cosx

3. Compare the coefficients to find that 3 = Rcosa and 4 = Rsina

4. Square both parts, factorise and use the identity (or simply use pythagoras)

5. Divide Rsina and Rcosa by each other to find tana, then find a

6. Put found values of R and a back into the equation

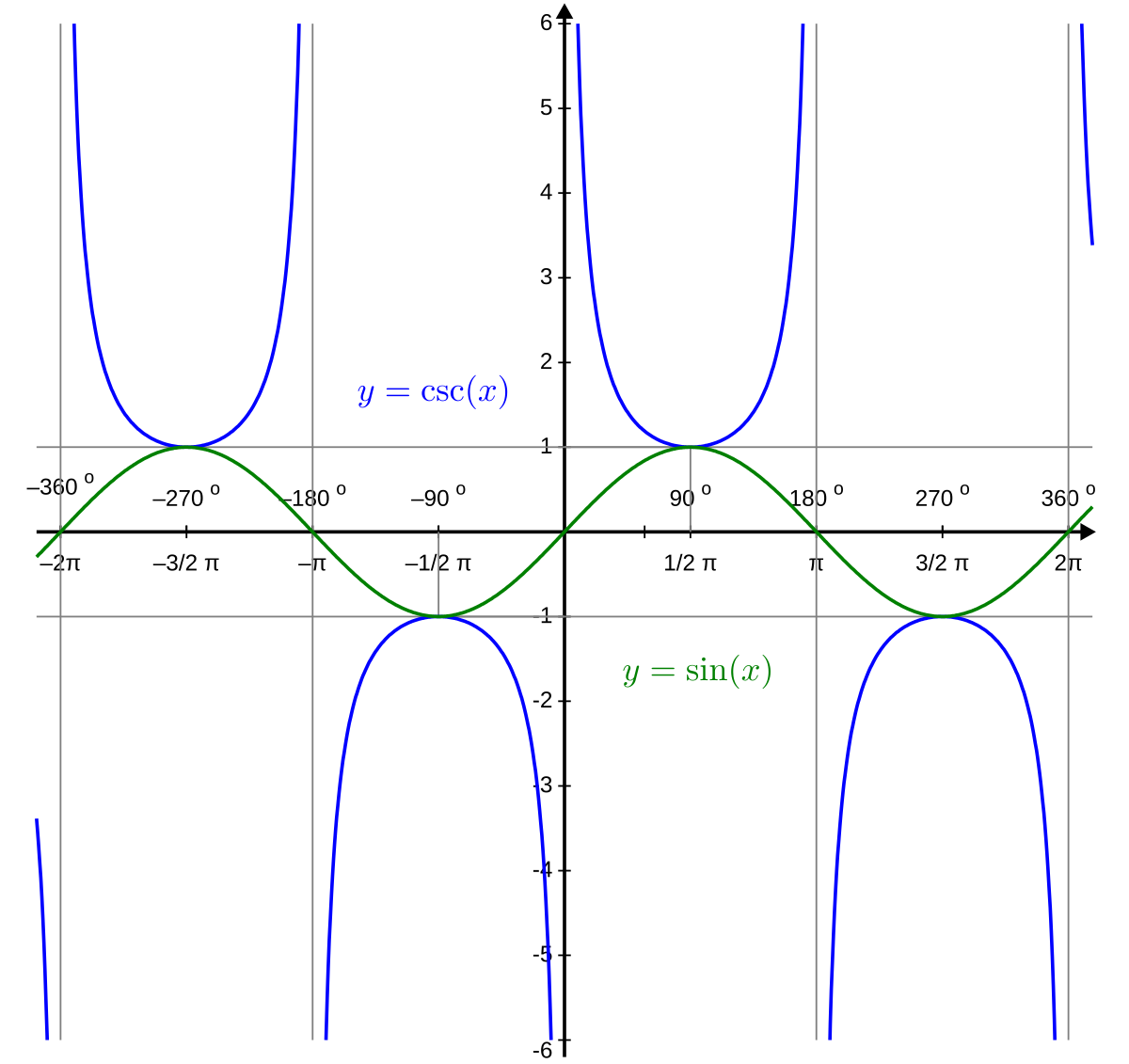
Graphs of cosecx and sinx

Sinx: max/min at 1/2pi, 3/2pi…x-intercepts at pi, 2pi…

Cosecx: graphs start at 1 and -1 (on y axis) and these are also 1/2pi, 3/2pi on x axis. Pi, 2pi, etc are asymptotes.

Double angle formulae

sin2x = 2sinxcosx

cos2x = cos²x - sin²x = 2cos²x - 1 = 1 - 2sin²x

tan2x = 2tanx/1 - tan²x

Remember that these can go both ways.

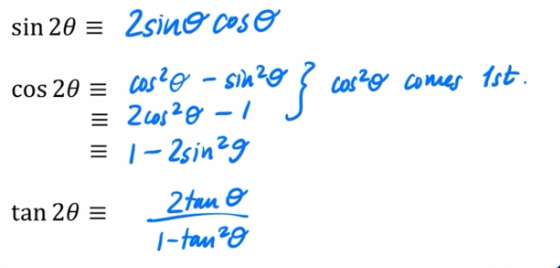
Domain and range for key functions

• y = x² (quadratic) → domain: any value, range: consider the turning point (min/max value)

• y = 2^x, e^x, etc. → domain: any value, range: y > 0 (only positive)

• y = ln(x) → domain: x > 0 (only positive), range: any value